Существует несколько основных типов распределения св, которые часто используются на практике. Рассмотрим их. Равномерное распределения св

Опр. Равномерным наз. распределение СВ , значения которых лежат на некотором отрезке [a,b] и имеют постоянную плотность вероятности h .

И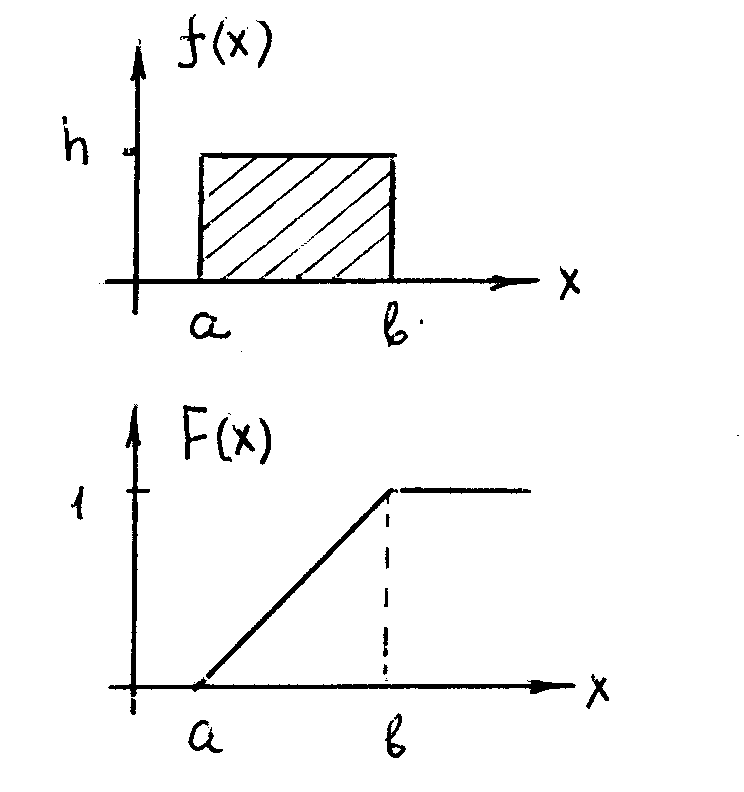 з условия нормировки: h(b – a) = 1 h = 1/(b – a),

f(x) = ; F(x) = (20)

МО: M(Х)= x f(x) dx = = , т.е. в центре распределения.

Дисперсия: D(X) = = - = (b – a)²/12

Среднее квадратичное отклонение = (b – a) / 2 .

В случае дискретных СВ Х = (х₁. х₂, . . . , х_n) вероятности p_i = 1/n

M(Х)= , D(X) = - ( )²

Пр.9. Все показания прибора между двумя соседними целочисленными значениями равновероятны. Они образуют непрерывные СВ на промежутке (0, 1). Найти характеристики такого распределения.

Решение. Из ( 20 ) f(x) = 1 ; F(x) = x , x [0,1) ; M(X) = ½ ; D(X) = 1/12 ; = 1 / 2

Биноминальный закон распределения

Пусть вероятность события А равна p и (1 - p)  q. При n повторных испытаниях А может произойти 0, 1, 2, . . . , n раз. Это случайные величины. Вероятность их появления определяет формула Бернулли

P_n(m) = C_n^m p^m q^{n – m} ( 7 )

Сочетание целочисленных СВ и вероятностей ( 7 ) наз. биноминальным законом распределения.

Вычислим M(Х) . Пусть X_i – число появлений события А при i – ом испытании. Это СВ со следующим распределением

Xi	0	1
pi	q	p

M(X_i) = 0q + 1p = p , но X = X₁ + . . .+ X_n и M(Х) = = np . Найдем D(X) и . Распределения и математические ожидания для X_i² и X_i совпадают. M(X²_i) = 0²q + 1²p = p. Поэтому D(X_i ) = M(X²_i) - M²(X_i ) = = p – p² = p(1 – p) = pq и D(X) = = n p q. Отсюда = .

Локальная предельная теорема Лапласа

позволяет при больших n вычисление P_n(m) проводить по приближенной формуле

P_n(m) ( 21 )

где . Значения определяют из таблиц. Интеграл от этой функции в пределах от до определяет P_n(k,l) – вероятность того, что событие А при n испытаниях появится не менее k раз и не более l раз. Первообразной для служит функция Лапласа или интеграл вероятностей

( 22 )

Интегральную предельную теорему Лапласа теперь можно представить в виде

P_n(k,l) – ( 23 )

Функция Лапласа вычисляют по таблицам , = 0 и она нечетная

= = - после замены: t= -z, dt= -dz

Пр. Вероятность того, что изделие не прошло проверку ОТК, равно 0,2. Найти вероятность того, что среди 400 изделий непроверенными окажутся от 70 до 100 изделий.

Решение. Имеем n = 400 , k = 70 , l = 100, p = 0,2 , q = 0,8 ,

тогда = = - 1,25 , = = 2,5 ,

P₄₀₀(70,100) = - = + = 0,4938 + 0,3944 = 0,8882