
- •Основные понятия теории вероятностей
- •Случайные события
- •Вероятность случайных событий
- •Сложение и умножение вероятностей
- •Формула Бернулли
- •Случайные величины
- •Числовые характеристики св
- •Существует несколько основных типов распределения св, которые часто используются на практике. Рассмотрим их. Равномерное распределения св
- •Биноминальный закон распределения
- •Распределение Пуассона
- •Показательное распределение
- •Нормальное распределение (распределение Гаусса)
- •Элементы математической статистики Основные понятия математической статистики
- •Оценки параметров распределения
- •Доверительный интервал
- •Доверительный интервал нормального распределения
- •Проверка статистических гипотез
- •Устные экзаменационные вопросы
Числовые характеристики св
СВ ( 10 ) занимают некоторую область числовой оси Ох. Такую область удобно описывать положением её центра и средним отклонением xi от этого центра.
Пр. Пятно от выстрелов на мишени имеет центр и круг около него некоторого радиуса, который охватывает большую часть попаданий. Это два наглядных параметра распределения.
Опр. Математическим ожиданием M(Х) дискретной СВ наз. сумма произведений всех ее возможных значений xi на их вероятности pi
M(Х)
=
![]() (
14 )
(
14 )
M(Х) – взвешенное среднеарифметическое значение СВ или просто среднее значение СВ в рамках статистической модели
хср
=
![]() x1
p1
+ x2
p2
+ . . . + xk
pk
x1
p1
+ x2
p2
+ . . . + xk
pk
Общие свойства M(Х): 10 M(С) = C, т.к. M(С) = С 1= С ; 20 M(СХ) = C M(Х);
30 M(Х+Y) = M(X) + M(Y); 40 M(ХY) = M(Х) M(Y); 50 M(Х-Y) = M(Х) - M(Y), где X , Y - независимые СВ.
Отклонения дискретных СВ от M(Х) описывает закон распределения
X – M(Х) |
x1– M(Х) |
x2– M(Х) |
. . . . |
xn– M(Х) |
P |
p1 |
p2 |
. . . . |
pn |
Вычислим для них математическое ожидание. Согласно свойств 10 , 50 имеем M[X – M(Х)] = M(Х) – M(Х) = 0 , т.к. отклонения имеют разные знаки. Приходится записывать закон распределения для квадратов отклонений
(X –M(Х))2 |
(x1– M(Х))2 |
(x2– M(Х))2 |
. . . . |
(xn– M(Х))2 |
P |
p1 |
p2 |
. . . . |
pn |
Опр. Дисперсией СВ наз. МО квадрата отклонения СВ от ее МО
D(X) = M{[X – M(Х)]2} ( 15 )
Дисперсия СВ есть
мера рассеяния ее значений около МО.
Если M(Х)
![]() m,
то
m,
то
D(X)
=
![]() (
16 )
(
16 )
Общие свойства дисперсии :
10 D(X) = M { X2 - 2 X M(X) + M2(X) } = M(X2) - M2(X)
20 D(C) = M(C2) - M2(C ) = C2 - C2 = 0
30 D(CX) = M(C2X 2) - M2(CX) = C2M(X2) - C2M2(X) = C2 D(X)
40 D(X+Y) = M((X+Y)2) - M2(X+Y) = D(X) + D(Y)
50 D(X-Y) = M((X -Y)2) - M2(X -Y) = D(X) + D(Y)
Математическое ожидание (МО) непрерывных СВ определяется по формуле M(Х) = x f(x) dx ( 17 )
Интегральная сумма для ( 17 ) имеет вид ( 14 ) , где pi f(x)dx. Геометрический смысл интеграла ( 17 ) : он определяет xc - координату центра тяжести криволинейной трапеции от функции f(x). Если f(x) симметричная , то xc лежит на оси симметрии.
Дисперсия непрерывных СВ, соответственно, определяется формулой
D(X)
=
![]() (
18 )
(
18 )
или
D(X)
=
![]() - m2
(
18а
)
- m2
(
18а
)
Все общие свойства дисперсии сохраняются.
Опр. Среднее
квадратичное отклонение СВ
![]() определяется
как квадратный корень от дисперсии
определяется
как квадратный корень от дисперсии
![]() (
19 )
(
19 )
Оно задает размер ближайшей окрестности центра распределения СВ, которая охватывает основные взвешенные значения СВ. Вероятность попадание за пределы этой окрестности в серии испытаний незначительна.
Пр.8. Дана плотность
распределения f(x)
=
![]() .
.
Найти функцию
распределения F(x),
МО M(Х),
дисперсию
D(X),
,
вероятность P(![]() ).
Построить
графики.
).
Построить
графики.
Р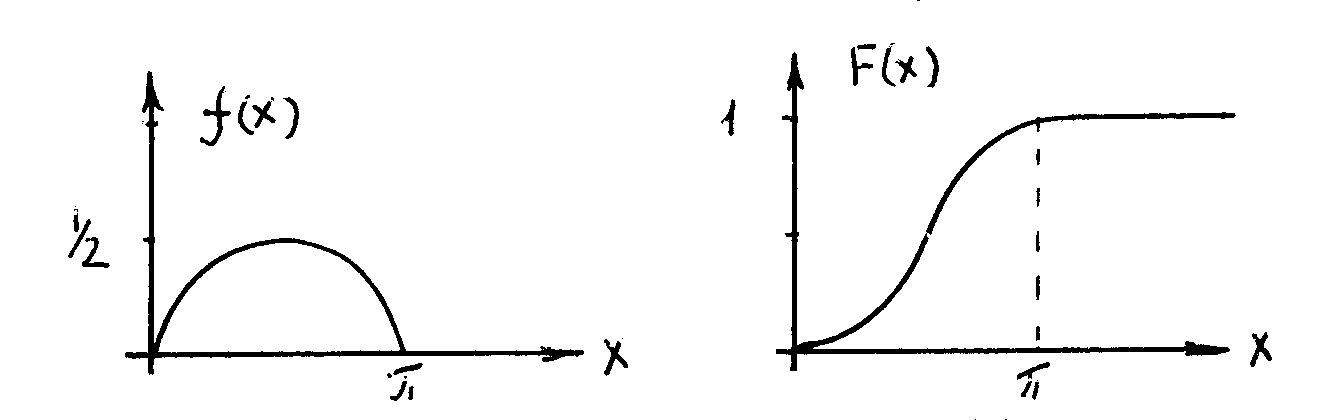 ешение.
Проверка нормировки
f(x)dx
=½
ешение.
Проверка нормировки
f(x)dx
=½![]() =
-½ cos
x
=
-½ cos
x![]() =1
=1
Функция распределения:
F(x)
=
f(x)dx
=

МО:
M(Х)
=
x
f(x)
dx
= ½
![]() = ½ [-x
cos
x
+
= ½ [-x
cos
x
+![]() ]=
]=
![]() /2
совпадает
с осью симметрии
f(x).
/2
совпадает
с осью симметрии
f(x).
Дисперсия
:
D(X)
=
![]() = ½
= ½![]() =
=
= ½
[-x2cos
x
+
2x
sin x
+ 2cos x]
-
![]() =
=
![]() .
.
Среднее квадратичное
отклонение
=
[![]() ]1/2
= 0,69
]1/2
= 0,69
Вероятность P(![]() )
= F(
)
= F(![]() )
= sin2(
/8)
)
= sin2(
/8)
Распределения случайных величин
