Формула Бернулли

Пусть вероятность события А : P(A) = p , а P( ) = q  1 – p . Проводим n независимых испытаний. Надо найти вероятность того, что при n испытаниях событие А произойдет m раз. Это событие В. P(B)  P_n(m) =?

Элементарное событие для В - произвольная последовательность из m событий А и (n–m) событий . Пусть B₁ = AA . . . A . . . , т.е. после n A следуют (n-m) . По теореме умножения ( 6 ) P(B₁) = p^m q^{n – m} . Остальные B_i получаются в результате распределения m событий А среди n мест и каждое имеют ту же вероятность. Выборка из n мест меньшего числа мест m, без учета порядка, есть сочетание. Т.о., число всех B_i , благоприятствующих В равно C_n^m и по теореме сложения вероятностей ( 2 )

P_n(m) = C_n^m p^m q^{n – m} ( 9 )

Эта формула Бернулли определяет вероятность появления одного события при повторных испытаниях.

Пр.7. Найти вероятность того, что в семье из пяти детей три девочки. Вероятности рождения мальчика и девочки одинаковы.

Решение: Событие А – рождение девочки, тогда Р(А) = p = ½ , P( ) = q = ½. Имеем схему испытаний Бернулли, где n = 5 , m = 3 , т.е. искомая вероятность равна P₅(3) = C₅³(1/2)³(1/2)² = (5! /3! 2!) (1/8)(1/4) = 5/16

Случайные величины

Случайному событию можно сопоставить некоторое число, которое будет служить численным параметром этого события. В результате, от рассмотрения самих случайных событий переходим к рассмотрению случайных величин.

Пр. Игральная кость. Случайное событие – выпадение определенной грани, случайная величина Х – число очков на этой грани.

Опр. Случайной величиной (СВ) наз. переменная Х , которая в результате испытания может принять одно, неизвестное заранее, значение.

СВ могут быть дискретными и непрерывными. СВ Х дискретна, если множество ее значений конечно Х = (х₁. х₂, . . . , х_n). Тогда она является элементарным событием с вероятностью p_i = P(x_i)

Опр. Законом распределения дискретных СВ Х наз. соответствие между возможными значениями х_i и их вероятностями p_i . Записывается в виде таблицы

X	x1	x2	x3	…	xn
P	p1	p2	p3	…	pn

( 10 )

В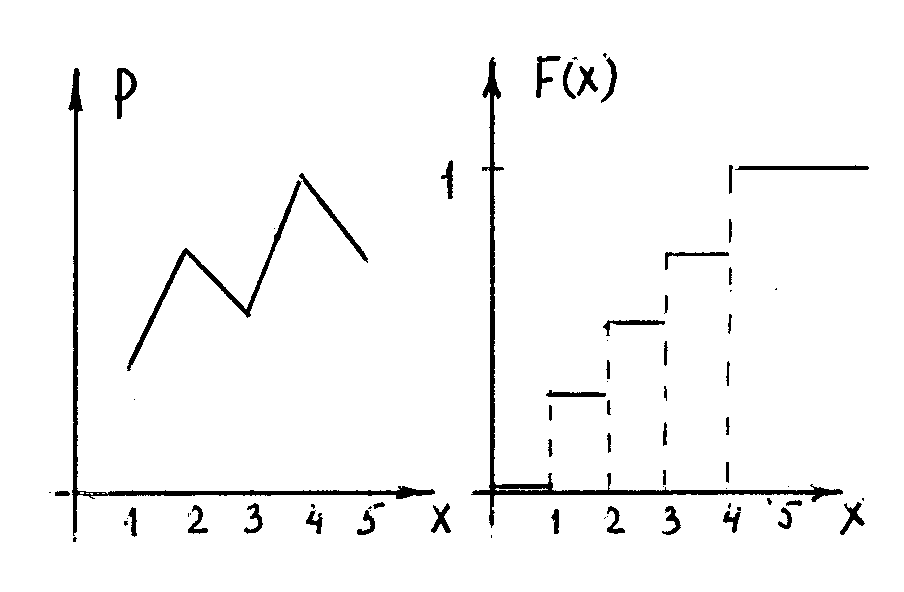 системе координат хОр таблице ( 10 ) соответствуют n точек или многоугольник распределения, составленный из прямых, соединяющих соседние точки. Согласно теореме сложения вероятностей ( 2 ), сумма

первых k величин p_i задает вероятность того, что СВ Х окажется в интервале от x₁ до x_k . Эта сумма  P(X<x_k)  F(x_k)

наз. функцией распределения вероятностей. Она кусочно-непрерывна, ей соответствует ступенчатая фигура, которая возрастает скачками от 0 при х < x₁ до 1 при х  x_n . Функция распределения удобна для вычисления вероятности появления СВ на любом промежутке числовой оси (a, b):

P(X<b) – P(X<a)  P(a<x<b) = F(b) – F(a)

Непрерывная СВ Х может принимать все значения на некотором промежутке оси ОХ Х (a, b). Однако, вероятность появления конкретного числа х равна нулю, т.к. m/n = 1/ = 0 . Вероятность появления числа из окрестности х уже не 0, а отношение двух бесконечно больших чисел: m/n = /  0 . Эта вероятность пропорциональна величине выбранного интервала (x-,x+), но коэффициент пропорциональности в разных точках оси может быть различен.

Опр. Функцией распределения СВ Х наз. непрерывная, дифференцируемая функция F(x) = P(X<x), которая равна нормированной вероятности того, что СВ примет значение меньшее х.

Свойства функции F(x):

1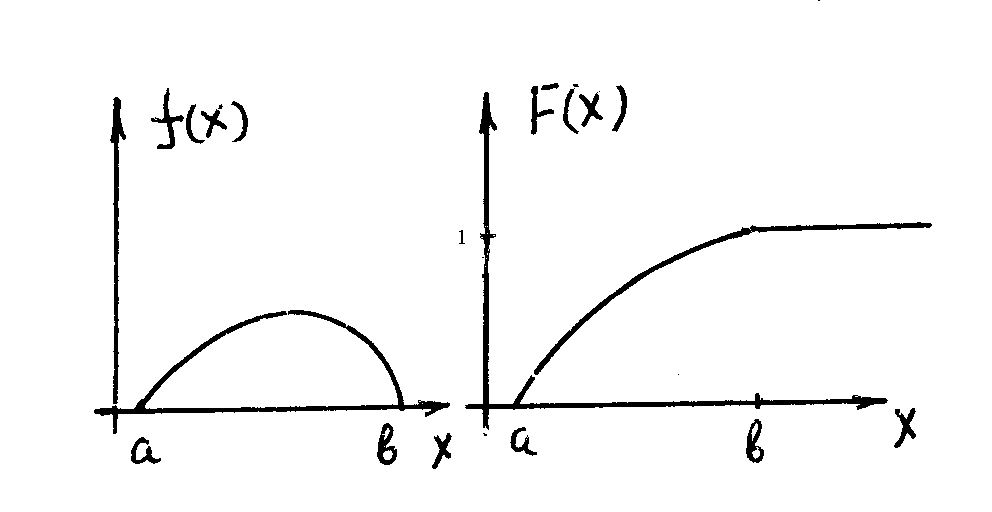 ⁰ limF(x)= ; 2⁰ F(x₁)< F(x₂), если x₁ < x₂ . Производная F`(x) = f(x) наз. плотностью распределения вероятности. Она служит коэффициент пропорциональности между приращением функции и приращением аргумента dF = f(x) dx . Cвязь между ними можно записать и в виде интеграла

F(x) = f(x) dx ( 11 )

Т.о. функция распределения F(x) определяется площадью криволинейной трапеции, форму которой задает функция f(x). В силу 1⁰

f(x) dx = 1 ( 12 )

т.е. площадь графика функции f(x) нормирована на 1 . Вероятность того, что СВ попадет в заданный промежуток (a,b) равна интегралу

P(a< X < b) = F(b) - F(a) = f(x)dx ( 13 )