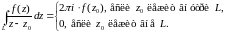Вопрос №1 Необходимые и достаточные условия дифференцируемости функции комплексной переменной
Теорема
3. Пусть
функция
 определена в некоторой области G.
Для того, чтобы функция f(z)
была дифференцируемой в точке z
области G
необходимо и достаточно, чтобы
определена в некоторой области G.
Для того, чтобы функция f(z)
была дифференцируемой в точке z
области G
необходимо и достаточно, чтобы
функции u(x;y) и v(x;y) были дифференцируемы в точке z как функции двух действительных переменных;
в точке z выполнялись равенства
 и
и
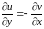 . (1)
. (1)
При выполнении всех условий теоремы производная может быть представлена в одном из следующих видов:
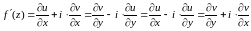 . (2)
. (2)
Равенства (1) называются условиями Коши-Римана (или Даламбера-Эйлера).
Доказательство.
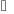 1)
Необходимость.
1)
Необходимость.
Пусть функция f(z) дифференцируема в точке z области G. Тогда по теореме 1 ее приращение может быть представлено в виде
 ,
где
,
где
 .
.
 -
комплексная функция от z.
Следовательно,
-
комплексная функция от z.
Следовательно,
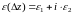 ,
где
,
где
 .
.
 -
комплексное
число,
значит,
-
комплексное
число,
значит,
 ,
a,b
,
a,b .
Тогда
.
Тогда
f(z)=u+iv=(a+ib)(x+iy)+(1+i2)(x+iy)=ax-by+i(ay+bx)+
+1x-2y+i(1y+2x)=(ax-by+1x-2y)+i(ay+bx+1y+2x).
Отсюда
u=ax-by+1x-2y,
v=bx+ay+2x+1y, где . (3)
Из (3) следует, что
1) функции u(x;y) и v(x;y) дифференцируемы в точке (x;y),
2) их частные производные в точке (x;y):
 ,
,
 ,
,
 ,
,
 .
.
Отсюда , , т.е. удовлетворяют условиям Коши-Римана.
Тогда для производной получаем:
 .
.
2) Достаточность.
Пусть в точке z области G выполнены условия 1) и 2) теоремы. Придадим точке z=(x;y) приращение z=x+iy0. По условию
 где
где
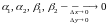 . (4)
. (4)
Приращение
функции
 ,
соответствующее приращению
,
соответствующее приращению
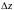 ,
имеет вид:
,
имеет вид:
 .
Разделим на
:
.
Разделим на
:
 .
Используя условия Коши-Римана, перейдём
к частным производным по x:
.
Используя условия Коши-Римана, перейдём
к частным производным по x:
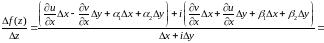
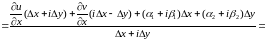
 . (5)
. (5)
Т.к.
 ,
,
 ,
и
,
и
 ,
то
,
то
 и
и
 (огр.БМФ).
(огр.БМФ).
Следовательно,
переходя в (5) к
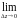 ,
получим:
,
получим:
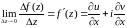 ,
т.е. f(z)
дифференцируема в точке z.
,
т.е. f(z)
дифференцируема в точке z.

Формулами (2) можно пользоваться для вычисления производных.
Вопрос №2 Понятие функции аналитической в точке и области. Гарм. функции. Необх. и достат. условие.
Определение.
Функция f(z)
называется аналитической
(голоморфной,
регулярной,
правильной)
в точке
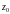 ,
если она дифференцируема в каждой точке
некоторой окрестности точки
.
,
если она дифференцируема в каждой точке
некоторой окрестности точки
.
Заметим, что необходимо различать понятие дифференцируемости в точке и понятие аналитичности в точке:
f(z)
дифференцируема в точке
 ,
,
f(z)
аналитическая в точке

Определение. Функция f(z) называется аналитической в области G, если она дифференцируема в каждой точке этой области. Т.е. понятия дифференцируемости и аналитичности в области совпадают.
Примеры.
1)
 - аналитическая на
- аналитическая на
 .
.
2)
 аналитическая
на
.
аналитическая
на
.
3)
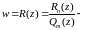 аналитическая
на
аналитическая
на
 .
.
4)
 нигде
не является аналитической, так производная
существует только в точке
нигде
не является аналитической, так производная
существует только в точке
 (см. пример 2 п.2).
(см. пример 2 п.2).
Гармонические функции
Определение.
Дифференциальное уравнение с частными
производными второго порядка
 называется уравнением
Лапласа.
называется уравнением
Лапласа.
Обозначим
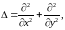 тогда
тогда
 -краткая
запись уравнения Лапласа.
-краткая
запись уравнения Лапласа.
Определение. Действительная функция двух действительных переменных называется гармонической на области G, если она имеет непрерывные частные производные второго порядка и на G удовлетворяет уравнению Лапласа.
Определение. Две гармонические функции, связанные условиями Коши – Римана, называются сопряжёнными гармоническими функциями.
Позже будет доказано, что производная аналитической функции сама является аналитической функцией. Используем этот факт при доказательстве следующей теоремы.
Теорема 5. Для того чтобы функция f(z)=u(x,y)+iv(x,y) была аналитической в области G необходимо и достаточно, чтобы её действительная и мнимая часть были сопряжёнными гармоническими функциями.
Доказательство.
 1)
1)
 Пусть
f(z)=u(x,y)+iv(x,y)
аналитическая в некоторой области G.
Тогда по теореме 2 u(x,y)
и v(x,y)-дифференцируемые
функции двух действительных переменных
и удовлетворяют условиям Коши – Римана:
Пусть
f(z)=u(x,y)+iv(x,y)
аналитическая в некоторой области G.
Тогда по теореме 2 u(x,y)
и v(x,y)-дифференцируемые
функции двух действительных переменных
и удовлетворяют условиям Коши – Римана:
 .
.
Производная может быть представлена в одном из видов:
 или
или
 .
.
Так
как производная аналитической функции
является аналитической функцией, то
 и
и
 тоже дифференцируемые функции двух
действительных переменных и удовлетворяют
условиям Коши – Римана.
тоже дифференцируемые функции двух
действительных переменных и удовлетворяют
условиям Коши – Римана.
Применим
к паре функций
 и
и
 первое условие Коши– Римана, а для
функций
и
первое условие Коши– Римана, а для
функций
и
 - второе:
- второе:
 ,
,  ,
,
 , (7)
, (7)  , (8)
, (8)
т.е. u и v удовлетворяют уравнению Лапласа.
Покажем,
что u(x,y)
и v(x,y)
имеют непрерывные частные производные
второго порядка. Т.к. f(z)
- аналитическая функция, то
 -тоже
аналитическая функция.
-тоже
аналитическая функция.
Дифференцируя
 по x,
получим
по x,
получим
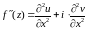 .
.
Из
(7), (8) .
.
Дифференцируя
 по y,
получим
по y,
получим
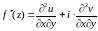 ,
,
т.е.
 является аналитической функцией и может
быть представлена в одном из видов:
является аналитической функцией и может
быть представлена в одном из видов:
 .
.
Значит, все частные производные второго порядка являются (по теореме 2) дифференцируемыми в области G функциями, следовательно, они непрерывны.
Итак, u(x,y) и v(x,y) имеют в G непрерывные частные производные второго порядка, удовлетворяют уравнению Лапласа и условиям Коши – Римана. Значит, они являются сопряжёнными гармоническими функциями.
2.
 Пусть
u(x,y)
и v(x,y)
какие – либо сопряжённые гармонические
в области G
функции. Так как они дифференцируемы и
удовлетворяют условиям Коши – Римана,
то по теореме 2 функция f(z)=u(x,y)+iv(x,y)
является дифференцируемой в G
и, следовательно, она аналитическая в
G.
Пусть
u(x,y)
и v(x,y)
какие – либо сопряжённые гармонические
в области G
функции. Так как они дифференцируемы и
удовлетворяют условиям Коши – Римана,
то по теореме 2 функция f(z)=u(x,y)+iv(x,y)
является дифференцируемой в G
и, следовательно, она аналитическая в
G.
 .
.
Из теоремы 5 следует, что действительной или мнимой частью аналитической функции может быть только гармоническая функция.
Например,
не существует аналитической функции
f(z),
у которой
 Действительно,
функция
Действительно,
функция
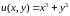 не является гармонической ни в какой
области G.
не является гармонической ни в какой
области G.
 ,
,  ,
, 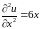 ,
,  .
.
 .
Следовательно,
.
Следовательно,
 только
на прямой
только
на прямой
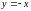 (не
является областью). Значит, u(x,y)
не является гармонической ни в какой
области G
из
.
(не
является областью). Значит, u(x,y)
не является гармонической ни в какой
области G
из
.
Вопрос №3. Теорема о восстановление аналитической функции по заданной действительной или мнимой части
Теорема 6. Для заданной функции u(x,y), гармонической в односвязной области G, существует бесконечное множество аналитических в G функций, действительной частью которых является u(x,y). Все они выражаются формулой

и
отличаются между собой на чисто мнимую
постоянную
 .
.
Доказательство.
Пусть дана гармоническая функция u(x,y). Для нахождения аналитической функции f(z)=u(x,y)+iv(x,y) необходимо найти мнимую часть v(x,y), которая дифференцируема в G и связана с u(x,y) условиями Коши – Римана:
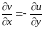 ,
, 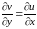 .
.
Так как u(x,y) известна, то известны её частные производные. Обозначим
 ,
, 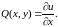
Тогда условия Коши – Римана запишутся в виде:

 . (9)
. (9)
Т.к.
u
гармоническая функция, то она имеет
непрерывные производные второго порядка,
следовательно, существуют

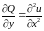 и
и
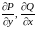
 непрерывны в G.
Тогда уравнение Лапласа для функции u
примет вид
непрерывны в G.
Тогда уравнение Лапласа для функции u
примет вид
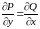 . (10)
. (10)
Т.к. непрерывны в G и удовлетворяют условию (10), то выражение P(x,y)dx+Q(x,y)dy является полным дифференциалом некоторой функции v0(x,y):
dv0(x,y)=P(x,y)dx+Q(x,y)dy
и
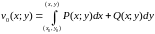 ,
,
где
интеграл по кривой, соединяющий точки
(x0,y0)
и (x,y)
в
,
не зависит от пути интегрирования. Имеем

 .
Надо найти функцию v(x,y)
удовлетворяющую условиям (9). Следовательно,
.
Надо найти функцию v(x,y)
удовлетворяющую условиям (9). Следовательно,
 .
.
Учитывая обозначения, получим
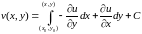 . (11)
. (11)
Следовательно, функция f(z)= u(x,y)+iv(x,y), где v(x,y) определяется соотношением (11), является аналитической функцией (u и v-дифференцируемы и связаны условиями Коши-Римана). Итак, .
Аналогично
можно показать, что для любой функции
v(x,y),
гармонической на области G
существует аналитическая в G
функция f(z)=u(x,y)+iv(x,y),
мнимая часть которой равна v(x,y).
Эта функция определяется с точностью
до постоянного слагаемого
 .
.
Вопрос №4. Линейная и дробно-линейная функция комплексного переменного. Свойства.
Определение.
Линейной
функцией
называется функция вида  , (1)
, (1)
где а, b- комплексные постоянные.
Эта
функция определена
 ,
,
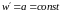 .
Следовательно, если
.
Следовательно, если
 ,то
линейная функция производит конформное
отображение всей плоскости комплексного
переменного. При этом касательные ко
всем кривым поворачиваются на один и
тот же угол Arga,
а растяжение во всех точках равно
,то
линейная функция производит конформное
отображение всей плоскости комплексного
переменного. При этом касательные ко
всем кривым поворачиваются на один и
тот же угол Arga,
а растяжение во всех точках равно
 .
Если a=1,
то
.
Если a=1,
то
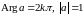 ,
значит, растяжение и поворот отсутствуют.
В этом случае получаем w=z+b.
Это отображение осуществляет сдвиг
всей плоскости на вектор
,
значит, растяжение и поворот отсутствуют.
В этом случае получаем w=z+b.
Это отображение осуществляет сдвиг
всей плоскости на вектор
 .
.
В
общем случае, переходя к показательной
форме записи комплексного числа
 ,
получим
,
получим
 .
Следовательно, линейное отображение
является композицией трех геометрических
преобразований:
.
Следовательно, линейное отображение
является композицией трех геометрических
преобразований:
 -
поворот на угол
-
поворот на угол
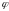 вокруг точки О;
вокруг точки О;
 -
подобие с коэффициентом r;
-
подобие с коэффициентом r;
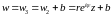 -
параллельный перенос на вектор
.
-
параллельный перенос на вектор
.
Подойдем
с другой стороны. Найдем число с,
такое что
 .
Отсюда, т.к.
,
то
.
Отсюда, т.к.
,
то

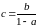 .
Значит, при
.
Значит, при
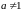 (и
)
отображение (1) сводится к повороту всей
плоскости вокруг точки
на угол
(и
)
отображение (1) сводится к повороту всей
плоскости вокруг точки
на угол
 с последующим растяжением относительно
этой точки в
раз, (т.е. подобие с центром в точке
и коэффициентом подобия
).
с последующим растяжением относительно
этой точки в
раз, (т.е. подобие с центром в точке
и коэффициентом подобия
).
Дробно-линейная функция
Рассмотрим
функцию вида
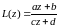 , (2)
, (2)
где a,b,c,d- комплексные числа.
Если
 ,
то получаем
,
то получаем
 -линейную
функцию.
-линейную
функцию.
Если
 ,
выделим в дроби целую часть
,
выделим в дроби целую часть
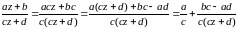 .
.
Если
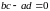 ,то
получаем, что
,то
получаем, что
 .
В дальнейшем будем считать, что
,
.
В дальнейшем будем считать, что
,
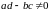 .
.
Определение. Функция вида (2), где a, b, c, d - комплексные числа, такие что , , называется дробно-линейной.
Свойства дробно-линейного преобразования
1 Конформность
 .
.
 существует
во всех конечных точках комплексной
плоскости, кроме точки
существует
во всех конечных точках комплексной
плоскости, кроме точки
 и
и
 0
(т.к.
).
Функция
0
(т.к.
).
Функция
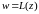 является
аналитической во всех конечных точках
плоскости, кроме
.
Следовательно, отображение
является конформным во всех конечных
точках к плоскости, кроме
.
является
аналитической во всех конечных точках
плоскости, кроме
.
Следовательно, отображение
является конформным во всех конечных
точках к плоскости, кроме
.
Т.к.
 ,
,  .
.
Таким
образом, функция
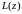 определена
на
определена
на
 .
.
Итак, дробно-линейная функция отображает взаимно однозначно и конформно расширенную комплексную плоскость саму на себя.
2 Круговое свойство.
Рассмотрим
астный случай
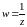 . (3).
. (3).
Положим
 ,
,
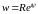 .Тогда
(3) примет вид
.Тогда
(3) примет вид

Следовательно,
отображение (3) разбивается на два
отображения. Сначала точка
 переходит в точку
переходит в точку
 .Т.к.
эти точки лежат на одном луче, выходящем
из начала координат и их модули связаны
соотношением
.Т.к.
эти точки лежат на одном луче, выходящем
из начала координат и их модули связаны
соотношением
 ,
то это преобразование инверсии
относительно единичной окружности.
Затем точка
переходит
в точку
,
то это преобразование инверсии
относительно единичной окружности.
Затем точка
переходит
в точку ,
симметричную ей относительно действительной
оси.
,
симметричную ей относительно действительной
оси.

Теорема. При отображении совокупность прямых и окружностей на комплексной плоскости переходит в себя.
Доказательство.
Уравнение для любой прямой или окружности имеет вид:
А(x2+y2)+2Bx+2Cy+D=0. (4)
При
А=0
и В,
С 0
одновременно это уравнение определяет
прямую, при А=0
и В2+С2
-AD>0
– окружность.
0
одновременно это уравнение определяет
прямую, при А=0
и В2+С2
-AD>0
– окружность.
Заменим 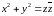 ,
, 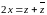 ,
,  , (5)
, (5)
получим
 .
.
Обозначим
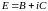 ,
тогда
,
тогда
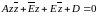 . (6)
. (6)
Если
А=0,
а Е0,
то уравнение (6) определяет прямую, если
А0
и ,
то окружность. Т.е. любая окружность или
прямая на комплексной плоскости
определяется уравнением (6).
,
то окружность. Т.е. любая окружность или
прямая на комплексной плоскости
определяется уравнением (6).
Верно и обратное: уравнение вида (6) определяет прямую или окружность на комплексной плоскости. Для доказательства надо в (6) сделать замену по формулам (5). Получим (4) , которое является уравнением либо прямой, либо окружности.
При
преобразовании
имеем
 .
Линия (6) перейдет в линию:
.
Линия (6) перейдет в линию:
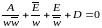

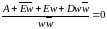
 . (7)
. (7)
Уравнение
(7) имеет тот же вид, что и (6), с заменой A
на D,
D
на А,
E
на
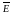 .
Следовательно, при D=0
– это уравнение прямой, а при
.
Следовательно, при D=0
– это уравнение прямой, а при
 -
уравнение окружности.
-
уравнение окружности.
Теорема 2. Образом прямой или окружности при дробно-линейном отображении w=L(z) является прямая или окружность, (причем образом прямой может быть как окружность, так и прямая, и образом окружности – как прямая, так и окружность).
Доказательство.
 .
.
Следовательно,
w=L(z)
является композицией трех отображений:
t=cz+d,
 ,
w=kq+l,
где
,
w=kq+l,
где
 ,
,
 .
Первое и третье - линейные отображения.
Они и отображение
переводят в себя совокупность прямых
и окружностей.
.
Первое и третье - линейные отображения.
Они и отображение
переводят в себя совокупность прямых
и окружностей.
Замечание. Несложно установить, что при отображении w=L(z) все прямые и окружности, проходящие через точку переходят в прямые плоскости (w), а все прямые или окружности, не проходящие через точку , - в окружности плоскости (w).
3 Инвариантность двойного отношения
Дробно-линейное
преобразование однозначно определяется
заданием трех параметров (например,
если с0,
то ими могут быть
 ).
Поэтому это отображение определяется
заданием образов трех точек. Выведем
формулу дробно-линейного преобразования.
).
Поэтому это отображение определяется
заданием образов трех точек. Выведем
формулу дробно-линейного преобразования.
Пусть
 ,
k=1,2,3.
Пусть
,
k=1,2,3.
Пусть
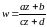 .
Образуем разности
.
Образуем разности


 ,
,
 ,
,  ,
,
 ,
, 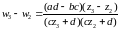 .
.
Разделим почленно первое уравнение на второе и третье и на четвертое.
 ,
,
 .
.
Разделим теперь снова первое уравнение на второе:
 . (8)
. (8)
Это и есть искомое линейное преобразование.
Т.к. за z1, z2, z3, z и w1, w2, w3, w могут быть приняты любые четверки точек, соответствующие друг другу при дробно-линейном преобразовании, то (8) выражает следующее свойство:
отношение
 сохраняется при дробно-линейном
отображении, т.е является его инвариантом.
Это отношение называется двойным
отношением четырех точек.
сохраняется при дробно-линейном
отображении, т.е является его инвариантом.
Это отношение называется двойным
отношением четырех точек.
4 Сохранение симметрии
Если
точки z1
и z2
симметричны относительно некоторой
прямой или окружности ,
то при любом дробно-линейном отображении
w=L(z)
их образы w1
и w2
будут симметричны относительно образа
:
 .
.
В случае, когда - окружность, преобразование называют инверсией.
5 Принцип соответствия обхода границ (отображение областей, ограниченных прямыми или окружностями)
Е сли
при дробно-линейном отображении прямая
или окружность
переходит в прямую или окружность
,то область D,
которую ограничивает ,
преобразуется в одну из двух областей,
которые ограничивает .
При этом имеет место принцип соответствия
обхода границ: если при каком-то обходе
линии
область D
оказывается слева (справа), то при
соответствующем
обходе линии
область D
тоже должна оказаться слева (справа).
сли
при дробно-линейном отображении прямая
или окружность
переходит в прямую или окружность
,то область D,
которую ограничивает ,
преобразуется в одну из двух областей,
которые ограничивает .
При этом имеет место принцип соответствия
обхода границ: если при каком-то обходе
линии
область D
оказывается слева (справа), то при
соответствующем
обходе линии
область D
тоже должна оказаться слева (справа).
Вопрос №5. Определение показательной функции и ее свойства.
Показательной
функцией комплексного переменного
называется
функция вида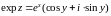 .
.
Свойства expz
1
Если
 ,
то expz=expx=ex,
т.е. на действительной оси показательная
функция комплексного переменного
совпадает с показательной функцией
действительного переменного.
,
то expz=expx=ex,
т.е. на действительной оси показательная
функция комплексного переменного
совпадает с показательной функцией
действительного переменного.
2

![]()

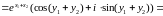
 .
.
С другой стороны,
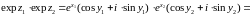
.
Следовательно,
.
![]()
Аналогичное
свойство имеет место для функции
действительного переменного:
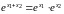 .
.
Назовём
комплексное число z
показателем
функции expz.
Следовательно, при перемножении двух
значений показательной функции показатели
можно складывать. В связи с этим можно
вместе с обозначением expz
использовать обозначение ez:  .
.
3
Из свойства 2
следует
 .
С другой стороны
.
С другой стороны
 .
Следовательно,
.
Следовательно,

 .
.
4
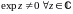 .
.
![]()
 .
.
Т.к.
 ,
то
.
,
то
.
![]()

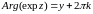 .
.
5 expz -периодическая функция с основным периодом 2i, т.е.
exp(z+2i)=expz.
![]()
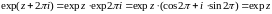 .
.
Покажем
что 2i
-основной период функции expz,
т.е. любой другой период имеет вид
2ki,где
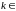
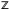 .
.
Действительно,
пусть
 -
период expz.
Тогда exp(z+w)=expz
z.
Значит и при z=0
это равенство выполнено.
-
период expz.
Тогда exp(z+w)=expz
z.
Значит и при z=0
это равенство выполнено.
Для
z=0:
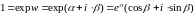 .
Отсюда
.
Отсюда
 что
и требовалось доказать.
что
и требовалось доказать.
![]()
6
Если
 так,
что
так,
что
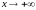 ,то
,то
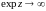 .
.
Если
так, что
 ,
то
,
то
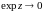 .
.
(6 следует из того, что ).
Выражение
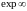 лишено смысла. Отсюда, в частности,
следует, что expz
не совпадает ни с одним многочленом
лишено смысла. Отсюда, в частности,
следует, что expz
не совпадает ни с одним многочленом
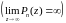 .
Целые функции, отличные от многочленов,
называются трансцендентными
целыми функциями.
Следовательно expz
- трансцендентная целая функция.
.
Целые функции, отличные от многочленов,
называются трансцендентными
целыми функциями.
Следовательно expz
- трансцендентная целая функция.
7 Показательная функция является аналитической на , (expz)=expz.
Вопрос №6. Тригонометрические функции. Гиперболические функции.
Т.
к.
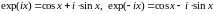 ,
то при сложении и вычитании соответственно
получим:
,
то при сложении и вычитании соответственно
получим:
 , (14)
, (14)
Формулы
(14) – формулы Эйлера, верные
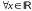 .
.
Если
 ,
то функции
,
то функции
 ,
,
 определены
и являются аналитическими, следовательно
они целые. При
определены
и являются аналитическими, следовательно
они целые. При
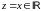 они принимают действительные значения,
совпадающие соответственно с cosx
и sinx.
Поэтому по определению первую обозначают
через cosz,
а вторую – sinz
и называют косинусом и синусом z.
они принимают действительные значения,
совпадающие соответственно с cosx
и sinx.
Поэтому по определению первую обозначают
через cosz,
а вторую – sinz
и называют косинусом и синусом z.
Определение.
 (15)
(15)
Формулы (15) тоже называются формулами Эйлера. Если вторую умножить на i и сложить с первой, то получим
 – (16)
– тоже формула Эйлера.
– (16)
– тоже формула Эйлера.
Свойства cosz и sinz
1 Из (15) следует cos(-z)=cosz, sin(-z)=sinz , следовательно cosz – чётная, sinz – нечётная.
2 cosz и sinz – периодические с периодом 2.
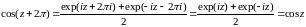 ,
,
т. к. 2i– основной период expz.

Покажем, что 2 – основной период cosz и sinz.
Пусть w – период cosz. Следовательно, cos(z+w)=cosz.
Если
 ,
то
,
то
 .
.
Следовательно,
 (по определению cosz).
(по определению cosz).
Отсюда
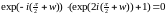
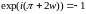 .
.
Тогда,
поскольку из expz=w
следует
 ,
то
,
то
 .
Значит w=k.
.
Значит w=k.
Если
z=0,
то
 (чётное число).
(чётное число).
Значит w=2m. Следовательно, 2 – основной период функции cosz.
Для sinz аналогично.
3 Для sinz и cosz справедливы основные формулы тригонометрии:
а) 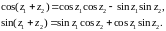 (17)
(17)
Заменяя
в (16) z
на
 ,
получим
,
получим

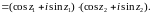
Следовательно,

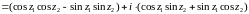 .
.
Заменяя здесь z1 и z2 на -z1 и -z2 и учитывая свойство 1, получим
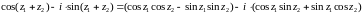 .
.
Складывая и вычитая две последних формулы, получим (17).
Формулы (17) являются основными в теории тригонометрических функций.
б) Из них следуют «формулы приведения».
Положим
в (17) z1=z,
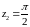 .
Тогда
.
Тогда
 ,
,  .
.
Положим
в (17) z1=z,
 .
Следовательно,
.
Следовательно,
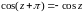 ,
, 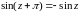 .
.
в) Положим в 1-й из формул (17) z1=z, z2=-z, получим
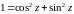 . (18)
. (18)
4
Из (18) не следует, что
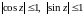 .
.
5
cosz=0
при
 , sinz=0
при
, sinz=0
при
 .
.
cosz=0



Следовательно,
 .
.
Для sinz=0 аналогично.
6 Функции cosz и sinz аналитические в .
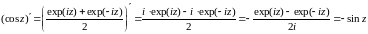 ,
,
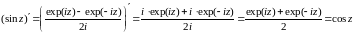 .
.
Определение.
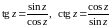 .
.
Свойства tgz и ctgz
1.
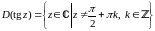 ,
,  .
.
2. tgz=tgx, ctgz=ctgx при .
3.
tg(-z)=-tgz, ctg(-z)=-ctgz
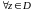 .
.
4. tgz и ctgz – периодические с периодом .
5. tgz и ctgz – непрерывны в своих областях определения.
6. tgz и ctgz – аналитические в своих областях определения,
 ,
,  .
.
7. Нули tgz совпадают с нулями sinz, нули ctgz – с нулями cosz.
8. tgz и ctgz принимают любые значения из , кроме z=i и z=-i.

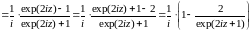 .
.
Следовательно,
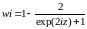
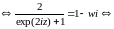


 . (*)
. (*)
Если
w=i,
то (*) примет вид
 – нет решений;
– нет решений;
если
w=-i,
то (*): 0=2 – не имеет смысла. Т. е.
 .
.
Пусть
w=A
( ),
тогда
),
тогда
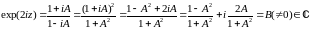 .
.
Следовательно,
существует точка z0:
 .
Т. к.
.
Т. к.
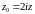 ,
то, следовательно, существует
,
то, следовательно, существует
 .
.
Гиперболические функции
Определение. Гиперболический
косинус  ,
,
гиперболический
синус  . (19)
. (19)
Свойства chz и shz
1
Для
 chz=chx
и shz=shx.
chz=chx
и shz=shx.
2 ch(-z)=chz и sh(-z)=-shz.
3 chz=cos(iz) и shz=-isin(iz) (20)
(или sin(iz)=ishz)
 ,
,

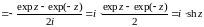 .
.
4
Из (20) следует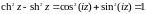 .
.
5 chz и shz аналитические в


6
chz
и shz
- периодические с периодом
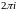 .
.
Вернемся к sinz и cosz.
Определим их действительные, мнимые части и модули.
Покажем,
что
 и
и
 -
неограниченные функции.
-
неограниченные функции.



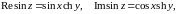

 ,
,
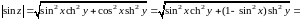
 .
.
Отсюда следует
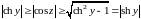 ,
,
 .
.
(эти соотношения можно получить из (15)).
Т.к.
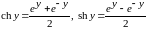 ,
то из последних соотношений заключаем:
,
то из последних соотношений заключаем:
 при
при
 ,
т. е. sinz
и cosz-
неограниченные функции.
,
т. е. sinz
и cosz-
неограниченные функции.
Вопрос 7 Однолистные и многолистные аналитических функций. Логарифмические и степенные функции. Радикал.
Пусть функция w=f(z) - аналитическая в области D. Пусть G - образ области D при отображении w=f(z), т.е. G=f(D).
Определение.
Если
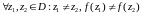 (т.е. в различных точках области D
функция принимает различные значения),
то аналитическая функция w=f(z)
называется однолистной
в
области D.
(т.е. в различных точках области D
функция принимает различные значения),
то аналитическая функция w=f(z)
называется однолистной
в
области D.
Другими словами, однолистная функция w=f(z) взаимно однозначно отображает область D на G.
При
однолистном отображении w=f(z)
прообраз любой точки wG
состоит из единственного элемента:

 :
:
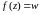 .
.
Поэтому
z
можно рассматривать как функцию от
переменной
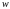 ,
определенную на G.
Она обозначается
,
определенную на G.
Она обозначается
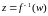 и
называется обратной
функцией.
и
называется обратной
функцией.
Справедливы
тождества: 


и имеет место
Теорема.
Если f(z)-
однолистная и аналитическая на D,
и на
D,
то
-
аналитическая
на G=f(D).
на
D,
то
-
аналитическая
на G=f(D).
Определение.
Если
в области D
существует, по крайней мере, одна пара
точек
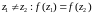 ,
то функцию f(z)
называют многолистной
в области
D.
,
то функцию f(z)
называют многолистной
в области
D.
Если отображение w=f(z) является многолистным на D (например, w=ez, w=sinz, w=cosz, w=zn), то в этом случае некоторым значениям wG соответствует более, чем одна точка zD: f(z)=w.
Следовательно, обратное отображение не является однозначным, оно является многозначной функцией.
Определение. Функция w=f(z) называется многозначной функцией на множестве E, если некоторыми значениям zE соответствует более чем одно значение w.
Теорема. Если аналитическая функция w=f(z) многолистна в области D, то эту область можно разбить на конечное или счетное множество областей, в каждой из которых функция f(z) является однолистной.
К многозначным функциям неприменимы понятия аналитичности и непрерывности. Они могут применяться только к однозначным функциям. Для того, чтобы их использовать, выделяют однозначные ветви многозначных функций.
Определение. Однозначная на области D функция w=f(z) называется ветвью многозначной функции F, если значение f в любой точке zD совпадает с одним из значений F в этой точке.
Е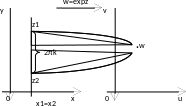 сли
функция w=f(z)
многолистна на D,
то обратная функция
будет
многозначной. Чтобы выделить однозначную
ветвь этой функции поступают, следующим
образом: область D
разбивают на области однолистности
сли
функция w=f(z)
многолистна на D,
то обратная функция
будет
многозначной. Чтобы выделить однозначную
ветвь этой функции поступают, следующим
образом: область D
разбивают на области однолистности
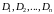 функции w=f(z)
так, что никакие две из областей не имеют
общих внутренних точек и так, чтобы
каждая точка zD
принадлежала одной из этих областей
или границе некоторых из них. В каждой
из этих областей однолистности определяют
функцию, обратную к w=f(z).
Она и является однозначной ветвью
многозначной функции
.
функции w=f(z)
так, что никакие две из областей не имеют
общих внутренних точек и так, чтобы
каждая точка zD
принадлежала одной из этих областей
или границе некоторых из них. В каждой
из этих областей однолистности определяют
функцию, обратную к w=f(z).
Она и является однозначной ветвью
многозначной функции
.
Н айдем
области однолистности функции expz.
Выберем
айдем
области однолистности функции expz.
Выберем
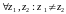

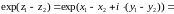
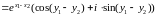
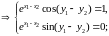




 .
.
Тогда
областью однолистности функции
 будут полоса шириной не больше
будут полоса шириной не больше
 ,
параллельная действительной оси.
,
параллельная действительной оси.
Разобьем
плоскость
 на области однолистности:
на области однолистности:
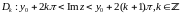 .
.
Если,
например,
 ,
то
,
то
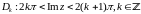 .
.
Логарифмическая функция
Как
было сказано, множество всех корней
уравнения w=ez
(w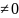 )
представляется формулой
)
представляется формулой
z=ln|w|+iArgw=ln|w|+i(argw+2k) ),
),
 .
.
Значит, функция, обратная к z=ew=eu(cosv+isinv), определена z0, z и задается формулой
w=ln|z|+iArgz.
Эта функция многозначная (бесконечнозначная), называется логарифмической и обозначается Lnz:
w=Lnz=ln|z|+iArgz=ln|z|+i(аrgz+2k).
Назовем значение логарифма ln|z|+iargz главным значением и обозначим через lnz:
lnz=ln|z|+iargz.
Тогда Lnz=lnz+2ki, .
Следовательно,
любое комплексное число z0,
z имеет бесконечное множество логарифмов
(значений логарифмической функции), из
которых любые два отличаются на целое
кратное 2
имеет бесконечное множество логарифмов
(значений логарифмической функции), из
которых любые два отличаются на целое
кратное 2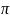 i.
Если
i.
Если
 ,
то Lnz=ln|z|
,
то Lnz=ln|z|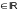 .
Но для этих
существует еще бесконечно много значений
логарифма. Например, Ln2=ln2+2ki,
.
.
Но для этих
существует еще бесконечно много значений
логарифма. Например, Ln2=ln2+2ki,
.
Все логарифмы комплексного числа z имеют одну и ту же действительную часть ln|z|, а мнимые части отличаются на кратное 2. Следовательно, все логарифмы комплексного числа z расположены на комплексной плоскости на одной прямой параллельной оси Оy на расстоянии 2 друг от друга.
Пример.
Ln1=ln1+2k i=2k
i,
.
i=2k
i,
.
Свойства логарифмической функции
1
Ln(z1 z2)=Lnz1+Lnz2.
z2)=Lnz1+Lnz2.
Ln(z1 z2)=ln|z1 z2|+i Arg(z1 z2)=ln|z1|+ln|z2|+i(Argz1+Argz2)=Lnz1+Lnz2.
2
 .
.
 .
.
Замечание.
Эти равенства означают равенство
множеств (в том смысле, что множества
состоят из одних и тех же элементов).
Отсюда следует что, например, Lnz2 2Lnz
2Lnz
Например, Ln(-1)2=Ln1=2ki,
2Ln(-1)=2(+2k)i=i(2+4k),
Ln(-1)2 2Ln(-1): 4i Ln(-1)2, но 4i2Ln(-1).
Степенная функция и радикал
Определение.
Степенной
называется функция вида
 .
.
Если
 ,
то
,
то
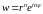 .
Следовательно,
.
Следовательно,
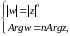

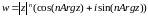
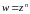 -
многолистная функция.
-
многолистная функция.
 ,
,
 при
при
 .
Следовательно,
.
Следовательно,
 -аналитическая
в
функция.
-аналитическая
в
функция.
Функция
обладает основными свойствами функции
 действительного переменного:
действительного переменного:


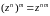 .
.
Найдем
области однолистности функции
.
Выберем
произвольные
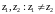 ,
,


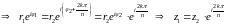
С ледовательно,
областью однолистности функции
будет любой угол с вершиной в начале
координат и раствором
ледовательно,
областью однолистности функции
будет любой угол с вершиной в начале
координат и раствором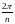 :
:
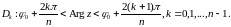
Если
 ,
то
,
то
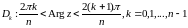 .
.
Радикал
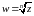 определяется как функция, обратную к
функции
определяется как функция, обратную к
функции
 .
Пусть
.
Пусть
 т.е.
т.е.
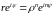 ,
тогда
,
тогда
 .
.
Следовательно,
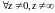 радикал имеет n
различных значений, которые выражаются
формулой
радикал имеет n
различных значений, которые выражаются
формулой
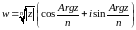
Следовательно,
функция
является
многозначной (n
– значной). Эти n
значений располагаются в вершинах
правильного n
– угольника, вписанного в окружность
 .
При
.
При
 и
и
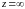 получаем по одному значению функции
получаем по одному значению функции
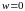 и
и
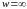 .
.
Чтобы
выделить однозначную ветвь, достаточно
указать, в какой области однолистности
изменяется w.
Мы установили выше, что областью
однолистности функции
 является
угол с вершиной в начале координат и
раствором
:
является
угол с вершиной в начале координат и
раствором
:

Любой
луч плоскости (
)
 при
отображении
переходит
в луч плоскости (z):
при
отображении
переходит
в луч плоскости (z):
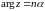 .
Если луч
пробегает
область
.
Если луч
пробегает
область
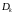 против хода часовой стрелки, то луч
пробежит всю плоскость (z)
от
против хода часовой стрелки, то луч
пробежит всю плоскость (z)
от
 до
до
 .
Следовательно, любая из областей
однолистности
перейдет в одну и ту же область
.
Следовательно, любая из областей
однолистности
перейдет в одну и ту же область
 плоскости (z):
угол раствора 2π, границей которой служит
луч
плоскости (z):
угол раствора 2π, границей которой служит
луч
 .
.
Т аким
образом, в области
получаем n
однозначных ветвей функции
Каждая из них определяется условием,
что ее значения
принадлежат области
.
аким
образом, в области
получаем n
однозначных ветвей функции
Каждая из них определяется условием,
что ее значения
принадлежат области
.
Будем
обозначать эти ветви
 .
.
Вопрос №8. Достаточное условие существования интеграла
Определение.
Если
существует конечный предел интегральной
суммы (1) при
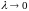 (или
при
(или
при
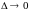 ),
не зависящий ни от способа разбиения T
кривой L,
ни от выбора точек
),
не зависящий ни от способа разбиения T
кривой L,
ни от выбора точек
 ,
то этот предел называется интегралом
от функции f(z)
по кривой L
и обозначается
,
то этот предел называется интегралом
от функции f(z)
по кривой L
и обозначается
 .
.
Таким
образом,
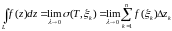 .
.
В этом случае функция f(z) называется интегрируемой по кривой L.
Теорема
1 (достаточное
условие существования интеграла от
функции комплексного переменного).
Пусть L
– простая гладкая кривая на
,
f(z)=u(x;y)+iv(x;y)
непрерывна на L.
Тогда существует
 ,
причем справедливо равенство:
,
причем справедливо равенство:
 . (2)
. (2)
Доказательство.
Выберем
произвольно разбиение T
кривой L
на дуги
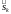 ,
на каждой
выберем произвольно точку
.
Составим интегральную сумму
,
на каждой
выберем произвольно точку
.
Составим интегральную сумму
 .
Выделим в
.
Выделим в
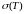 действительную и мнимые части:
действительную и мнимые части:
z=x+iy,
f(z)=u(x;y)+iv(x;y),
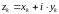 ,
,
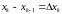 ,
,
 ,
,
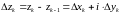 ,
,
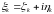 .
Тогда
.
Тогда

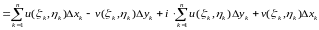 . (3)
. (3)
В
правой части (3) стоят интегральные суммы
для криволинейных интегралов II типа
двух действительных функций u(x;y)
и v(x;y).
Если
 и
и
 ,
то и
,
то и
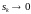
 (или
).
(или
).
Т.к. L – гладкая кривая, а функции u(x;y) и v(x;y) непрерывны на L, то
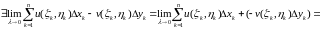

и 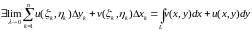 .
.
Тогда существует предел при левой части (3), т.е. существует .
Переходя в (3) к пределу при , получим (2).
Вычисление интеграла от функции комплексного переменного
Пусть вначале f(t)=u(t)+iv(t) –комплексно-значная функция действительной переменной. Тогда интеграл от f(t) по отрезку [a;b] определяется следующим образом:
 .
.
Рассмотрим теперь интеграл от функции комплексного переменного по кривой L.
Теорема 2.Пусть L – простая гладкая кривая, заданная параметрически:
L:
z(t)=x(t)+iy(t),
t,
функция f(z)
непрерывна на L.
Тогда справедливо равенство:
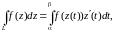 (где
(где
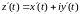 ).
).
Доказательство.
Т.к. выполнены условия теоремы 1, то имеет место равенство (2) . Каждый криволинейный интеграл II типа можно заменить по формуле, сводящей его вычисление к вычислению обычного определенного интеграла:
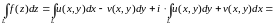
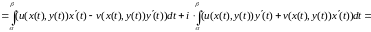

= .
.
Вопрос №9. Необходимое и достаточное условие независимости интеграла. Интегральная теорема Коши.
Рассмотрим
 .
Он зависит от функции f(z)
и от вида кривой L.
Возникает вопрос: каким условиям должна
удовлетворять функция f(z),
чтобы интеграл не зависел от пути
интегрирования L,
а определялся начальной и конечной
точками кривой.
.
Он зависит от функции f(z)
и от вида кривой L.
Возникает вопрос: каким условиям должна
удовлетворять функция f(z),
чтобы интеграл не зависел от пути
интегрирования L,
а определялся начальной и конечной
точками кривой.
Как и в случае криволинейного интеграла II рода независимость интеграла от пути интегрирования равносильна равенству нулю этого интеграла по любому замкнутому контуру.
Теорема.
не
зависит от пути интегрирования на
области D
тогда и только тогда, когда
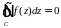 по любому кусочно-гладкому контуру
по любому кусочно-гладкому контуру
 .
.
Доказательство.
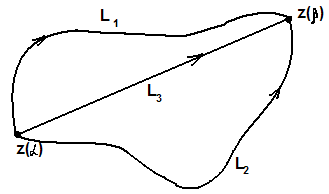
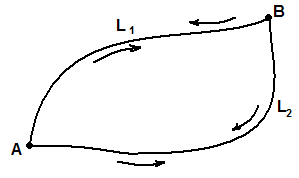 (
( )
Пусть
)
Пусть
 ,
где
,
где
 и
и
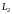 -кривые,
лежащие в D
и соединяющие точки A
и B.
Тогда
-кривые,
лежащие в D
и соединяющие точки A
и B.
Тогда
 ,
где
,
где
 .
.
( )
Пусть
,
где C
- кусочно-гладкий замкнутый контур,
.
Разобьем C
точками A
и B
на кривые
и
так, что
.
Тогда
)
Пусть
,
где C
- кусочно-гладкий замкнутый контур,
.
Разобьем C
точками A
и B
на кривые
и
так, что
.
Тогда


Для доказательства интегральной теоремы Коши нам понадобится следующая
Л емма.
Пусть
f(z)-
непрерывная в области G
функция, L
- произвольная кусочно - гладкая линия,
LG.
Тогда >0
существует ломаная P,
вписанная в L,
PG,
такая что
емма.
Пусть
f(z)-
непрерывная в области G
функция, L
- произвольная кусочно - гладкая линия,
LG.
Тогда >0
существует ломаная P,
вписанная в L,
PG,
такая что
 .
.
Доказательство.
 Разобьём
L
на частичные дуги
Разобьём
L
на частичные дуги
 ,
,
 ,…,
,…,
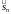 sk
– длина
).
Впишем в L
ломаную P,
звенья которой стягивают дуги
.
Точки z0,
z1,…,zn
– вершины ломаной P.
Звенья ломаной (и их длины) обозначим
через lk
,
k=
sk
– длина
).
Впишем в L
ломаную P,
звенья которой стягивают дуги
.
Точки z0,
z1,…,zn
– вершины ломаной P.
Звенья ломаной (и их длины) обозначим
через lk
,
k=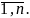
Рассмотрим сумму
S=f(z1)z1+f(z2)z2+…+f(zn)zn . (4)
S
является интегральной суммой для
интеграла
,
в которой в качестве точек k
взяты точки zk.
Так
как f(z)
– непрерывна в G,
а L
–
кусочно – гладкая линия, то
 (
( ),
т.е. >0
1>0:
T:
<1
),
т.е. >0
1>0:
T:
<1
 . (5),
. (5),
Оценим
 .
Так как
.
Так как
 ,
то (4) примет вид:
,
то (4) примет вид:
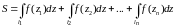 .
(6)
.
(6)
С
другой стороны,
 . (7)
. (7)
Вычтем (6) из (7):
 .
.
Так
как функция f(z)
непрерывна
в G,
то она равномерно непрерывна на любом
ограниченном замкнутом множестве точек
из G.
Следовательно, она непрерывна на ломаной
P.
По определению равномерной непрерывности:
для выбранного числа >0
2>0:
z,
zP:
|z-z|<2
выполнено
 .
Пусть <2.
Так как k
на звене lk
|z-zk|<
lk<<2,
то
.
Пусть <2.
Так как k
на звене lk
|z-zk|<
lk<<2,
то
 .
Тогда
.
Тогда
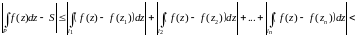
 .
(8)
.
(8)
Выберем =min{1;2}. Из (5) и (8) получим: >0 >0: T: < выполнено
 .
.
Итак,
в линию L
всегда можно вписать ломаную P
так, что разность значений
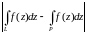 будет
меньше любого наперёд заданного числа.
будет
меньше любого наперёд заданного числа.

I. Случай односвязной области
Теорема
(Коши для односвяз.). Если
f(z)
аналитическая в односвязной области G
функция, то ,
где L-
любой замкнутый контур, лежащий в G.
,
где L-
любой замкнутый контур, лежащий в G.
Доказательство.
 Согласно
лемме в линию L
можно вписать ломаную P
так, что
Согласно
лемме в линию L
можно вписать ломаную P
так, что
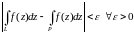 .
.
Следовательно,
если мы докажем, что
 ,
то отсюда будет следовать что
,
то отсюда будет следовать что
 и, значит,
.
и, значит,
.
Следовательно, теорему достаточно доказать для случая, когда контуром интегрирования является ломаная P.
Далее:
данный многоугольник с периметром P
можно разбить на треугольники. Тогда
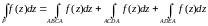 ,
так как по AC,
DA
интегрирование совершается два раза в
противоположных направлениях.
Следовательно, если допустить, что
теорема Коши доказана для случая, когда
контуром интегрирования является любой
треугольник, то из последнего равенства
будет следовать, что
.
,
так как по AC,
DA
интегрирование совершается два раза в
противоположных направлениях.
Следовательно, если допустить, что
теорема Коши доказана для случая, когда
контуром интегрирования является любой
треугольник, то из последнего равенства
будет следовать, что
.
И так,
докажем, что если f(z)
– аналитическая в области G
функция, то
так,
докажем, что если f(z)
– аналитическая в области G
функция, то ,
где -
периметр любого треугольника, лежащего
в G.
,
где -
периметр любого треугольника, лежащего
в G.
Положим
 и докажем, что M=0.
и докажем, что M=0.
Р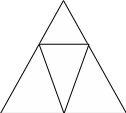 азделим
стороны треугольника пополам и соединим
точки деления. Треугольник, таким
образом, разобьётся на четыре равных
треугольника 1,
2,
3,
4.
азделим
стороны треугольника пополам и соединим
точки деления. Треугольник, таким
образом, разобьётся на четыре равных
треугольника 1,
2,
3,
4.
 .
.
Так как , то существует периметр k:
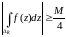 .
.
С
этим треугольником k=(1)
поступим так же, как и с ,
разбив на четыре разных треугольника.
Следовательно, существует треугольник
с периметром (2)(1):
 .
.
Этот процесс продолжим неограниченно, получим последовательность треугольников с периметрами =(0), (1), (2),…, (n),…, из которых каждый содержит следующий и таких, что:
 (n=0,1,…). (9)
(n=0,1,…). (9)
Обозначим
периметр
через U.
Тогда периметр
 .
.
Оценим
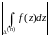 .
Имеем {(n)}
– последовательность вложенных
треугольников. Их периметры стремятся
к 0 при n.
Следовательно, существует точка z0,
принадлежащая всем треугольникам
последовательности {(n)}.
Так как z0G,
а f(z)-аналитическая
в G,
то
.
Имеем {(n)}
– последовательность вложенных
треугольников. Их периметры стремятся
к 0 при n.
Следовательно, существует точка z0,
принадлежащая всем треугольникам
последовательности {(n)}.
Так как z0G,
а f(z)-аналитическая
в G,
то
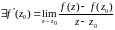 .
Следовательно, >0
()>0:
z:
|z-z0|<
выполнено
.
Следовательно, >0
()>0:
z:
|z-z0|<
выполнено
 ,
отсюда
,
отсюда
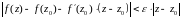 . (10)
. (10)
Начиная
с достаточно большого номера n0,
треугольник (n)
будет находиться в круге
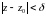 и, следовательно, для оценки
можно использовать (10). Заметим, что
и, следовательно, для оценки
можно использовать (10). Заметим, что

 ,
,
так
как
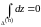 и
и
 (см.
пример о
(см.
пример о
 ).
).
Тогда
 .
.
Так
как z0(n),
то
 (расстояние между z
и z0
меньше периметра).
(расстояние между z
и z0
меньше периметра).
Следовательно,
 . (11)
. (11)
Из
(9) и (11) следует
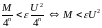 .
Так как -
произвольное сколь угодно малое число,
то переходя к пределу при
.
Так как -
произвольное сколь угодно малое число,
то переходя к пределу при  0,
получим M=0.
Следовательно,
.
0,
получим M=0.
Следовательно,
.

II. Случай многосвязной области
Пусть
D-
многосвязная область, граница которой
L
состоит из внешнего контура L0
и внутренних L1,
L2,…
Ln,
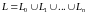 ,
(D-
(n+1)-связная
область).
,
(D-
(n+1)-связная
область).
Определение. Положительным обходом границы L многосвязной области D называется такое направление обхода каждого контура, при котором область D остаётся всё время слева.
Теорема
(Коши для многосвяз.). Пусть
f(z)
– аналитическая в области G,
D
– многосвязная область, которая вместе
со своей границей L
целиком лежит в G.
Т огда
,
где интеграл берётся в положительном
направлении.
огда
,
где интеграл берётся в положительном
направлении.
Доказательство.
Рассмотрим
случай n=2:
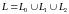 .
Соединим контуры L1
и L2
c
внешним контуром L0
линиями l1,
l2
(l1
и l2
выберем
так, чтобы они не пересекались). Т.о., мы
получим односвязную область D*,
которая ограничена кривыми
L0,
L1,
L2,
l1,
l2,
причём
l1,
l2
проходятся
дважды в противоположных направлениях.
.
Соединим контуры L1
и L2
c
внешним контуром L0
линиями l1,
l2
(l1
и l2
выберем
так, чтобы они не пересекались). Т.о., мы
получим односвязную область D*,
которая ограничена кривыми
L0,
L1,
L2,
l1,
l2,
причём
l1,
l2
проходятся
дважды в противоположных направлениях.
 .
– граница D*.
По предыдущей теореме
.
– граница D*.
По предыдущей теореме
 Пользуясь свойством аддитивности
интеграла получим:
Пользуясь свойством аддитивности
интеграла получим:
 Следствие.
Если l1
и l2
кусочно – гладкие замкнутые кривые
ограничивающие кольцеобразную область
в области G,
и функция f(z)
– аналитическая в G,
то
Следствие.
Если l1
и l2
кусочно – гладкие замкнутые кривые
ограничивающие кольцеобразную область
в области G,
и функция f(z)
– аналитическая в G,
то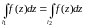 .
.
Вопрос №10. Первообразная. Формула ньютона-Лейбница.
Если
f(z)
аналитическая в односвязной области D
функция, то, как было установлено,
значение
,
взятого по любой кусочно – гладкой
кривой LD,
не зависит от вида кривой, а определяется
лишь начальной и конечной точками
кривой. Поэтому для интеграла вдоль
произвольной кусочно – гладкой кривой
L,
соединяющей точки z0
и z,
используют обозначение ,
где z0
и z
называются соответственно, нижним и
верхним пределами интегрирования.
,
где z0
и z
называются соответственно, нижним и
верхним пределами интегрирования.
Зафиксируем
z0,
тогда
зависит только от точки z,
т.е. является однозначной функцией,
определённой на D,
т.е.
 .
.
Теорема
1.
Пусть f(z)-функция,
непрерывная в области D,
для которой интеграл
вдоль любой кусочно – гладкой кривой
LD
не
зависит от вида кривой, а определяется
только начальной и конечной точками
кривой. Тогда
является аналитической на D
функцией и F'(z)=f(z)
 .
.
Доказательство.
Пусть
L D-кусочно-гладкая
кривая, соединяющая точки z0
и z.
Выберем ∆z≠0
так, чтобы z+∆z
D-кусочно-гладкая
кривая, соединяющая точки z0
и z.
Выберем ∆z≠0
так, чтобы z+∆z D.
D.
 .
.
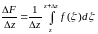
 . (1)
. (1)
Т.к.
 ,
то
,
то
 . (2)
. (2)
Интегралы (1) и (2) не зависят от пути интегрирования, поэтому в качестве пути от z до z+∆z можно взять прямолинейный отрезок, соединяющий эти точки. Из (1) и (2) следует:
 . (3)
. (3)
Зафиксируем >0. Так как f(z) непрерывна на D, то для любой точки z D выполнено

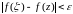 . (4)
. (4)
В
равенстве (3)
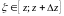 .
Следовательно,
.
Следовательно,

 .
Поэтому если
.
Поэтому если
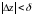 ,
то
,
то
 ,
значит, выполнено
(4).
,
значит, выполнено
(4).
Тогда из (3) следует

 .
.
Таким
образом,
 .
.
По
определению это означает, что
 ,
,
то есть F'(z)=f(z) .
Замечание 1. Теорему 1 можно было сформулировать следующим образом:
если
f(z)
аналитическая в области D
функция, то
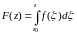 - аналитическая функция и F'(z)=f(z),
где интеграл берётся по любой
кусочно-гладкой кривой, соединяющей
точки z0
и z.
- аналитическая функция и F'(z)=f(z),
где интеграл берётся по любой
кусочно-гладкой кривой, соединяющей
точки z0
и z.
Действительно,
если f(z)
– аналитическая функция, то
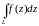 не
зависит от пути интегрирования.
не
зависит от пути интегрирования.
Определение. Функция F(z) называется первообразной для функции f(z) на области G, если F'(z)=f(z) .
Из
определения следует, что если F(z)
первообразная для f(z)
на D,
то и функция F(z)+C
является первообразной для f(z)
на D
(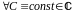 ).
).
Следовательно, если выполнены условия теоремы 1, то функция f(z) имеет первообразную.
Теорема 2. Если f(z)-аналитическая на односвязной области D, и F(z), (z)-две первообразные для f(z) на D, то справедливо F(z)-Φ(z)=С=const.
Доказательство.
Пусть F(z) и Φ(z) - две первообразные функции f(z) на D. Рассмотрим функцию w(z)=F(z)-Φ(z) , w(z)=u(x,y)+iv(x,y).
Тогда w(z)=F'(z)-Φ'(z)=f(z)-f(z)=0 .
Так
как
 ,
то
,
то
 и
и
 .
.
Так
как w(z)
- аналитическая
функция, то
 и
и
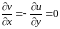 .
.
Итак,
,

u=aconst,
u=aconst,
,

v=bconst.
v=bconst.
Тогда w(z)=a+ibconst.
Значит, F(z)-Φ(z)=С.
Следствие 1. Если f(z)-аналитическая на односвязной области D, то любая её первообразная имеет вид
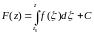 ,
где
,
где
 . (5)
. (5)
Следствие 2. Положим в (5) z=z0, тогда C=F(z0).Заменяя в (5) C на F(z0) получим:
 -
формула Ньютона-Лейбница.
-
формула Ньютона-Лейбница.
Таким образом, интеграл от аналитической функции комплексной переменной вычисляется с помощью тех же методов и формул, что и в случае функции действительной переменной.
Вопрос №11. Интегральная формула Коши и ее следствия
Интегральная формула Коши
Теорема. Пусть функция f(z) аналитическая в односвязной области D, L-произвольный замкнутый кусочно-гладкий контур, лежащий в D. Тогда для любой точки z0, лежащей внутри контура L, справедлива формула:
 , (1)
, (1)
где L обходится в положительном направлении.
(1) - интегральная формула Коши. Она выражает значения аналитической функции внутри контура через её значения на контуре.
Доказательство.

 Пусть
z0-
произвольная точка, лежащая внутри
контура L.
Рассмотрим окружность γr:
|z-z0|=r
, где r
выберем так, чтобы γr
лежала внутри L.
В двусвязной области, ограниченной
контурами L
и
γr,
функция
Пусть
z0-
произвольная точка, лежащая внутри
контура L.
Рассмотрим окружность γr:
|z-z0|=r
, где r
выберем так, чтобы γr
лежала внутри L.
В двусвязной области, ограниченной
контурами L
и
γr,
функция
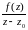 является
аналитической, следовательно, она
аналитическая и на области
является
аналитической, следовательно, она
аналитическая и на области
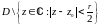 .
Тогда по следствию из теоремы Коши:
.
Тогда по следствию из теоремы Коши:
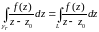 . (2)
. (2)
Из
(2) следует, что значение
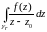 не
зависит от радиуса окружности γr.
не
зависит от радиуса окружности γr.
Из (2) следует, что для доказательства (1) достаточно показать, что
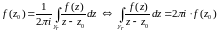 . (3)
. (3)
Так
как
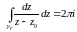 ,
то
,
то
 или
или
 . (4)
. (4)
Из (3) и (4) следует, что для доказательства (1) надо доказать, что
 . (5)
. (5)
Заметим, что интеграл в (5) не зависит от r .
Возьмем
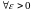 .
Так как f(z)
аналитическая на D,
то f(z)
непрерывна в точке z0D.
Тогда
.
Так как f(z)
аналитическая на D,
то f(z)
непрерывна в точке z0D.
Тогда
 выполнено
выполнено
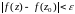 .
.
Если
γr
такая, что r<δ,
то
 выполнено
|z-z0|=r<δ
|f(z)-f(z0)|<ε.
выполнено
|z-z0|=r<δ
|f(z)-f(z0)|<ε.
 . (6)
. (6)
Так как ε>0 – произвольное сколь угодно малое число, а значение интеграла не зависит от r, то (6) может быть выполнено только если , то есть выполнено (5), а значит, выполнено (1).
Следствие . Если две аналитические в односвязной области D функции f(z) и g(z) совпадают на замкнутом контуре LD, то они совпадают и внутри контура L.
Замечание.
Если
точка z0
лежит вне контура L,
то
 .
.
Действительно, в этом случае является аналитической не только на L, но и внутри L, следовательно, применима интегральная формула Коши, согласно которой этот интеграл равен 0.
Итак,