
- •16. Комплексное представление сопротивлений и проводимостей.
- •17. Активная, реактивная и полная мощности.
- •18. Резонанс токов в параллельной цепи r, l и c.
- •19. Резонанс напряжений в последовательной цепи r, l и c.
- •2 0. Трехфазная цепь. Соединение “звезда”.
- •21. Трехфазная цепь. Соединение “треугольник”.
- •22. Мощность трехфазной цепи.
- •23. Системы электроснабжения.
- •24. Общие сведения об источниках электрической энергии.
- •25. Магнитные величины и ферромагнетики.
- •26. Магнитные цепи и их расчет.
- •27. Электромагнитные устройства.
- •28. Трансформаторы: назначение, устройство, характеристики. Виды трансформаторов.
- •29. Схема замещения трансформатора, расчет. Режим работы.
- •30. Электрические машины: электропривод, классификация, общие вопросы.
19. Резонанс напряжений в последовательной цепи r, l и c.
Р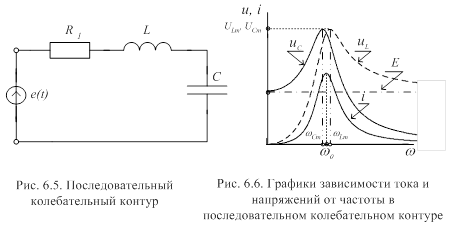 езонанс
напряжений возникает в цепи с
последовательным соединением элементов
(рис. 6.5). Известно, что комплексное
сопротивление такой цепи определяется
выражением
езонанс
напряжений возникает в цепи с
последовательным соединением элементов
(рис. 6.5). Известно, что комплексное
сопротивление такой цепи определяется
выражением
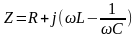 .
По определению резонанс в цепи рис.6.5
наступает, когда выполнится условие
.
По определению резонанс в цепи рис.6.5
наступает, когда выполнится условие
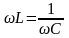 .
Отсюда видно, что резонанс в цепи
возникает на частоте
.
Отсюда видно, что резонанс в цепи
возникает на частоте
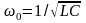 .
Очевидно также, что
.
Очевидно также, что
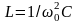 ,
,
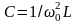 .
Определим
ток и напряжение всей цепи, а также
падение напряжения на ее отдельных
элементах в режиме резонанса. Так как
сопротивление всей цепи в режиме
резонанса минимально и равно R,
то ток в ней максимален и равен
.
Определим
ток и напряжение всей цепи, а также
падение напряжения на ее отдельных
элементах в режиме резонанса. Так как
сопротивление всей цепи в режиме
резонанса минимально и равно R,
то ток в ней максимален и равен
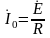 .
Падение напряжения на отдельных
элементах легко найти по закону Ома.
Так, падение напряжения на резисторе R
равно
.
Падение напряжения на отдельных
элементах легко найти по закону Ома.
Так, падение напряжения на резисторе R
равно
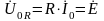 .
Тривиальный математически результат
интересен по физической сути – при
резонансе все напряжение источника
выделяется на R
элементе цепи. Падение напряжения на
индуктивности определяется выражением:
.
Тривиальный математически результат
интересен по физической сути – при
резонансе все напряжение источника
выделяется на R
элементе цепи. Падение напряжения на
индуктивности определяется выражением:
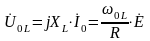 .
Величина
.
Величина
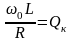 называется добротностью и может принимать
значение десятков и сотен единиц.
Значит, падение напряжения на индуктивности
может в десятки и сотни раз превышать
Э.Д.С. источника. Падение напряжения на
емкости равно
называется добротностью и может принимать
значение десятков и сотен единиц.
Значит, падение напряжения на индуктивности
может в десятки и сотни раз превышать
Э.Д.С. источника. Падение напряжения на
емкости равно
 .
Так как
.
Так как
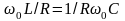 ,
то падение напряжения на емкости равно
по величине падению напряжения на
индуктивности, но они противоположны
по знаку. Отношение
напряжения на индуктивности или на
емкости в режиме резонанса к току в этом
режиме называют характеристическим
сопротивлением – ρ,
причем
,
то падение напряжения на емкости равно
по величине падению напряжения на
индуктивности, но они противоположны
по знаку. Отношение
напряжения на индуктивности или на
емкости в режиме резонанса к току в этом
режиме называют характеристическим
сопротивлением – ρ,
причем
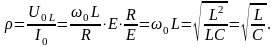 В силу того, что
В силу того, что
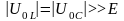 ,
рассматриваемый режим назван резонансом
напряжений. Противоположность фаз
напряжений
,
рассматриваемый режим назван резонансом
напряжений. Противоположность фаз
напряжений

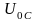 и
и
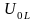 указывает на то, что в цепи происходит
такой же колебательный процесс с частотой
ω0,
как и в параллельном колебательном
контуре. Здесь также энергия источника
затрачивается только на преодоление
сопротивления резистора R.
Поэтому цепь называется последовательным
колебательным контуром. Завершим анализ
резонанса напряжений построением
частотной зависимости тока цепи (рис.6.5)
и падений напряжений на элементах L
и С
(рис.6.6). На рисунке штрихпунктирной
линией отмечен график ЭДС. На частоте
ω=0
сопротивление идеальной индуктивности
отсутствует. Поэтому падение напряжения
uL
также равно нулю. С увеличением частоты
сопротивление индуктивности, а значит,
и падение напряжения на ней, увеличиваются.
Когда частота устремляется в бесконечность,
сопротивление ХL
также устремляется в бесконечность.
При этом падение напряжения uL
стремится
к Е.
Между крайними точками графика uL=ƒ(ω)
существует
экстремум напряжения
указывает на то, что в цепи происходит
такой же колебательный процесс с частотой
ω0,
как и в параллельном колебательном
контуре. Здесь также энергия источника
затрачивается только на преодоление
сопротивления резистора R.
Поэтому цепь называется последовательным
колебательным контуром. Завершим анализ
резонанса напряжений построением
частотной зависимости тока цепи (рис.6.5)
и падений напряжений на элементах L
и С
(рис.6.6). На рисунке штрихпунктирной
линией отмечен график ЭДС. На частоте
ω=0
сопротивление идеальной индуктивности
отсутствует. Поэтому падение напряжения
uL
также равно нулю. С увеличением частоты
сопротивление индуктивности, а значит,
и падение напряжения на ней, увеличиваются.
Когда частота устремляется в бесконечность,
сопротивление ХL
также устремляется в бесконечность.
При этом падение напряжения uL
стремится
к Е.
Между крайними точками графика uL=ƒ(ω)
существует
экстремум напряжения
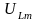 ,
который находится по формуле
,
который находится по формуле
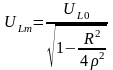 .
.
Частота,
на которой достигается этот максимум,
определяется формулой:
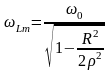 .
.
Сопротивление
емкости на частоте ω=0
равно
бесконечности. Значит, напряжение на
ее обкладках равно Е.
С увеличением частоты сопротивление
ХС
уменьшается. Когда частота устремляется
в бесконечность, сопротивление XC
устремляется к нулю. Между крайними
точками также существует экстремум,
причем
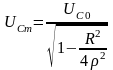 .
Частота, на которой достигается этот
максимум, определяется выражением
.
Частота, на которой достигается этот
максимум, определяется выражением
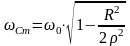 .
Так как подкоренное выражение в всегда
меньше единицы, то очевидно, что
.
Так как подкоренное выражение в всегда
меньше единицы, то очевидно, что
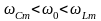 .
Кроме того
.
Кроме того
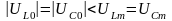 .
В силу этих особенностей достоверным
признаком наступления резонанса в цепи
является максимум тока, значение которого
изменяется с изменением частоты по
резонансной кривой.
.
В силу этих особенностей достоверным
признаком наступления резонанса в цепи
является максимум тока, значение которого
изменяется с изменением частоты по
резонансной кривой.
