25. Поток вектора напряженности электростатического поля. Теорема Гаусса. Интегральная и дифференциальная формы.

Поток вектора напряженности электростатического поля.

Электростатическое поле наглядно можно изобразить с помощью силовых линий (линий напряженности). Силовыми линиями называют кривые, касательные к которым в каждой точке совпадают с вектором напряженности Е.

Силовые линии являются условным понятием и реально не существуют. Силовые линии одиночного отрицательного и одиночного положительного зарядов 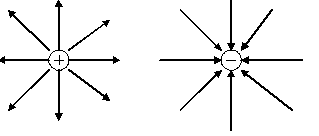Рис.5

Если густота и направление силовых линий по всему объему поля сохраняются неизменными, такое электростатическое поле считается однородным. Например, заряд, распределенный равномерно по бесконечной плоскости, создает однородное электрическое поле, силовые линии которого изображаются равноотстоящими друг от друга параллельными прямыми линиями. Для того, чтобы силовые линии характеризовали не только направление поля, но и значение его напряженности, число линий должно быть численно равно напряженности поля Е.

Число силовых линий dФ_Е, пронизывающих площадку dS, перпендикулярную к ним, определяет поток вектора напряженности электростатического поля:

где E_n= Еcos α - проекция вектора Е на направление нормали n к площадке dS.

Соответственно поток вектора Е сквозь произвольную замкнутую поверхность S

Теорема Гаусса

Зная дивергенцию вектора а в каждой точке пространства, можно вычислить поток этого вектора через любую замкнутую поверхность конечных размеров.

Сделаем это сначала для потока вектора v (потока жидкости). Произведение divv на dVдает мощность источников жидкости, заключенных в объеме dV. Сумма таких произведений, т. е. , дает сум­марную алгебраическую мощность источников, заключенных в объе­ме V, по которому осуществляется интегрирование. Вследствие несжимаемости жидкости суммарная мощность источников должна равняться потоку жидкости, вытекающему наружу через поверх­ность S, ограничивающую объем V. Таким образом, мы приходим к соотношению

Аналогичное соотношение выполняется для векторного поля любой природы:

Это соотношение носит название теоремыОстроград­ского — Гаусса. Интеграл в левой части соотношения вычи­сляется по произвольной замкнутой поверхности S, интеграл в правой части — по объему V, ограниченному этой поверхностью.

Теорема Гаусса: Эта теорема гласит, что поток вектора напряженности электрического поля через замкнутую поверхность равен алгебраической сумме заключенных внутри этой поверхности зарядов, деленной на .

41. Закон Ома для однородного проводника. Закон Ома в дифференциальной форме.

Немецкий физик Г. Ом (1787—1854) экспериментально установил, что сила тока I, текущего по однородному металлическому проводнику (т. е. проводнику, в котором не действуют сторонние силы), пропорциональна напряжению Uна концах проводника:

(1) гдеR— электрическое сопротивление проводника. Уравнение (1) выражает закон Ома для участкацепи (не содержащего источника тока): сила тока в проводнике прямо пропорциональна приложенному напряжению и обратно пропорциональна сопротивлению проводника. Формула (1) позволяет установить единицу сопротивления — ом (Ом) 1 Ом — сопротивление такого проводника, в котором при напряжении 1 В течет постоянный ток 1 А. Величина G=1/R называется электрической проводимостью проводника. Единица проводимости — сименс(См): 1 См — проводимость участка электрической цепи сопротивлением 1 Ом. Сопротивление проводников зависит от его размеров и формы, а также от материала, из которого проводник изготовлен. Для однородного линейного проводника противление Rпрямо пропорционально его длине lи обратно пропорционально площади его поперечного сечения S: (2)где — коэффициент пропорциональности, характеризующий материал проводниканазываемый удельным электрическим сопротивлением. Единица удельного электрического сопротивления — Ом-метр (Ом·м).

Закон Ома можно представить в дифференциальной форме.

Подставив выражение для сопротивления (2) в закон Ома (1), получим (3)где

величина, обратная удельному сопротивлению, называется удельной электрической проводимостью вещества проводника. Ее единицасименс на метр (См/м). Учитывая, что — напряженность электрического в проводнике, I/S=j— плотность тока, формулу (3) можно записать в виде Так как в изотропном проводнике носители тока в каждой точке движутся в направлении вектора Е, то направления j и Е совпадают. Поэтому формулу можно записать в виде . Это выражение — закон Ома в дифференциальнойформе, связывающий плотность тока в любой точке внутри проводника с напряженностью электрического поля в этой же точке. Это соотношение справедливо и для переменных полей.