8. Работа. Кинетическая энергия частицы.

Кинети́ческая эне́ргия — энергия механической системы, зависящая от скоростей движения её точек. Часто выделяют кинетическую энергию поступательного и вращательного движения.

Более строго, кинетическая энергия есть разность между полной энергией системы и её энергией покоя; таким образом, кинетическая энергия — часть полной энергии, обусловленная движением.

и/или

Механическая энергия бывает двух видов: кинетическая и потенциальная. Кинетическая энергия (или энергия движения) определяется массами и скоростями рассматриваемых тел. Потенциальная энергия (или энергия положения) зависит от взаимного расположения (от конфигурации) взаимодействующих друг с другом тел.

Работа определяется как скалярное произведение векторов силы и перемещения. Скалярным произведением двух векторов называется скаляр равный произведению модулей этих векторов и косинус угла между ними.

Понятия энергии и работы тесно связаны друг с другом.

Кинетическая энергия частицы

доп.

работа результирующей всех сил, действующих на частицу, идет на приращение кинетической энергии частицы.

№10 Момент импульса тела, вращающегося вокруг неподвижной оси.

Момент импульса материальной точки относительно точки O определяется векторным произведением , где   — радиус-вектор, проведенный из точки O,   — импульс материальной точки. Момент импульса материальной точки относительно неподвижной оси    равен проекции на эту ось вектора момента импульса, определенного относительно произвольной точки O данной оси. Значение момента импульса    не зависит от положения точки O на оси z.

Момент импульса твердого тела относительно оси есть сумма моментов импульса отдельных частиц, из которых состоит тело относительно оси. Учитывая, что  , получим .

Если сумма моментов сил, действующих на тело, вращающееся вокруг неподвижной оси, равна нулю, то момент импульса сохраняется (закон сохранения момента импульса):  .

Производная момента импульса твердого тела по времени равна сумме моментов всех сил, действующих на тело: .

№11 Момент импульса системы. Закон сохранения момента импульса.

Монет импульса твердого тела относительно оси есть сумма моментов импульса отдельных частиц:    Используя формулу v_i = ωr_i, получим    т. е.   2)  Таким образом, момент импульса твердого тела относительно оси равен моменту инерции тела относительно той же оси, умноженному на угловую скорость. Продифференцируем уравнение (2) по времени:    т. е.    Эта формула - еще одна форма уравнения динамики вращательного движения твердого тела относительно неподвижной оси: производная момента импульса твердого тела относительно оси равна моменту сил относительно той же оси.  Можно показать, что имеет место векторное равенство  (3)  В замкнутой системе момент внешних сил   и   откуда   (4)  Выражение (4) представляет собой закон сохранения момента импульса: момент импульса замкнутой системы сохраняется, т. е. не изменяется с течением времени.  Закон сохранения момента импульса также как и закон сохранения энергии является фундаментальным законом природы. Он связан со свойством симметрии пространства - его изотропностью, т. е. с инвариантностью физических законов относительно выбора направления осей координат системы отсчета (относительно поворота замкнутой системы в пространстве на любой угол). 

№12 Момент импульса и момент силы относительно точки и оси. Уравнение моментов.

Моментом импульса (количества движения) материальной точки А относительно неподвижной точки О называется физическая величина, определяемая векторным произведением:    где r - радиус-вектор, проведенный из точки О в точку A, p=mv - импульс материальной точки (рис. 1); L - псевдовектор, направление которого совпадает с направлением поступательного движения правого винта при его вращении от r к р.

Рис.1

Модуль вектора момента импульса    где α - угол между векторами r и р, l - плечо вектора р относительно точки О. 

Моментом импульса относительно неподвижной оси z называется скалярная величина L_z, равная проекции на эту ось вектора момента импульса, определенного относительно произвольной точки О данной оси. Момент импульса L_z не зависит от положения точки О на оси z.  При вращении абсолютно твердого тела вокруг неподвижной оси z каждая точка тела движется по окружности постоянного радиуса r_iсо скоростью v_i . Скорость v_i и импульс m_iv_i перпендикулярны этому радиусу, т. е. радиус является плечом вектора m_iv_i . Значит, мы можем записать, что момент импульса отдельной частицы равен  (1)  и направлен по оси в сторону, определяемую правилом правого винта.  Монет импульса твердого тела относительно оси есть сумма моментов импульса отдельных частиц:    Используя формулу v_i = ωr_i, получим    т. е.   2)  Таким образом, момент импульса твердого тела относительно оси равен моменту инерции тела относительно той же оси, умноженному на угловую скорость. Продифференцируем уравнение (2) по времени:    т. е.    Эта формула - еще одна форма уравнения динамики вращательного движения твердого тела относительно неподвижной оси: производная момента импульса твердого тела относительно оси равна моменту сил относительно той же оси.  Момент силы. Момент силы относительно точки  . Момент силы относительно неподвижной оси равен проекции вектора   на эту ось. Проекция вектора   на ось не зависит от положения точки, относительно которой определяется радиус-вектор силы   . Если вектор   лежит в плоскости перпендикулярной оси вращения, то проекция момента силы на ось равна произведению величины силы на плечо. Плечо силы — это длина перпендикуляра, опущенного на прямую, вдоль которой направлена сила.

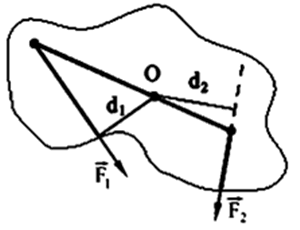
Определение моментов сил:  ,  .

№13 Момент инерции твердого тела.

Момент инерции — скалярная физическая величина, мера инертности во вращательном движении вокруг оси, подобно тому, как масса тела является мерой его инертности в поступательном движении. Характеризуется распределением масс в теле: момент инерции равен сумме произведений элементарных масс на квадрат их расстояний до базового множества (точки, прямой или плоскости).

Единица измерения СИ: кг·м².

Обозначение: I или J.

Различают несколько моментов инерции — в зависимости от многообразия, от которого отсчитывается расстояние точек.

Моментом инерции механической системы относительно неподвижной оси («осевой момент инерции») называется величина J_a, равная сумме произведений масс всех n материальных точек системы на квадраты их расстояний до оси:

,

где:

• m_i — масса i-й точки,

• r_i — расстояние от i-й точки до оси.

Осевой момент инерции тела J_a является мерой инертности тела вовращательном движении вокруг оси подобно тому, как масса тела является мерой его инертности в поступательном движении.

,

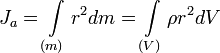где:

•  — масса малого элемента объёма тела  ,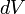

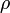•  — плотность,

•  — расстояние от элемента   до оси a.

Если тело однородно, то есть его плотность всюду одинакова, то

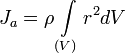
№14 Уравнение динамики твердого тела, вращающегося вокруг неподвижной оси.

Момент силы. Момент силы относительно точки  . Момент силы относительно неподвижной оси равен проекции вектора   на эту ось. Проекция вектора   на ось не зависит от положения точки, относительно которой определяется радиус-вектор силы   . Если вектор   лежит в плоскости перпендикулярной оси вращения, то проекция момента силы на ось равна произведению величины силы на плечо. Плечо силы — это длина перпендикуляра, опущенного на прямую, вдоль которой направлена сила.

Определение моментов сил:  ,  . Уравнение динамики твердого тела, вращающегося вокруг неподвижной оси: суммарный момент сил, действующих на тело, равен произведению момента инерции тела на угловое ускорение:  . Учитывая, что момент импульса твердого тела  , уравнение динамики твердого тела можно представить в виде .

№15 Момент инерции. Теорема Штейнера.

Момент инерции. Твердое тело можно представить в виде системы жестко связанных между собой материальных точек. Момент инерции системы материальных точек относительно оси вращения равен сумме произведений масс материальных точек системы на квадраты их расстояний до оси вращения: .

где:

• m_i — масса i-й точки,

• r_i — расстояние от i-й точки до оси.

Для расчета момента инерции используют интегрирование: .

Единица измерения СИ: кг·м².

Теорема Гюйгенса-Штейнера

Момент инерции твёрдого тела относительно какой-либо оси зависит не только от массы, формы и размеров тела, но также от положения тела по отношению к этой оси. Согласно теореме Штейнера (теореме Гюйгенса-Штейнера), момент инерции тела Jотносительно произвольной оси равен сумме момента инерции этого тела J_c относительно оси, проходящей через центр масс тела параллельно рассматриваемой оси, и произведения массы тела m на квадрат расстояния d между осями:

где   — полная масса тела.

№16 Кинетическая энергия вращающегося твердого тела (ось вращения неподвижна).

Кинетическая энергия тела, движущегося произвольным образом, равна сумме кинетических энергий всех n материальных точек па которые это тело можно разбить:

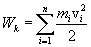
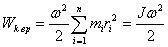Если тело вращается вокруг неподвижной оси с угловой скоростью  , то линейная скорость i-ой точки равна  , где  , - расстояние от этой точки до оси вращения. Следовательно.

где   - момент инерции тела относительно оси вращения.

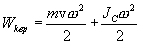В общем случае движение твердого тела можно представить в виде суммы двух движений - поступательного со скоростью, равной скорости   центра инерции тела, и вращения с угловой скоростью   вокруг мгновенной оси, проходящей через центр инерции. При этом выражение для кинетической энергии тела преобразуется к виду

где   - момент инерции тела относительно мгновенной оси вращения, проходящей через центр инерции.

№17 Работа, совершаемая при вращении твердого тела.

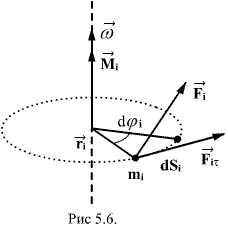
Рассмотрим действие внешней силы  , приложенной к точке массой  . За время  элементарная масса   проходит путь   Работа силы   на этом пути определяется проекцией силы на направление перемещения, которая очевидно, равна тангенциальной составляющей   силы.

Но   равна модулю момента   силы   относительно оси вращения. Работа  , и будет положительна, если   имеет такое же направление, как и   отрицательное, если направление векторов   и   противоположны.

С учетом, что 

Работа всех сил, приложенных к телу

Полная работа

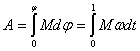
№18 Уравнение гармонических колебаний математического маятника.

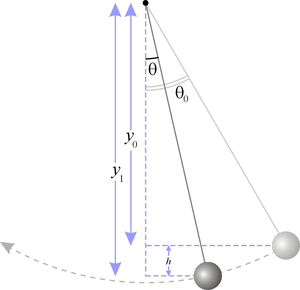
Математи́ческий ма́ятник — осциллятор, представляющий собоймеханическую систему, состоящую из материальной точки, находящейся на невесомой нерастяжимой нити или на невесомом стержне в однородном поле сил тяготения. Период малых собственных колебаний математического маятника длины L неподвижно подвешенного в однородном поле тяжести с ускорением свободного падения g равен

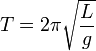
и не зависит от амплитуды и массы маятника.

Гармонические колебания

Маятник, совершающий малые колебания, движется по синусоиде. Поскольку уравнение движения является обыкновенным ДУ второго порядка, для определения закона движения маятника необходимо задать два начальных условия — координату и скорость, из которых определяются две независимых константы:

где   — амплитуда колебаний маятника,   — начальная фаза колебаний,   — циклическая частота, которая определяется из уравнения движения. Движение, совершаемое маятником, называется гармоническими колебаниями

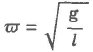
№19 Уравнение гармонических колебаний для физического маятника.

Физический маятник — это твердое тело, которое совершает колебания под действием силы тяжести вокруг неподвижной горизонтальной оси, которая проходит через точку О, не совпадающую с центром масс С тела (рис. 1). 

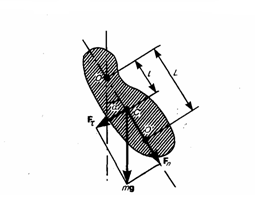
Рис.1

Если маятник из положения равновесия отклонили на некоторый угол α, то, используя уравнение динамики вращательного движения твердого тела, момент M возвращающей силы    где J — момент инерции маятника относительно оси, которая проходит через точку подвеса О, l – расстояние между осью и центром масс маятника, F_τ ≈ –mgsinα ≈ –mgα — возвращающая сила (знак минус указывает на то, что направления F_τ и α всегда противоположны; sinα ≈ α поскольку колебания маятника считаются малыми, т.е. маятника из положения равновесия отклоняется на малые углы). Уравнение запишем как    или    Принимая  получим уравнение      Из формулы вытекает, что при малых колебаниях физический маятник совершает гармонические колебания с циклической частотой ω₀ и периодом    где введена величина L=J/(ml) — приведенная длина физического маятника.

№20 Закон равного распределения энергии по степеням свободы в термодинамике.

Большинство химических веществ состоит из многоатомных молекул. Если рассматривать газообразное состояние вещества, то при столкновениях молекул тепловая энергия газа случайным образом расходуется на изменение кинетических энергий поступательного и вращательного движений молекул, а также на возбуждение колебаний атомов в молекуле. Естественно предположить, что указанные движения в молекуле могут происходить одновременно.

Средняя энергия приходящаяся на одну степень свободы:

У одноатомной молекулы i = 3, тогда для одноатомных молекул

для двухатомных молекул

для трёхатомных молекул

Таким образом, на среднюю кинетическую энергию молекулы, имеющей i-степеней свободы, приходится

Это и есть закон Больцмана о равномерном распределении средней кинетической энергии по степеням свободы.

Если система находится в состоянии термодинамического равновесия, при температуре Т, то средняя кинетическая энергия равномерно распределена между всеми степенями свободы. На каждую поступательную i_п и вращательную i_вр степени свободы приходится энергия 1/2 kT. Для колебательной i_кол, степени свободы она равна kT. Таким образом число степеней свободы i = i_п + i_вр + 2i_кол         Закон о равномерном распределении энергии по степеням свободы перестает быть справедливым при квантовом описании системы частиц, когда каждому квантовому состоянию системы с i-степенями свободы соответствует ячейка объемом hⁱ в фазовом пространстве “координаты – импульсы” тождественных (неразличимых между собой) частиц, где h – постоянная Планка (М. Планк (1858-1947) – немецкий физик–теоретик).