
1.
Алгебра логики.
Булева алгебра.
Булевы функции одной переменной.
Отрицание, дизъюнкция, конъюнкция, строгая дизъюнкция, импликация двух высказываний.
Таблица истинности
Булева алгебра служит основой для описания логики работы аппаратных и программных средств ЭВМ.
Алгебра логики использует логические переменные, которые принимают значения 0 и 1.
Рассмотрим
множество
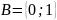 .
Отображение
.
Отображение
 назовем булевой
функцией n
переменных.
назовем булевой
функцией n
переменных.
Булевы функции одной переменной.
При n=1 существуют 4 булевы функции:
x |
|
|
|
|
0 |
0 |
0 |
1 |
1 |
1 |
0 |
1 |
0 |
1 |


тождественный нуль тождественная единица
Высказывание – это утверждение, о котором можно сказать истинно оно или ложно.
Высказывания обозначаются латинскими буквами строчными или прописными, также можно использовать индексы.
Отрицанием,
или
инверсией,
высказывания
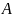 называется
высказывание
называется
высказывание
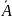 ,
которое истинно, когда высказывание
ложно, и ложно, когда
истинно.
,
которое истинно, когда высказывание
ложно, и ложно, когда
истинно.
Дизъюнкцией
(нестрогой или соединительной) высказываний
и
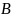 называется высказывание
называется высказывание
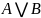 ,
которое истинно тогда и только тогда,
когда истинно
хотя бы одно из этих высказываний.
,
которое истинно тогда и только тогда,
когда истинно
хотя бы одно из этих высказываний.
Конъюнкцией
высказываний
и
называется высказывание
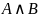 ,
которое истинно тогда и только тогда,
когда истинны
оба высказывания.
,
которое истинно тогда и только тогда,
когда истинны
оба высказывания.
Строгой
дизъюнкцией
высказываний
и
называется высказывание
 (
(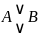 ),
которое истинно тогда и только тогда,
когда истинно
только одно из этих высказываний.
),
которое истинно тогда и только тогда,
когда истинно
только одно из этих высказываний.
Импликацией
высказываний
и
называется высказывание
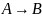 ,
которое ложно тогда и только тогда,
когда из
истины следует ложь.
,
которое ложно тогда и только тогда,
когда из
истины следует ложь.
Эквиваленцией
высказываний
и
называется высказывание
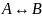 ,
которое истинно тогда и только тогда,
когда либо истинны, либо ложны одновременно
оба высказывания.
,
которое истинно тогда и только тогда,
когда либо истинны, либо ложны одновременно
оба высказывания.
2.
Алгебра логики.
Булева алгебра.
Булевы функции двух переменных.
Таблица истинности
Булева алгебра служит основой для описания логики работы аппаратных и программных средств ЭВМ.
Алгебра логики использует логические переменные, которые принимают значения 0 и 1.
Рассмотрим множество . Отображение назовем булевой функцией n переменных.
Булевы функции двух переменных.
При n=2 существуют 16 булевых функций:
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
0 |
1 |
0 |
0 |
0 |
0 |
1 |
1 |
1 |
1 |
0 |
0 |
0 |
0 |
1 |
1 |
1 |
1 |
1 |
0 |
0 |
0 |
1 |
1 |
0 |
0 |
1 |
1 |
0 |
0 |
1 |
1 |
0 |
0 |
1 |
1 |
1 |
1 |
0 |
1 |
0 |
1 |
0 |
1 |
0 |
1 |
0 |
1 |
0 |
1 |
0 |
1 |
0 |
1 |
Эти функции можно разделить на 3 группы:
1)симметрические функции:
– конъюнкция, , логич. умножение, логич. И;
– дизъюнкция,
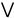 ,
логич. сложение, логич. ИЛИ;
,
логич. сложение, логич. ИЛИ;
– эквиваленция, (одинаковые – 1; разные – 0);
– сумма
по модулю 2,
 ,
строгая дизъюнкция,
,
строгая дизъюнкция,
 ;
;
– стрелка Пирса, - является отрицанием дизъюнкции;
– штрих Шеффера, | - является отрицанием конъюнкции.
Все эти функции симметричны по аргументам.
2)импликации (следования)
– (из правды – ложь ложь)
3)функции, явно зависящие от одной переменной
, , ,
1, 16 нуль и единица
3, 5, 12 – ?
3.
Законы логики.
Равносильные преобразования
Равносильности формул логики называют законами логики. Знание законов логики позволяет проверять правильность рассуждений и доказательств.
Законы логики
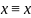 закон
тождества
закон
тождества
 закон
противоречия
закон
противоречия
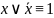 закон
исключенного третьего
закон
исключенного третьего
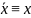 закон
двойного отрицания
закон
двойного отрицания

закон идемпотентности
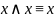
закон коммутативности (переместительный)
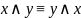
закон ассоциативности
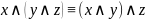
закон дистрибутивности
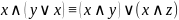
законы де Моргана
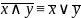
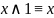

законы поглощения

законы склеивания
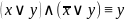
Расшифровка первых пяти:
1. I закон сформулирован Аристотелем. Закон утверждает, что мысль, заключённая в некотором высказывании, остаётся неизменной на протяжении всего рассуждения, в котором это высказывание фигурирует.
2. Закон противоречия говорит о том, что никакое предложение не может быть истинно одновременно со своим отрицанием.
3.Этот закон говорит о том, что для каждого высказывания имеются лишь две возможности: это высказывание либо истинно, либо ложно, третьего не дано.
4. Закон двойного отрицания. Отрицать отрицание высказывания – то же, что и утверждать это высказывание.
5. Законы идемпотентности. В алгебре логики нет показателей степеней и коэффициентов. Конъюнкция (дизъюнкция) одинаковых сомножителей равносильна одному из них.
Доказать законы логики можно с помощью:
таблиц истинности;
равносильных преобразований.
Равносильные преобразования?
4.
Минимизация булевых функций.
Дизъюнктивная нормальная форма.
Совершенная дизъюнктивная нормальная форма
Минимизация булевых функций – замена громоздких булевых функций им равносильными, но более простыми, используя законы алгебры логики.
Минимизировать булевы функции надо, приводя их к так называемой нормальной форме.
Существуют две разновидности нормальных форм – дизъюнктивная (ДНФ) и конъюнктивная (КНФ).
Элементарной
конъюнкцией
(ЭК) называется выражение, состоящее из
конечного числа переменных и их отрицаний,
взятых в этом выражении не более одного
раза и разделенных операциями конъюнкции.
Например,
 .
.
Дизъюнктивной нормальной формой (ДНФ) называется дизъюнкция конечного числа элементарных конъюнкций.
Дизъюнктивная нормальная форма называется совершенной, если в каждой ее элементарной конъюнкции представлены все переменные, входящие в данную функцию (либо сами, либо с отрицанием). Сокращенно СДНФ.
ВСЁ?
5.
Минимизация булевых функций.
Конъюнктивная нормальная форма.
Совершенная конъюнктивная нормальная форма
Минимизация булевых функций – замена громоздких булевых функций им равносильными, но более простыми, используя законы алгебры логики.
Минимизировать булевы функции надо, приводя их к так называемой нормальной форме.
Существуют две разновидности нормальных форм – дизъюнктивная (ДНФ) и конъюнктивная (КНФ).
Элементарной
дизъюнкцией
(ЭД) называется выражение, состоящее из
конечного числа переменных и их отрицаний,
взятых в этом выражении не более одного
раза и разделенных операциями дизъюнкции.
Например,
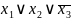 .
.
Конъюнктивной нормальной формой (КНФ) называется конъюнкция конечного числа элементарных дизъюнкций.
Конъюнктивная нормальная форма называется совершенной, если в каждой ее элементарной дизъюнкции представлены все переменные, входящие в данную функцию (либо сами, либо с отрицанием). Сокращенно СКНФ.
ВСЁ?
6.
Минимизация булевых функций.
Приведение ДНФ к СДНФ, к КНФ
Минимизация булевых функций – замена громоздких булевых функций им равносильными, но более простыми, используя законы алгебры логики.
Минимизировать булевы функции надо, приводя их к так называемой нормальной форме.
Существуют две разновидности нормальных форм – дизъюнктивная (ДНФ) и конъюнктивная (КНФ).
Чтобы привести ДНФ к СДНФ, нужно дополнить ЭК на множитель, содержащий недостаточную переменную и ее отрицание.
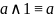
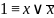
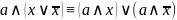
КАК К КНФ?
7.
Минимизация булевых функций.
Приведение КНФ к СКНФ, к ДНФ
Минимизация булевых функций – замена громоздких булевых функций им равносильными, но более простыми, используя законы алгебры логики.
Минимизировать булевы функции надо, приводя их к так называемой нормальной форме.
Существуют две разновидности нормальных форм – дизъюнктивная (ДНФ) и конъюнктивная (КНФ).
Чтобы привести КНФ к СКНФ нужно добавить в неполную ЭД слагаемое, содержащее конъюнкцию недостающей переменной и ее отрицания.
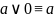

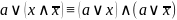
КАК К ДНФ?
8.
Логика предикатов
Предикатом называется сказуемое суждения, т.е. то, что утверждается или отрицается относительно объекта этого суждения.
«Он получил специальность программиста» - пример предиката.
Предикат становится высказыванием, если вместо местоимения подставить конкретный объект.
«М. А. Иванов стал программистом» (истина).
Язык логики предикатов
Символами
X,
Y,
Z,
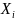 ,
,
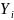 … в логике предикатов принято обозначать
предметные переменные, т.е. отдельные
предметы – имена. Они могут быть простыми
или сложными. Если такие предметы (имена)
не содержат дополнительной информации
о себе, то они называются собственными
(простыми), например, «земля», «студент»
и др.
… в логике предикатов принято обозначать
предметные переменные, т.е. отдельные
предметы – имена. Они могут быть простыми
или сложными. Если такие предметы (имена)
не содержат дополнительной информации
о себе, то они называются собственными
(простыми), например, «земля», «студент»
и др.
Если такое имя содержит наряду с самим предметом его отдельные свойства, то оно является сложным, например «перпендикулярные прямые», «автор романа «Анна Каренина»» и др.
Рассмотрим предикат
x y+2
y+2
где
x
определен на множестве
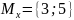
y
– на множестве

Сравним
предикаты
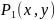 и
и
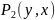
|
x y+2 |
|
|
|
|
(3;1) |
3 1+2 |
1 |
(1;3) |
1 3+2 |
0 |
(3;5) |
3 5+2 |
0 |
(1;5) |
1 5+2 |
0 |
(3;8) |
3 8+2 |
0 |
(5;3) |
5 3+2 |
1 |
(5;1) |
5 1+2 |
1 |
(5;5) |
5 5+2 |
0 |
(5;5) |
5 5+2 |
0 |
(8;3) |
8 3+2 |
1 |
(5;8) |
5 8+2 |
0 |
(8;5) |
8 5+2 |
1 |
Одноместный предикат называется предикатом-свойством.
Двухместный и более предикат называется предикатом-отношением.
0-местный предикат называется высказыванием.
Полный прообраз единицы при предикате P называется множеством истинности предиката.
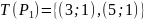

Если множество истинности предиката совпадает с его областью определения, то такой предикат называется тождественно истинным. И тождественно ложным, если множество истинности предиката пустое.
9.
Кванторы всеобщности и существования.
Построение операций к предикатам
Для
количественных характеристик обычно
используют понятия «все», «некоторые»,
«существуют» и др., которые называют
кванторами
(от
лат. quantum
– сколько). Мы часто пользовались
символами
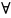 и
и
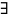 ,
заменяющими слова «любой» и «существует».
Покажем действие этих кванторов в
высказывательных формах. Часть формулы,
на которую распространяется действие
квантора, называется областью действия
этого квантора. Вхождение переменной
в формулу может быть связанным , если
переменная расположена либо непосредственно
после знака квантора, либо в области
действий квантора, после которого стоит
переменная. Все прочие вхождения –
свободные. Например, в выражении
,
заменяющими слова «любой» и «существует».
Покажем действие этих кванторов в
высказывательных формах. Часть формулы,
на которую распространяется действие
квантора, называется областью действия
этого квантора. Вхождение переменной
в формулу может быть связанным , если
переменная расположена либо непосредственно
после знака квантора, либо в области
действий квантора, после которого стоит
переменная. Все прочие вхождения –
свободные. Например, в выражении
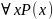 переменная x
связывает свойства предиката и квантор
общности.
переменная x
связывает свойства предиката и квантор
общности.
- для любого x верно P(x)
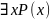 -
существует x,
для которого выполняется P(x).
-
существует x,
для которого выполняется P(x).
10.
Множества.
Задание множеств
Совокупность элементов, объединенных некоторым признаком, свойством, составляет понятие множество. Например, множество книг в библиотеке, множество студентов в группе, множество натуральных чисел N и т.д.
Запись
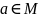 означает: элемент a
принадлежит
множеству
M,
т.е. элемент a
обладает некоторым признаком. Аналогично
означает: элемент a
принадлежит
множеству
M,
т.е. элемент a
обладает некоторым признаком. Аналогично
 читвется так: элемент a
не
принадлежит
множеству М.
читвется так: элемент a
не
принадлежит
множеству М.
Множество считается заданным, если или перечислены все его элементы, или указано свойство, которым обладают те и только те элементы, которые принадлежат данному множеству.
Первый
вариант записывается так:
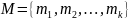 ,
например, M={0;1}.
,
например, M={0;1}.
Последний
вариант записывается так: M={b|P(b)}.Такая
запись читается так: M
состоит из тех (всех) элементов b,
которые обладают признаком P.
Например, M={n|n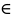 N,n<5}
означает: М составляют только те
натуральные числа, что меньше пяти.
N,n<5}
означает: М составляют только те
натуральные числа, что меньше пяти.
Само свойство Р будем называть характеристикой.
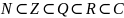

нат. цел. рацион. действ. компл.
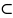 -
включение (для двух множеств)
-
включение (для двух множеств)
Изображение множеств
Диаграммы Эйлера-Венна
A
B
C
R
Q
Z
N
Множество K называется подмножеством множества M если x K x M.
Универсальным называют множество U, состоящее из всех возможных элементов, обладающих данным признаком.
U = {Меркурий, Венера, Земля, Марс, Юпитер, Сатурн, Уран, Нептун, Плутон}
Равными называют два множества А и В, состоящие из одинаковых элементов: А=В.
Например,
равны множества решений уравнений
4x-8=16,
x/15=2/5
и
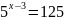 ,
т.к. их решением будет являться одно и
то же число 6.
,
т.к. их решением будет являться одно и
то же число 6.
Множество
не содержащее элементы, которое обладают
данным признаком, называется пустым,
обозначается
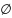 .
.
Мощность – число элементов множества А, обозначается |А| или n(A).
|U| = 9
| |=0
11.
Множества.
Операции над множествами
A = {1, 2, 3, 4, 6}
B = {1, 3, 5, 7}
Существуют 4 вида операций:

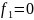
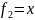
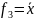


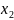
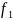 0
0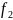

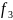

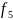

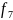
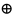
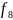
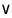
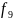

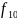
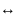
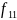
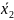
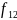

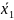
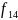

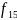 |
| 1
1

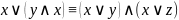


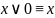


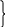
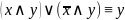
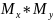

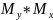
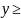 x+2
x+2