Заключение

Зачастую, теме «Правильные многогранники» уделяется не слишком пристальное внимание на школьных уроках. Считается, что данная тема является лишь одним из аспектов математики и не имеет практического применения. В своей работе я постарался опровергнуть данное суждение, посвятив практическому применению Платоновых тел одну из глав своего проекта. На мой взгляд, данная тема далеко не является узкопрофильной – на протяжении работы над проектом я постоянно натыкался на стыки данной темы с другими областями знаний – алгебры, биологии, географии, искусства и живописи.

Обобщая научную информацию по обозначенной проблеме, можно сформулировать следующие выводы:

1. В исследованиях правильных многогранников можно проследить два основных этапа:

I этап: Исследования до н.э.

II этап: исследования в XVI – XIX вв.

2. На первом этапе главным содержанием стала 13 книга «Начал» Евклида, а которой ему не удалось решить проблему построения правильных многогранников, но удалось дать им первоначальную характеристику и теоретическое обоснование.

3. В рамках второго этапа исследований была сформулирована пусть и ошибочная гипотеза Кеплера, кроме того была решена проблема построения правильных многогранников.

4. Можно проследить следующую особенность: на каждом этапе вначале выдвигались неверные теории, которые впоследствии вели к открытиям

5. Разрыв между первым и вторым этапом составляет ни много ни мало полторы тысячи лет – разумно предположить, что в это время еще не существовало возможности для создания теорий в области Платоновых тел

Приложение №1

«Элементы теории правильных многогранников»

Тетраэдр и его свойства

• Тетраэдр составлен из четырех равносторонних треугольников.

• Каждая его вершина является вершиной трех треугольников.

• Сумма плоских углов при каждой вершине равна 180 градусов.

Таким образом,

тетраэдр имеет

4 грани,

4 вершины

и 6 ребер.

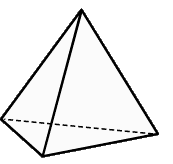
• Тетраэдр не имеет центра симметрии, но имеет 3 оси симметрии и 6 плоскостей симметрии.

• Радиус описанной сферы:

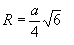
• Радиус вписанной сферы:

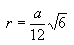
• Площадь поверхности:

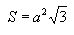
• Объем тетраэдра:

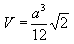
Гексаэдр и его свойства

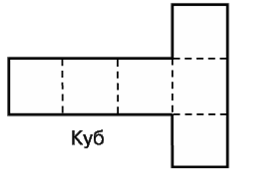
• Куб составлен из шести квадратов.

• Каждая его вершина является вершиной трех квадратов.

• Сумма плоских углов при каждой вершине равна 270 градусов.

Таким образом, куб имеет

6 граней,

8 вершин

12 ребер.

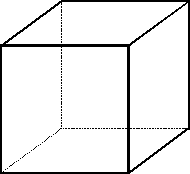
• Куб имеет центр симметрии - центр куба, 9 осей симметрии и 9 плоскостей симметрии.

• Радиус описанной сферы:

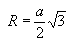
• Радиус вписанной сферы:

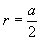
• Площадь поверхности куба: S = 6a²

• Объем куба: V = a³

Октаэдр и его свойства

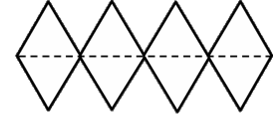
• Октаэдр составлен из восьми равносторонних треугольников.

• Каждая его вершина является вершиной четырех треугольников.

• Сумма плоских углов при каждой вершине равна 240 градусов.

Таким образом,

октаэдр имеет

8 граней,

6 вершин

12 ребер.

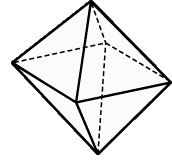
• Октаэдр имеет центр симметрии - центр октаэдра, 9 осей симметрии и 9 плоскостей симметрии.

• Радиус описанной сферы:

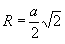
• Радиус вписанной сферы:

• Площадь поверхности:

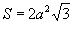
• Объем октаэдра:

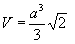
Икосаэдр и его свойства

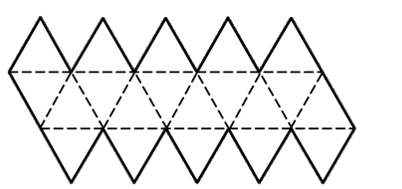
• Икосаэдр составлен из двадцати равносторонних треугольников.

• Каждая его вершина является вершиной пяти треугольников.

• Сумма плоских углов при каждой вершине равна 300 градусов.

Таким образом,

икосаэдр имеет

20 граней,

12 вершин

30 ребер.

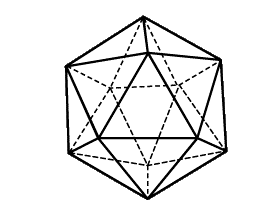
• Икосаэдр имеет центр симметрии - центр икосаэдра, 15 осей симметрии и 15 плоскостей симметрии.

• Радиус описанной сферы:

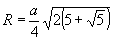
• Радиус вписанной сферы:

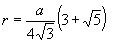
• Площадь поверхности:

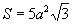
• Объем икосаэдра:

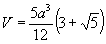
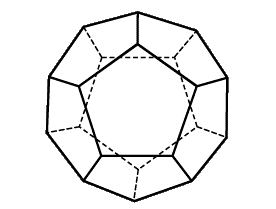
Додекаэдр и его свойства

• Додекаэдр составлен из двенадцати равносторонних пятиугольников.

• Каждая его вершина является вершиной трех пятиугольников.

• Сумма плоских углов при каждой вершине равна 324 градусов.

• Таким образом,

додекаэдр имеет

12 граней,

20 вершин

30. ебер.

• Радиус описанной сферы:

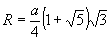
• Радиус вписанной сферы:

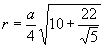
• Площадь поверхности:

• Объем додекаэдра:

Приложение №2

«Исследования правильных многогранников в период до нашей эры

»

Евклид Платон

Приложение №3

Исследования правильных многогранников в XVI – XIX вв.

Леонард Эйлер Иоганн Кеплер

Звёздчатый многогранник — это правильный невыпуклый многогранник. Многогранники из-за их необычных свойств симметрии исследуются с древнейших времён. Также формы многогранников широко используются в декоративном искусстве.

Звездчатые многогранники очень декоративны, что позволяет широко применять их в ювелирной промышленности при изготовлении всевозможных украшений. Применяются они и в архитектуре. Многие формы звездчатых многогранников подсказывает сама природа. Снежинки — это звездчатые многогранники. С древности люди пытались описать все возможные типы снежинок, составляли специальные атласы. Сейчас известно несколько тысяч различных типов снежинок. Есть много видов звёздчатых многогранников. Наиболее известные это:

1 Звёздчатый октаэдр 2 Додекаэдр 3 Икосаэдр 4 Икосододекаэдр

Приложение №4

Правильные многогранники в нашей жизни

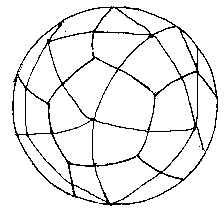
икосаэдрово-додекаэдровая сетка