Вопрос 3
Вычисление
напряженности поля большой системы
электрических зарядов с помощью принципа
суперпозиции электростатических полей
можно существенно упростить, используя
теорему Гаусса. Эта теорема определяет
поток вектора напряженности
электрического поля через произвольную
замкнутую поверхность. Для произвольной
замкнутой поверхности S поток вектора
напряженности
через
эту поверхность определяется выражением
(1.23)
где
проекция
вектора
на
нормаль
к
площадке dS (рис. 1.10);
вектор,
модуль которого равен dS, а направление
совпадает с направлением нормали к
площадке (
).
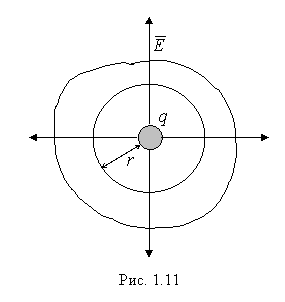
Рассмотрим сферическую
поверхность радиуса r, охватывающую
точечный заряд q, находящийся в ее
центре (рис. 1.11). В соответствии с формулой
(1.23) поток вектора напряженности сквозь
эту поверхность будет равен:
(1.24)
Этот
результат справедлив для замкнутой
поверхности любой формы: если окружить
рассматриваемую сферу произвольной
замкнутой поверхностью, то каждая линия
напряженности, пронизывающая сферу,
пройдет и сквозь эту поверхность.
Рассмотрим теперь общий случай
произвольной замкнутой поверхности,
окружающей n зарядов. В соответствии
с принципом суперпозиции напряженность
поля,
создаваемого всеми зарядами, равна
векторной сумме напряженностей
полей,
обусловленных каждым зарядом в
отдельности; поэтому поток вектора
напряженности результирующего поля
будет равен:
Согласно
(1.24) каждый из интегралов, стоящий под
знаком суммы, равен
.
Следовательно,
(1.25)
т.е.
поток вектора напряженности
электростатического поля в вакууме
сквозь произвольную замкнутую поверхность
равен алгебраической сумме заключенных
внутри этой поверхности зарядов, деленной
на электрическую постоянную.
Применим теорему Гаусса для определения
напряженности поля равномерно заряженной
бесконечной плоскости. В этом случае
ее поверхностная плотность заряда
одинакова в любом месте плоскости. Это означает, что линии напряженности перпендикулярны плоскости в любой точке, т.е. поле заряженной плоскости однородно (рис. 1.12).
В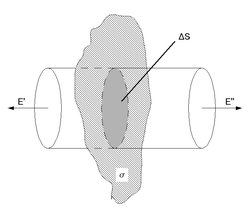
опрос
4
Для вычисления электромагнитных полей используются следующие величины:
Объёмная плотность заряда (см. выше).
Поверхностная плотность заряда
,
где dS — бесконечно малый участок поверхности.
Линейная плотность заряда
,
где dl — длина бесконечно малого отрезка.
Расчёт напряжённости бесконечной плоскости
Рассмотрим
поле, создаваемое бесконечной однородной
заряженной плоскостью. Пусть поверхностная
плотность заряда плоскости одинакова
и равна σ. Представим себе мысленно
цилиндр с образующими, перпендикулярными
к плоскости, и основанием ΔS, расположенным
относительно плоскости симметрично. В
силу симметрии
.
Поток вектора напряжённости равен
.
Применив теорему Гаусса, получим:
,из
которого
,
Расчёт
напряжённости бесконечной нити
Рассмотрим
поле, создаваемое бесконечной нитью с
линейной плотностью заряда, равной λ.
Пусть требуется определить напряжённость,
создаваемую этим полем на расстоянии
R от нити. Возьмём в качестве Гауссовой
поверхности цилиндр с осью, совпадающей
с нитью, радиусом R и высотой Δl. Тогда
поток напряжённости через эту поверхность
рассчитывается следующим образом:
В силу симметрии, модуль напряжённости в любой точке поверхности цилиндра будет одинаков. Тогда поток напряжённости через эту поверхность рассчитывается следующим образом:
Учитывается только площадь боковой поверхности цилиндра, так как поток через основания цилиндра равен нулю. Приравнивая 1 и 2 выражения, получим:
