Вопрос 17

Вопрос 18

З ако́н Ома — это физический закон, определяющий связь между напряжением, силой тока и сопротивлением проводника в электрической цепи. Назван в честь его первооткрывателя Георга Ома. Суть закона проста: сила тока в проводнике прямо пропорциональна напряжению между концами проводника, если при прохождении тока свойства проводника не изменяются. Следует также иметь в виду, что закон Ома является фундаментальным и может быть применён к любой физической системе, в которой действуют потоки частиц или полей, преодолевающие сопротивление. Его можно применять для расчёта гидравлических, пневматических, магнитных, электрических, световых, тепловых потоков и т. д., также, как и Правила Кирхгофа, однако, такое приложение этого закона используется крайне редко в рамках узко специализированных расчётов.

Закон Ома формулируется так: Сила тока в однородном участке цепи прямо пропорциональна напряжению, приложенному к участку, и обратно пропорциональна характеристике участка, которую называют электрическим сопротивлением этого участка.

Закон Ома в интегральной форме

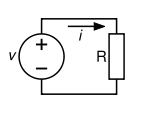
Схема, иллюстрирующая три составляющие закона Ома

Диаграмма, помогающая запомнить закон Ома. Нужно закрыть искомую величину, и два других символа дадут формулу для её вычисления

Закон Ома для участка электрической цепи имеет вид:

где:

U — напряжение или разность потенциалов, I — сила тока, R — сопротивление. Закон Ома также применяется ко всей цепи,но в несколько изменённой форме: ,где: — ЭДС цепи, I — сила тока в цепи, R — сопротивление всех элементов цепи, r — внутреннее спротивление источника питания. Закон Ома в дифференциальной форме

Сопротивление R зависит как от материала, по которому течёт ток, так и от геометрических размеров проводника. Полезно переписать закон Ома в так называемой дифференциальной форме, в которой зависимость от геометрических размеров исчезает, и тогда закон Ома описывает исключительно электропроводящие свойства материала. Для изотропных материалов имеем:

где:

— вектор плотности тока,

σ — удельная проводимость,

— вектор напряжённости электрического поля.

Все величины, входящие в это уравнение, являются функциями координат и, в общем случае, времени. Если материал анизотропен, то направления векторов плотности тока и напряжённости могут не совпадать. В этом случае удельная проводимость является тензором ранга (1, 1).

Раздел физики, изучающий течение электрического тока в различных средах, называется электродинамикой сплошных сред.

Закон Ома для переменного тока

Если цепь содержит не только активные, но и реактивные компоненты (ёмкости, индуктивности), а ток является синусоидальным с циклической частотой ω, то закон Ома обобщается; величины, входящие в него, становятся комплексными:

где: U = U0eiωt — напряжение или разность потенциалов,

I — сила тока,

Z = Re—iδ — комплексное сопротивление (импеданс),

R = (Ra2+Rr2)1/2 — полное сопротивление,

Rr = ωL — 1/ωC — реактивное сопротивление (разность индуктивного и емкостного),

Rа — активное (омическое) сопротивление, не зависящее от частоты,

δ = —arctg Rr/Ra — сдвиг фаз между напряжением и силой тока.

При этом переход от комплексных переменных в значениях тока и напряжения к действительным (измеряемым) значениям может быть произведён взятием действительной или мнимой части (но во всех элементах цепи одной и той же!) комплексных значений этих величин. Соответственно, обратный переход строится для, к примеру, U = U0sin(ωt + φ) подбором такой , что . Тогда все значения токов и напряжений в схеме надо считать как

Если ток изменяется во времени, но не является синусоидальным (и даже периодическим), то его можно представить как сумму синусоидальных Фурье-компонент. Для линейных цепей можно считать компоненты фурье-разложения тока действующими независимо.

Также необходимо отметить, что закон Ома является лишь простейшим приближением для описания зависимости тока от разности потенциалов и для некоторых структур справедлив лишь в узком диапазоне значений. Для описания более сложных (нелинейных) систем, когда зависимостью сопротивления от силы тока нельзя пренебречь, принято обсуждать вольт-амперную характеристику. Отклонения от закона Ома наблюдаются также в случаях, когда скорость изменения электрического поля настолько велика, что нельзя пренебрегать инерционностью носителей заряда.

Объяснение закона Ома

Закон Ома можно просто объяснить при помощи теории Друде

Вопрос 19

Вопрос 20

Вопрос 21

Вопрос 22.

  Почти сто лет тому назад П.Друде разработал теорию электро- и теплопроводности металлов. В теории Друде валентные электроны металла рассматривались как классический "электронный" газ (идеальный газ из электронов). Применение к этой модели основных положений элементарной молекулярно-кинетической теории привело к поразительным результатам. На основе этих представлений оказалось возможным объяснить закон Видемана-Франца, объяснить эффект Холла, возникновение контактной разности потенциалов, явление термоэлектронной эмиссии. Для всех перечисленных явлений удалось получить количественные зависимости между величинами, определяющими то или иное явление. Теория Друде не свободна от внутренних противоречий. Современная физика твердого тела базируется на представлениях квантовой механики, а для описания свойств электронного газа используется квантовая статистика, отличная от статистики Максвелла - Больцмана. Вместе с тем теория Друде не потеряла своей полезности: отдельные ее результаты поражают своей точностью, а методы теории Друде на редкость физически наглядны.

      В рамках элементарной кинетической теории полагаем, что валентные электроны (электроны проводимости) металлов представляют собой одинаковые твердые сферы, двигаются они по прямым линиям до столкновения друг с другом, время контакта частиц пренебрежимо мало по сравнению с временем "свободного" движения.

      Объемную концентрацию электронов проводимости можно оценить выражением: (6.30) Где - объемная плотность металла (кг/м³), Z - валентность химического элемента, N_a - число Авогадро, А - относительная атомная масса элемента.

      Заряд электрона е =-1,6*10^-19 Кл, масса электрона m_e = 0,91*10^-30 кг. Величину "е" ниже будем считать положительной, а знак заряда электрона будем учитывать непосредственно в формулах.

      Плотность электронного газа: (6.31)     значительно больше плотности обычных газов при нормальных условиях.

      В теории Друде пренебрегают сильным электрон-электронным и электрон-ионным взаимодействием, полагая, что внутри металлического тела отдельный электрон практически ведет себя как свободная частица. Это дает нам право считать электрон "нейтральной" частицей при расчете взаимодействия ее с остальными частицами, но способной переносить заряд при расчете параметров электрического тока. Рис. 6.1.      П.Друде полагал, что электроны в своем движении сталкиваются с атомами (ионами) кристаллической структуры металла (столкновения электрон-электрон значительно менее вероятны). Картина последовательных соударений электрона с атомами кристаллической решетки показана на рис. 6.1.

     Современная теория оценивает вероятность такого механизма не очень высоко: рассеяние электронов имеет и другие механизмы. Поэтому не следует наглядную картину рис.6.1 понимать в буквальном смысле. Будем считать, что отношение (6.32)     представляет собой вероятность соударения электрона с рассеивающим центром, где dt - промежуток времени, - время релаксации или время свободного пробега. Предполагается, что величина не зависит от пространственного положения электрона и не меняется от соударения к соударению. Предполагается также, что электроны находятся в состоянии теплового равновесия со своим окружением. Механизм соударения детализируется следующим образом: скорость электрона после соударения статистически не связана со скоростью электрона до соударения (электрон "забыл" свою предысторию), направление скорости после соударения - случайное, хаотическое, а ее величина соответствует той температуре, которая имеет место в окрестности точки соударения.