1. Теория множеств и булева алгебра.
Понятие множества принимается за одно из исходных (аксиоматических) понятий. Теория множеств - раздел математики, в котором изучаются общие свойства множеств. Лежит в основе большинства математических дисциплин.
Над множествами определены следующие операции:
-
объединение
(или сумма) (обозначается
как
);
Это множество, содержащее в себе все
элементы исходных множеств. Объединение
двух множеств A
и В обычно обозначается
,
иногда - в виде суммы. Операция объединения
множеств коммутативна
(переместительность (2+3=3+2)):
Операция объединения множеств ассоциативна
(2+3)+5=2+(3+5):
Пустое
множество Х
явл-ся нейтральным
эл-том операции объединения множеств:
Пример:
-
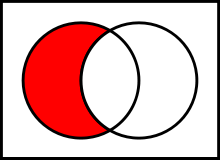разность
(обозначается как
реже
);
Это теоретико-множественная операция,
результатом которой является множество,
в которое входят все элементы первого
множества, не входящие во второе
множество. Пусть А и В - два указанных в
определении множества, тогда их разность
определяется
Это множество часто называют дополнением
множества В до множества А. (только когда
множество В полностью принадлежит
множеству А) (обозначается как
или
);
-
пересечение
(или произведение) (обозначается как
);
Это множество, которому принадлежат те
и только те элементы, которые одновременно
принадлежат всем данным множествам.
Пусть даны два множества А и Б. Тогда их
пересечением называется множество
Операция пересечения множеств
коммутативна:
Операция пересечения множеств
ассоциативна:
Если
- пустое множество (множество, не
содержащее ни одного элемента), то
Пример:
Тогда
-
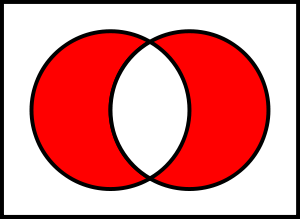симметрическая
разность
(обозначается как
реже
).
Это множественная операция, результатом
которой является множество элементов
этих множеств, принадлежащих только
одному из них. Симметрическая разность
двух заданных множеств А и В - это такое
множество
,
куда входят все те элементы первого
множества, которые не входят во второе
множество, а, также те элементы второго
множества, которые не входят в первое
множество:
Симметрическая разность коммутативна:
Симметрическая разность ассоциативна:
.
Пример:
Тогда
Б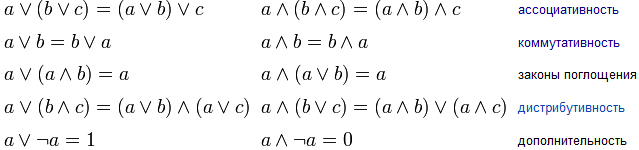
улева
алгебра
- непустое множество A с двумя бинарными
операциями (операция, принимающая два
аргумента и возвращающая один результат)
(аналог конъюнкции (И)),
(аналог дизъюнкции (ИЛИ)), унарной
операцией
(для унарной операции «–» результат её
применения к элементу х записывается
в виде-х.) (аналог отрицания) и двумя
выделенными элементами: 0 (или Ложь) и 1
(или Истина) такими, что для всех a, b и c
из множества A верны следующие аксиомы
(рисунок).
Основные законы булевой алгебры:
- закон двойного отрицания: not not x = x.
- закон коммутативности (от перестановки аргументов результат не меняется): x1 or x2 = x2 or x1. x1 and x2 = x2 and x1
- закон ассоциативности (порядка вычислений): x1 or (x2 or x3) = (x1 or x2) or x3. x1 and (x2 and x3) = (x1 and x2) and x3
- закон дистрибутивн-ти (раскрытия скобок): x1 or (x2 and x3) = (x1 or x2) and (x1 or x3). x1 and (x2 or x3) = (x1 and x2) or (x1 and x3)
- правила де Моргана: not (x1 or x2) = not x1 and not x2. not (x1 and x2) = not x1 or not x2
- правила операций с константами 0 и 1: not 0 = 1, not 1 = 0, x or 0 = x, x or 1 = 1, x and 1 = x, x and 0 = 0
- правила операций с переменной и её инверсией: x or not x = 1. x and not x = 0.
x
1 x2 and or xor
0 0 0 0 0
0 1 0 1 1
1 0 0 1 1
1 1 1 1 0
Хor называется "сложение по модулю 2". В двоичной системе 0+0=0, 0+1=1+0=1, 1+1=10, а по модулю 2 (остаток от деления на 2) последняя сумма и даёт 0.