§49. Построение областей устойчивости на эвм

При использовании ЭВМ в принципе применим метод D- разбиения, однако наибольшее применение получил критерий Рауса.

Задача расчета при этом разбивается на два этапа:

1) Определение коэффициентов характеристического уравнения;

2)Нахождение распределения корней относительно мнимой оси.

Коэффициенты характеристического уравнения находятся по известному векторно-матричному уравнению состояния . Выше было получено характеристическое уравнение для такого матричного описания в общем виде det или

.

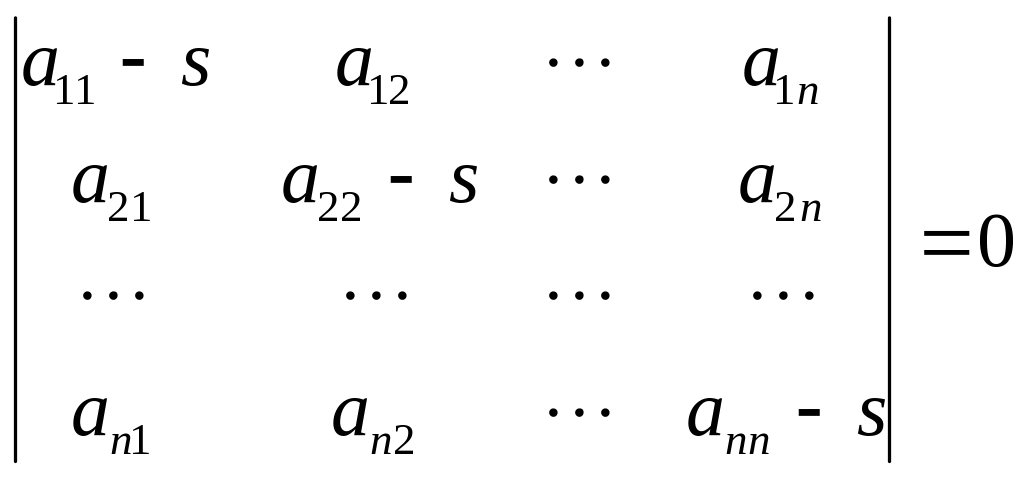Т.к раскрытие определителя высокого порядка представляет собой сложную вычислительную задачу, то обычным путем она не решается.

Искомое характеристическое уравнение в виде находится с применением специальных расчетных методов.

Его корни называются собственными числами матрицы А, а все множество из n корней образует спектр матрицы А.

Коэффициент характеристического уравнения равен сумме диагональных миноров первого порядка, эта сумма называется следом матрицы А и обозначается .

Коэффициент характеристического уравнения равен сумме диагональных миноров второго порядка матрицы А; коэффициент равен определителю матрицы А , т.е. .

Однако и такой способ нахождения коэффициентов неприемлем с вычислительной точки зрения. Практическое применение получили два метода.

Метод Данилевского предполагает приведение характеристической матрицы к

так называемому виду Фробениуса :

После приведения к такому виду коэффициенты характеристического уравнения становятся известными по первой строке. Недостаток метода - в вырождении промежуточных определителей (т.е. близости их нулю).

Второй метод лишен этого недостатка и носит название Леверье-Фаддеева.

Он предполагает выполнение следующей рекуррентной процедуры для вычисления коэффициентов:

… … … … … … … … … … … … … … …

При построении области устойчивости по двум параметрам эта процедура вычисления коэффициентов должна быть произведена многократно для всего множества значений варьируемых параметров. Эти значения определяются в точках пересечения диагоналей прямоугольных ячеек, на которые разбивается плоскость этих параметров.

T₁

Затем для каждого сочетания значений параметров применяется критерий Рауса и находится число правых корней характеристического уравнения. Оно проставляется в виде цифры в соответствующей ячейке (вместо нуля обычно ставят точку, область устойчивости будет выделена этими точками как показано на рисунке).

§50. Структурная устойчивость

Система называется структурно-устойчивой, если ее можно сделать устойчивой без изменения структуры при некоторых положительных вещественных значениях ее параметров. Изменение структуры предполагает добавление или изъятие некоторых звеньев. На практике важно избегать структурно-неустойчивых вариантов и для этого применяются следующие условия структурной устойчивости одноконтурных систем:

1) Для системы без воздействия по первой производной, т.е. такой, у которой числитель передаточной функции в разомкнутом состоянии представляет собой лишь вещественный коэффициент k, т.е. , условие сводится к выполнению совместно двух неравенств

где q - число интегрирующих звеньев,

r - число неустойчивых звеньев первого порядка;

m - число консервативных звеньев;

n - порядок уравнения.

2) Для систем с воздействием по первой производной от рассогласования, т.е. при , условие сводится к выполнению совместно двух неравенств

Сравнение показывает, что воздействие по первой производной благоприятно влияет на устойчивость, т.к. неравенства для второго случая менее жесткие.

Пример. .

Здесь q = 2, n = 3, m = r = 0.

1. Считаем, что Т=0, тогда согласно условию 1 система структурно - неустойчива.

Это подтверждается характеристическим уравнением , для которого, как видно, нарушается необходимое условие устойчивости (нуль перед s).

2. Считаем, что Т>0, тогда согласно условию 2 система структурно - устойчива, что подтверждает и критерий Гурвица:

, т.е. при система будет устойчива, значит она структурно - устойчива.