§43. Анализ устойчивости систем с запаздыванием

Такая система содержит по крайней мере одно запаздывающее звено, и ей соответствует следующая структурная схема.

Передаточная функция РСАР:

, (1)

где - п. ф. предельной системы, т.е. САР без запаздывания.

Характеристическое уравнение ЗСАР 1+W_(s) = 0, или 1+W0(s)  e^-s = 0.

Это уравнение трансцедентное, т. к. содержит показательную функцию. Поэтому неприменимы критерии, предполагающие степенной вид характеристического полинома: алгебраические критерии, критерий Михайлова. Применим критерий Найквиста сначала к системе без запаздывания. Для этого построим АФХ W₀ (j) в предположении, что предельная система в замкнутом состоянии устойчива, найдем частоту среза и запас по фазе  (кривая 1).

Проанализируем, как в соответствии с формулой (1) деформируется АФХ

(2)

Формула (2) показывает, что при введении запаздывания каждый вектор афх предельной системы поворачивается на угол -  не меняя своей длины (т. к. W₀(j) остался прежним). Из-за этого АФХ приближается к опасной точке и может ее охватить, поэтому устойчивость снижается. Рассмотрим случай колебательной границы устойчивости, т. е. когда W_ (j_c) = -1 при =_гр.

Это может произойти если W₀ (j_c) повернуть на угол  по часовой стрелке. С другой стороны, этот угол поворота равен ω_сτ_гр. Отсюда получаем формулу для расчета граничного запаздывания:

. (3)

В простейших случаях ЗСАР устойчива при  < _гр и наоборот. В сложных случаях возможно несколько граничных значений запаздывания, когда W₀ (j) пересекает окружность единичного радиуса несколько раз (кривая 2). Если эти граничные значения, найденные по формуле (3), отложить на числовой оси, то получим разбивку оси на области устойчивости и неустойчивости.

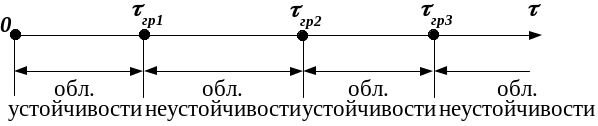
§44. Устойчивость сар с иррациональными передаточными функциями

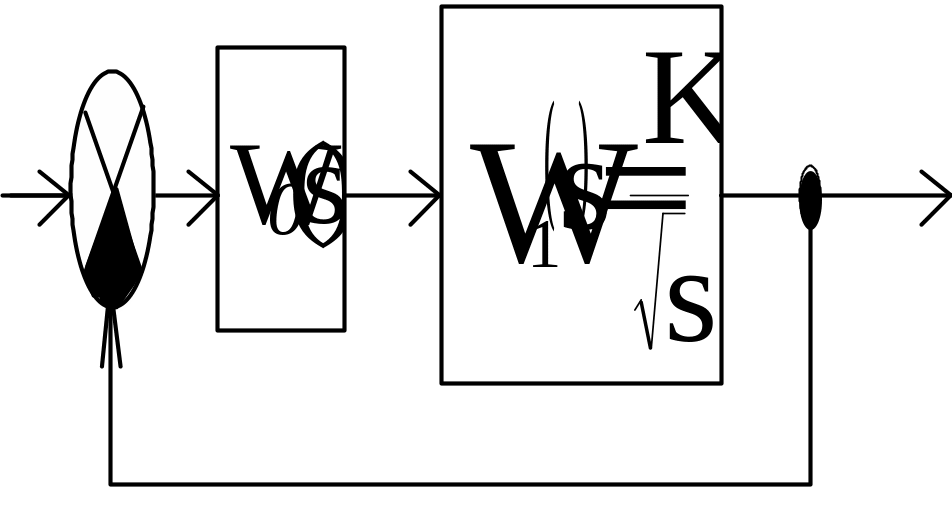
Такие случаи возникают в системе, имеющей особые звенья с распределенными параметрами, описываемые уравнением теплопроводности.

Передаточная функция РСАР . Характеристическое уравнение ЗСАР:

или . (1)

Характеристическое уравнение, как и п. ф. иррационально. Эта особенность не позволяет применить алгебраические критерии устойчивости несмотря на то, что с помощью замены переменной п. ф. и характеристическое уравнение можно привести к рациональному виду. Но при этом граница области устойчивости в плоскости корней переменной q видоизменяется. На плоскости s граница устойчивости, как известно, имеет уравнение , а соответственно для плоскости q её уравнение . Данная формула показывает, что в плоскости q границей области устойчивости являются лучи, проведенные из начала координат под углом к вещественной оси.

Для анализа возможности применения частотных критериев выведем принцип аргумента для переменной q. Предполагаем, что сделано разложение .

Определяем графически углы поворота векторов, образованных левыми и правыми корнями q_i при q= :

(2)

Если характеристическое уравнение (1), записанное после замены переменных в виде A(q)=0, имеет m - правых и (n - m) - левых корней, то принцип аргумента выразится формулой в соответствии с (2):

.

Отсюда можно сформулировать критерий Михайлова для этих ЗСАР:

ЗСАР устойчива (m = 0), если кривая Михайлова в виде годографа при изменении =0 до  обходит последовательно n/2 квадрантов, где n - порядок характеристического уравнения для переменной q.

Если учесть, что для переменной s порядок n/2, то по существу критерий Михайлова сохраняет свою основную формулировку, и для его применения замены делать не нужно. Проанализировав изменение аргумента вектора

, получим формулу , что совпадает с известной формулой для рациональных п. ф.(см. §8). Следо-вательно критерий Найквиста, основанный на этой формуле, применим без всяких изменений к данным системам.

Пример. Определить с помощью критерия Найквиста граничное значение коэффициента К для системы с иррациональной п. ф. полу интегрирующего звена. Запишем известное условие колебательной границы устойчивости по критерию Найквиста, т.е. условие прохождения АФХ через опасную точку при частоте _:

.

Вместо этого можно записать 2 уравнения (для модулей и аргументов):

Отсюда вытекает следующий порядок расчета:

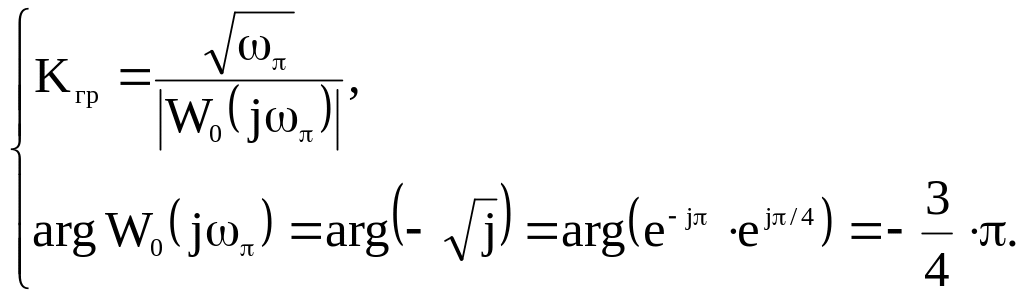
1) необходимо построить АФХ W₀( j);

2) на этой характеристике следует найти точку, соответствующую частоте _ РСАР, проведя луч под углом –0,75π;

3) найти К_гр из первого уравнения системы.