
- •§1. Комплексные числа и действия над ними
- •1.Понятие комплексного числа. Действия над комплексными числами
- •2. Геометрическая интерпретация комплексного числа.
- •3. Комплексная плоскость как метрическое пространство
- •§2.Последовательности комплексных чисел. Предел последовательности
- •§3. Расширенная комплексная плоскость
- •§4. Функции комплексного переменного
- •1. Комплексно-значные функции действительной переменной
- •2. Кривые на комплексной плоскости
- •3.Функции комплексного переменного
- •§5. Предел и непрерывность функции комплексного переменного
- •1. Предел функции комплексного переменного
- •2.Непрерывность функции комплексного переменного
- •§6. Геометрическая интерпретация функции комплексного переменного
- •§7.Дифференцирование функции одной комплексной переменной
- •1.Производная функции комплексной переменной
- •2. Необходимые и достаточные условия
- •3. Понятие аналитической функции
- •4. Гармонические функции
- •5. Восстановление аналитической функции
- •6. Геометрический смысл аргумента и модуля производной
- •7. Понятие о конформном отображении
- •§8. Простейшие элементарные функции комплексной переменной
- •1. Линейная функция
- •2. Дробно-линейная функция
- •3.Многочлен
- •4. Показательная функция
- •5. Тригонометрические функции
- •6. Гиперболические функции
- •7. Области однолистности аналитических функций. Обратные функции
- •8. Степенная функция и радикал
- •9. Логарифмическая функция
- •10. Общие степенная и показательная функции
- •§9. Интегрирование функций комплексного переменного
- •1.Понятие интеграла
- •2.Вычисление интеграла от функции комплексного переменного
- •3.Основные свойства интеграла от функции комплексного переменного
- •§10. Интегральная теорема Коши
- •§11. Первообразная
- •§12. Интегральная формула Коши и ее следствия
- •1. Интегральная формула Коши
- •2. Бесконечная дифференцируемость аналитической функции
- •3. Теорема Морера
- •4. Теорема о среднем
- •5. Принцип максимума модуля аналитической функции
3. Понятие аналитической функции
Определение.
Функция f(z)
называется аналитической
(голоморфной,
регулярной,
правильной)
в точке
![]() ,
если она дифференцируема в каждой точке
некоторой окрестности точки
.
,
если она дифференцируема в каждой точке
некоторой окрестности точки
.
Заметим, что необходимо различать понятие дифференцируемости в точке и понятие аналитичности в точке:
f(z)
дифференцируема в точке
![]() ,
,
f(z)
аналитическая в точке
![]()
Определение. Функция f(z) называется аналитической в области G, если она дифференцируема в каждой точке этой области. Т.е. понятия дифференцируемости и аналитичности в области совпадают.
Примеры.
1)
![]() - аналитическая на
.
- аналитическая на
.
2)
![]() аналитическая
на
.
аналитическая
на
.
3)
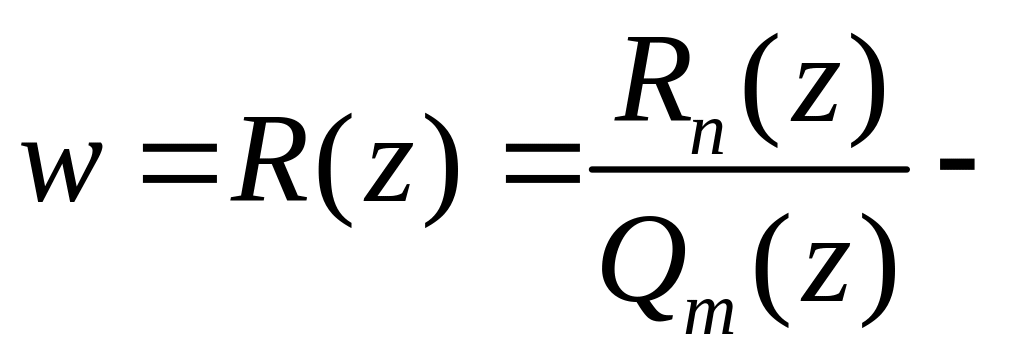 аналитическая
на
аналитическая
на
![]() .
.
4)
![]() нигде
не является аналитической, так производная
существует только в точке
(см. пример 2 п.2).
нигде
не является аналитической, так производная
существует только в точке
(см. пример 2 п.2).
4. Гармонические функции
Определение.
Дифференциальное уравнение с частными
производными второго порядка
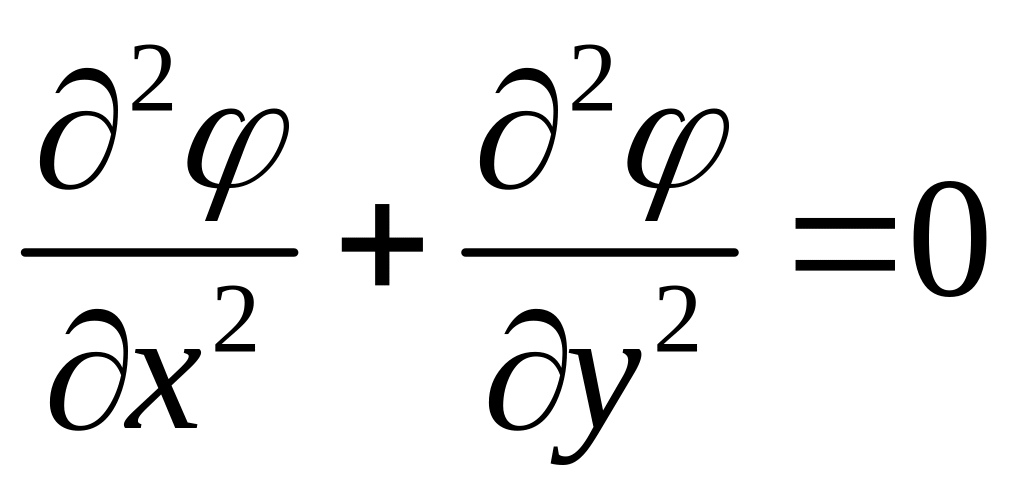 называется уравнением
Лапласа.
называется уравнением
Лапласа.
Обозначим
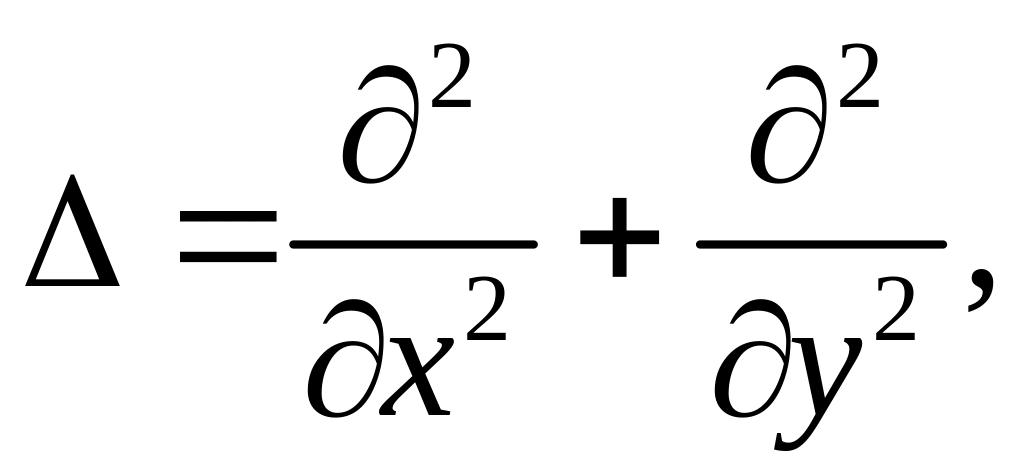 тогда
тогда
![]() -краткая
запись уравнения Лапласа.
-краткая
запись уравнения Лапласа.
Определение. Действительная функция двух действительных переменных называется гармонической на области G, если она имеет непрерывные частные производные второго порядка и на G удовлетворяет уравнению Лапласа.
Определение. Две гармонические функции, связанные условиями Коши – Римана, называются сопряжёнными гармоническими функциями.
Позже будет доказано, что производная аналитической функции сама является аналитической функцией. Используем этот факт при доказательстве следующей теоремы.
Теорема 5. Для того чтобы функция f(z)=u(x,y)+iv(x,y) была аналитической в области G необходимо и достаточно, чтобы её действительная и мнимая часть были сопряжёнными гармоническими функциями.
Доказательство.
1) Пусть f(z)=u(x,y)+iv(x,y) аналитическая в некоторой области G. Тогда по теореме 2 u(x,y) и v(x,y)-дифференцируемые функции двух действительных переменных и удовлетворяют условиям Коши – Римана:
.
Производная может быть представлена в одном из видов:
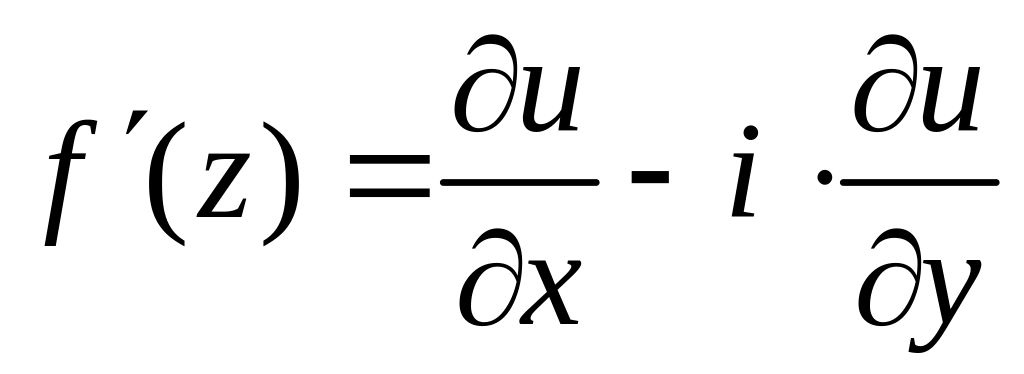 или
или
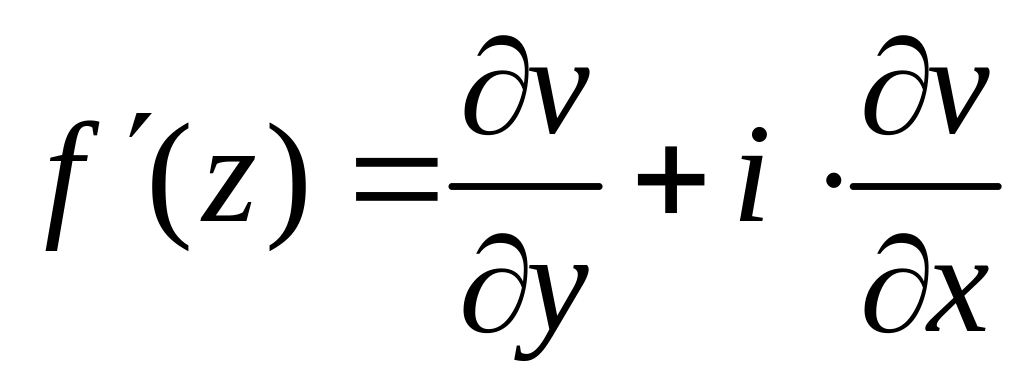 .
.
Так как
производная аналитической функции
является аналитической функцией, то
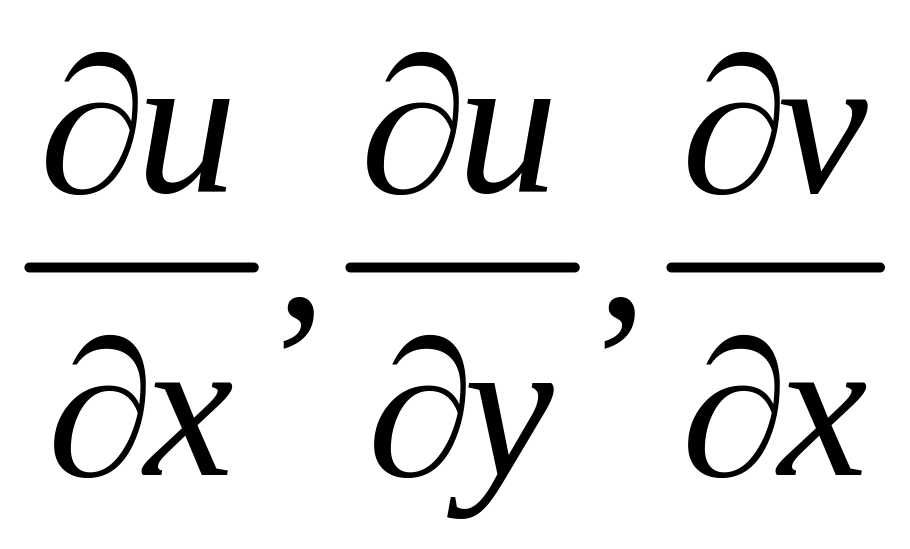 и
и
![]() тоже дифференцируемые функции двух
действительных переменных и удовлетворяют
условиям Коши – Римана.
тоже дифференцируемые функции двух
действительных переменных и удовлетворяют
условиям Коши – Римана.
Применим
к паре функций
![]() и
и
![]() первое условие Коши– Римана, а для
функций
и
первое условие Коши– Римана, а для
функций
и
![]() - второе:
- второе:
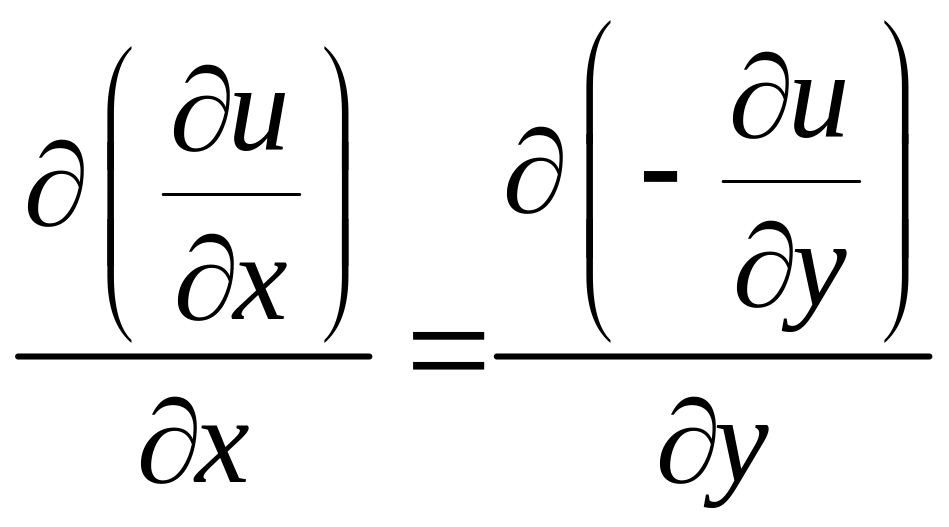 ,
, 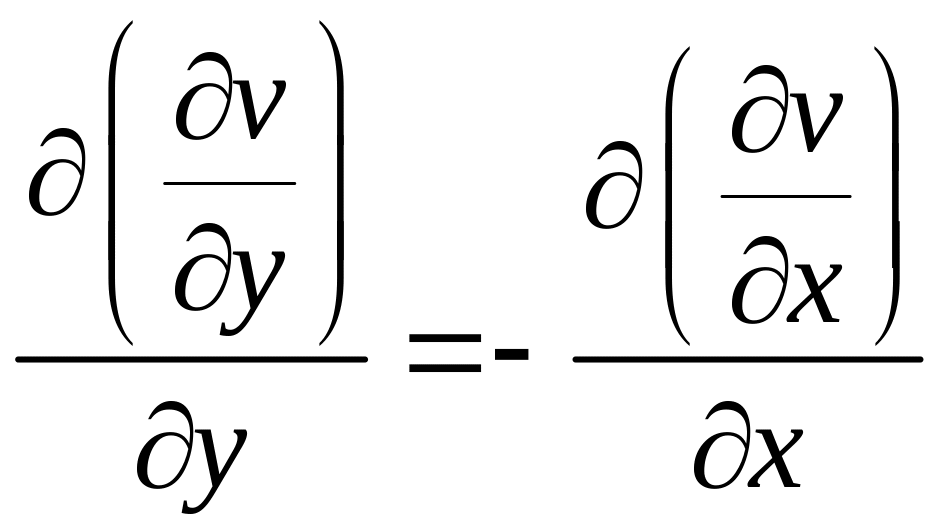 ,
,
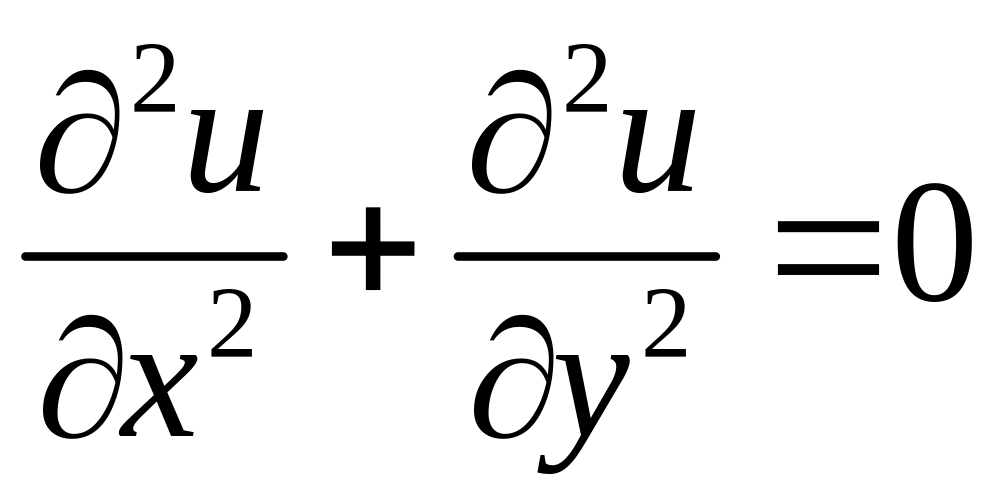 , (7)
, (7) 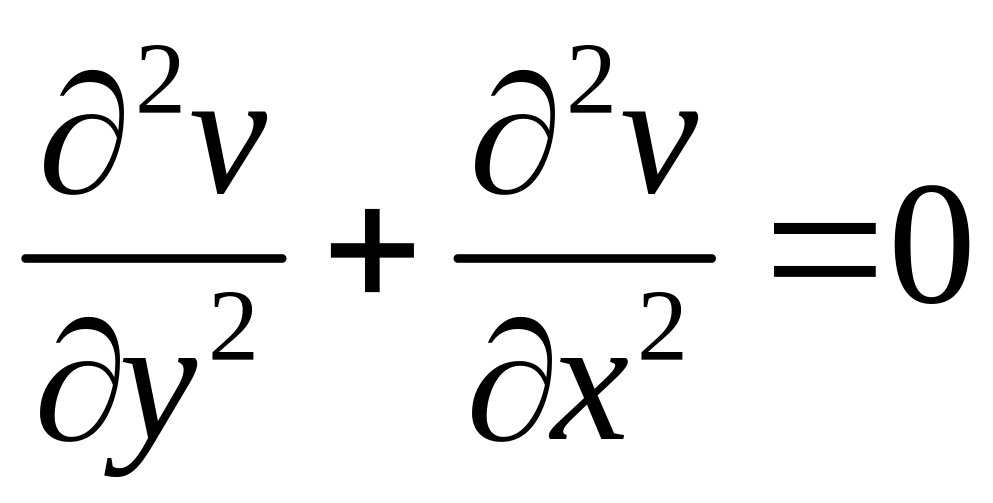 , (8)
, (8)
т.е. u и v удовлетворяют уравнению Лапласа.
Покажем,
что u(x,y)
и v(x,y)
имеют непрерывные частные производные
второго порядка. Т.к. f(z)
- аналитическая функция, то
![]() -тоже
аналитическая функция.
-тоже
аналитическая функция.
Дифференцируя
![]() по x,
получим
по x,
получим
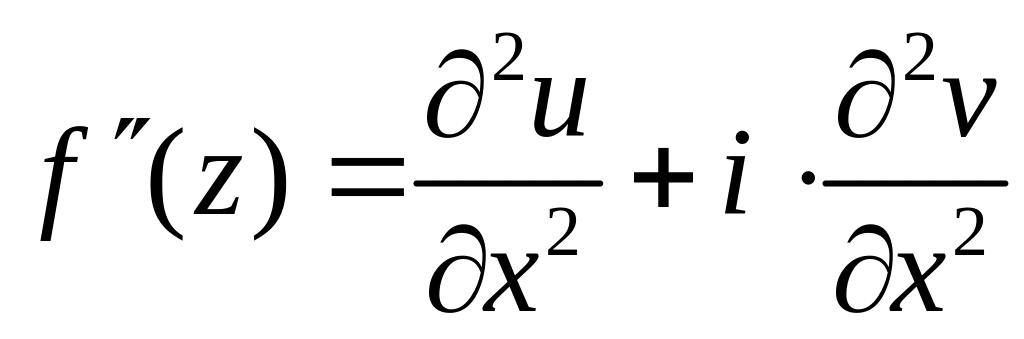 .
.
Из
(7), (8)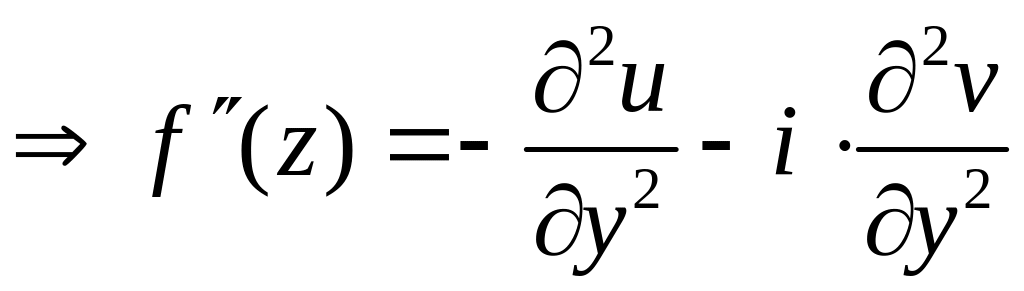 .
.
Дифференцируя
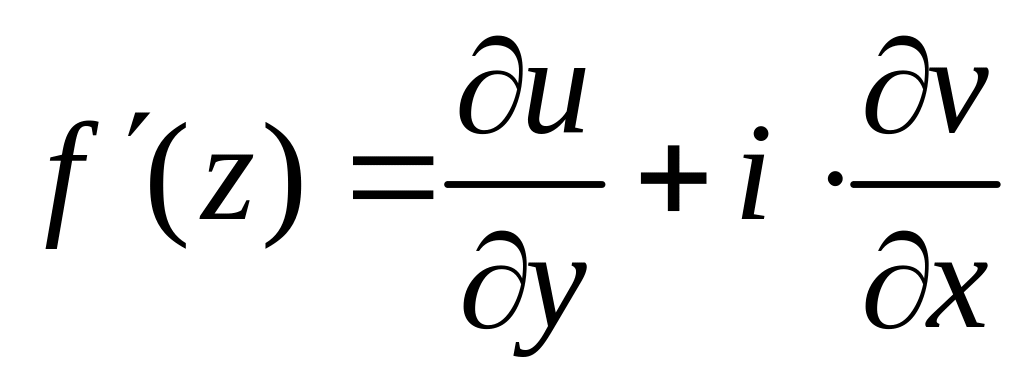 по y,
получим
по y,
получим
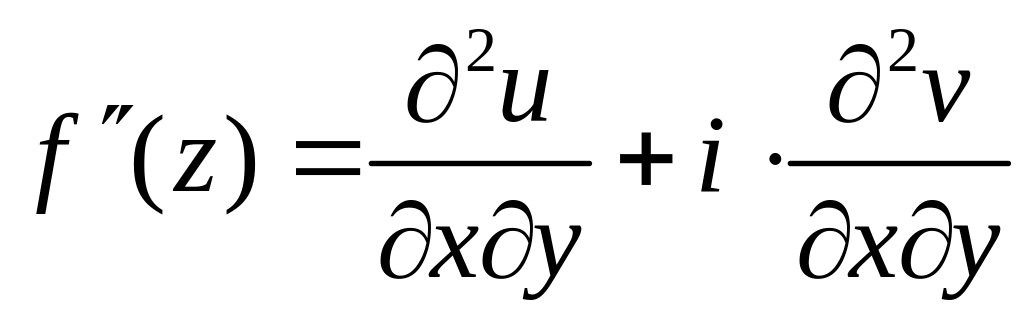 ,
,
т.е.
![]() является аналитической функцией и
может быть представлена в одном из
видов:
является аналитической функцией и
может быть представлена в одном из
видов:
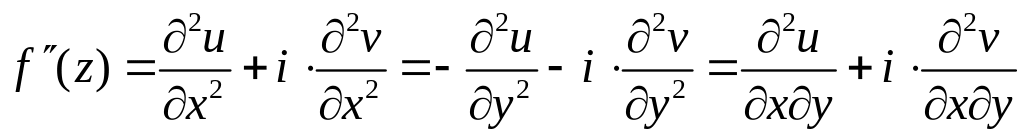 .
.
Значит, все частные производные второго порядка являются (по теореме 2) дифференцируемыми в области G функциями, следовательно, они непрерывны.
Итак, u(x,y) и v(x,y) имеют в G непрерывные частные производные второго порядка, удовлетворяют уравнению Лапласа и условиям Коши – Римана. Значит, они являются сопряжёнными гармоническими функциями.
2.
![]() Пусть
u(x,y)
и v(x,y)
какие – либо сопряжённые гармонические
в области G
функции. Так как они дифференцируемы
и удовлетворяют условиям Коши – Римана,
то по теореме 2 функция f(z)=u(x,y)+iv(x,y)
является дифференцируемой в G
и, следовательно, она аналитическая в
G.
.
Пусть
u(x,y)
и v(x,y)
какие – либо сопряжённые гармонические
в области G
функции. Так как они дифференцируемы
и удовлетворяют условиям Коши – Римана,
то по теореме 2 функция f(z)=u(x,y)+iv(x,y)
является дифференцируемой в G
и, следовательно, она аналитическая в
G.
.
Из теоремы 5 следует, что действительной или мнимой частью аналитической функции может быть только гармоническая функция.
Например,
не существует аналитической функции
f(z),
у которой
![]() Действительно,
функция
Действительно,
функция
![]() не является гармонической ни в какой
области G.
не является гармонической ни в какой
области G.
![]() ,
, 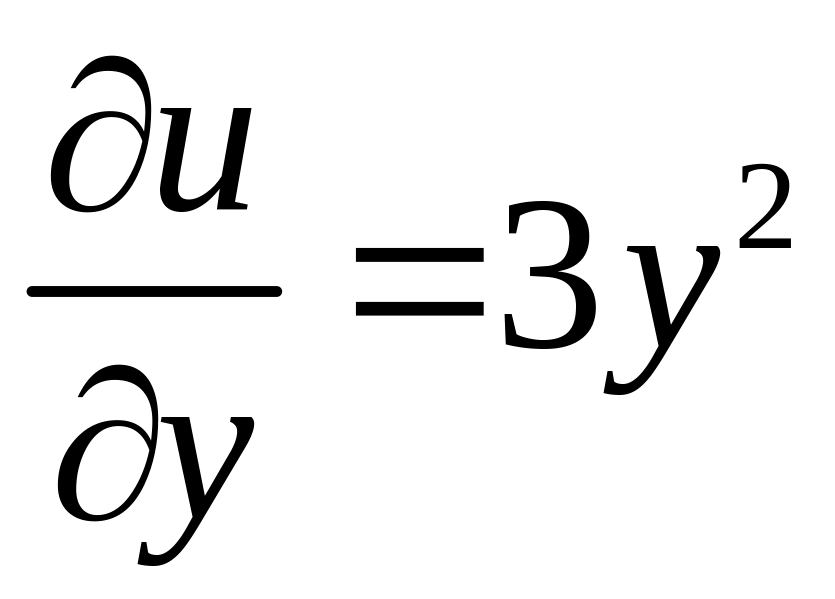 ,
, 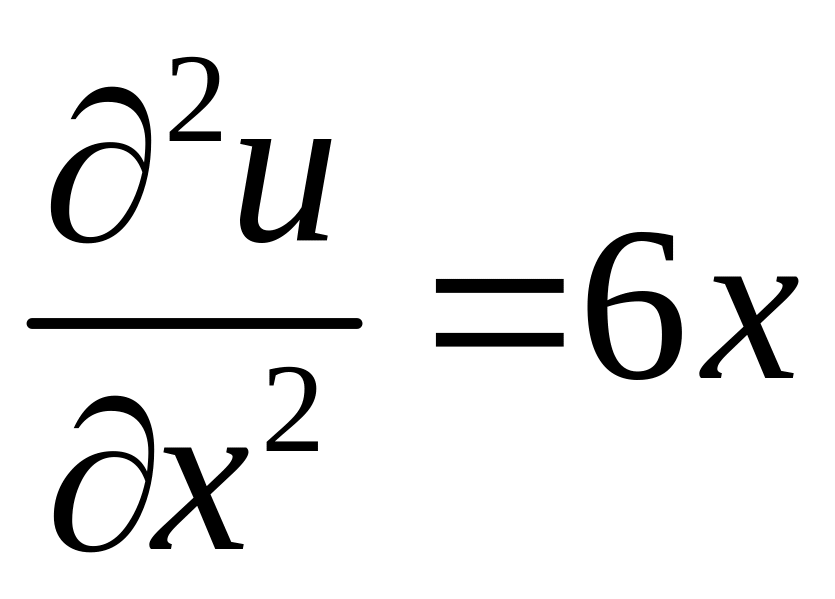 ,
, 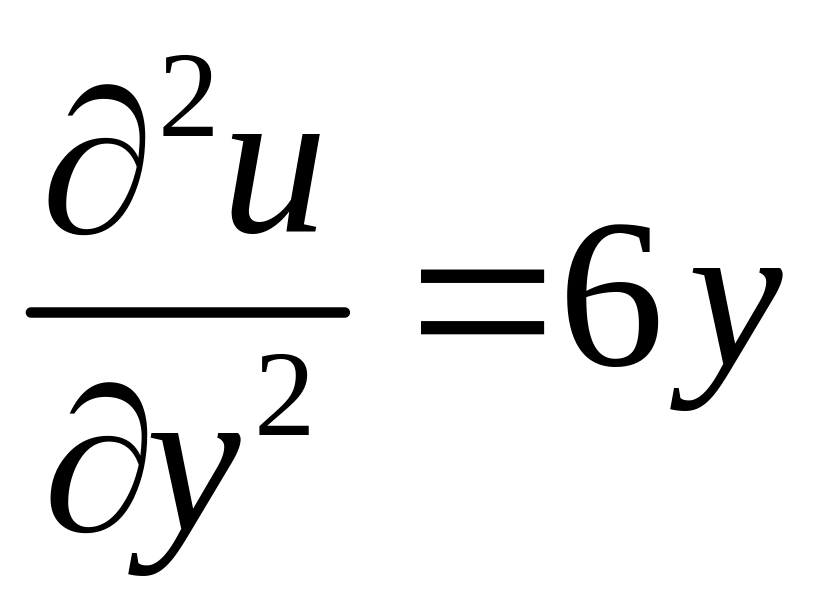 .
.
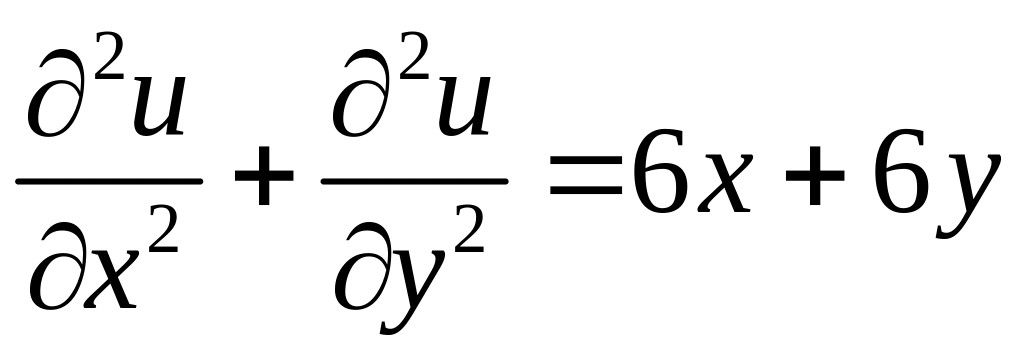 .
Следовательно,
.
Следовательно,
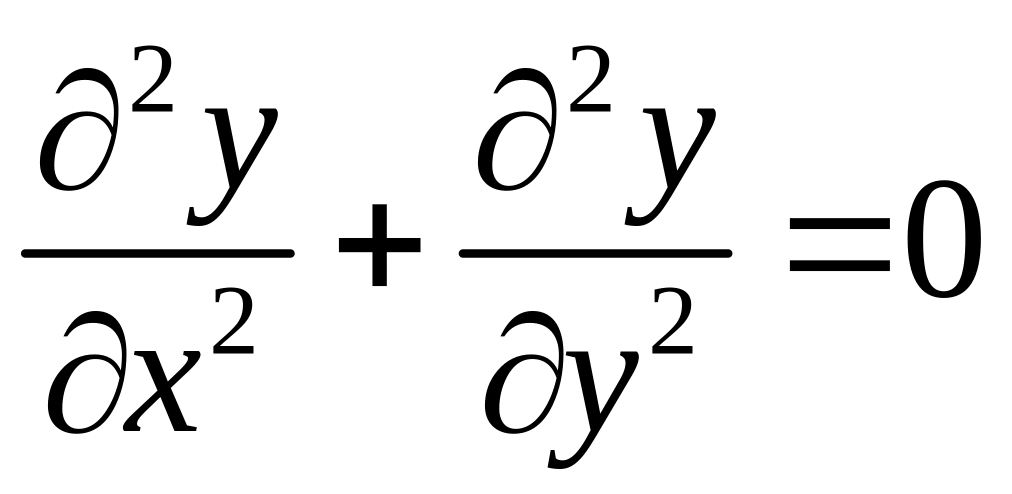 только
на прямой
только
на прямой
![]() (не
является областью). Значит, u(x,y)
не является гармонической ни в какой
области G
из
.
(не
является областью). Значит, u(x,y)
не является гармонической ни в какой
области G
из
.
