
- •§1. Комплексные числа и действия над ними
- •1.Понятие комплексного числа. Действия над комплексными числами
- •2. Геометрическая интерпретация комплексного числа.
- •3. Комплексная плоскость как метрическое пространство
- •§2.Последовательности комплексных чисел. Предел последовательности
- •§3. Расширенная комплексная плоскость
- •§4. Функции комплексного переменного
- •1. Комплексно-значные функции действительной переменной
- •2. Кривые на комплексной плоскости
- •3.Функции комплексного переменного
- •§5. Предел и непрерывность функции комплексного переменного
- •1. Предел функции комплексного переменного
- •2.Непрерывность функции комплексного переменного
- •§6. Геометрическая интерпретация функции комплексного переменного
- •§7.Дифференцирование функции одной комплексной переменной
- •1.Производная функции комплексной переменной
- •2. Необходимые и достаточные условия
- •3. Понятие аналитической функции
- •4. Гармонические функции
- •5. Восстановление аналитической функции
- •6. Геометрический смысл аргумента и модуля производной
- •7. Понятие о конформном отображении
- •§8. Простейшие элементарные функции комплексной переменной
- •1. Линейная функция
- •2. Дробно-линейная функция
- •3.Многочлен
- •4. Показательная функция
- •5. Тригонометрические функции
- •6. Гиперболические функции
- •7. Области однолистности аналитических функций. Обратные функции
- •8. Степенная функция и радикал
- •9. Логарифмическая функция
- •10. Общие степенная и показательная функции
- •§9. Интегрирование функций комплексного переменного
- •1.Понятие интеграла
- •2.Вычисление интеграла от функции комплексного переменного
- •3.Основные свойства интеграла от функции комплексного переменного
- •§10. Интегральная теорема Коши
- •§11. Первообразная
- •§12. Интегральная формула Коши и ее следствия
- •1. Интегральная формула Коши
- •2. Бесконечная дифференцируемость аналитической функции
- •3. Теорема Морера
- •4. Теорема о среднем
- •5. Принцип максимума модуля аналитической функции
2. Необходимые и достаточные условия
дифференцируемости функции комплексной переменной
Теорема
3. Пусть
функция
![]() определена в некоторой области G.
Для того, чтобы функция f(z)
была дифференцируемой в точке z
области G
необходимо и достаточно, чтобы
определена в некоторой области G.
Для того, чтобы функция f(z)
была дифференцируемой в точке z
области G
необходимо и достаточно, чтобы
функции u(x;y) и v(x;y) были дифференцируемы в точке z как функции двух действительных переменных;
в точке z выполнялись равенства
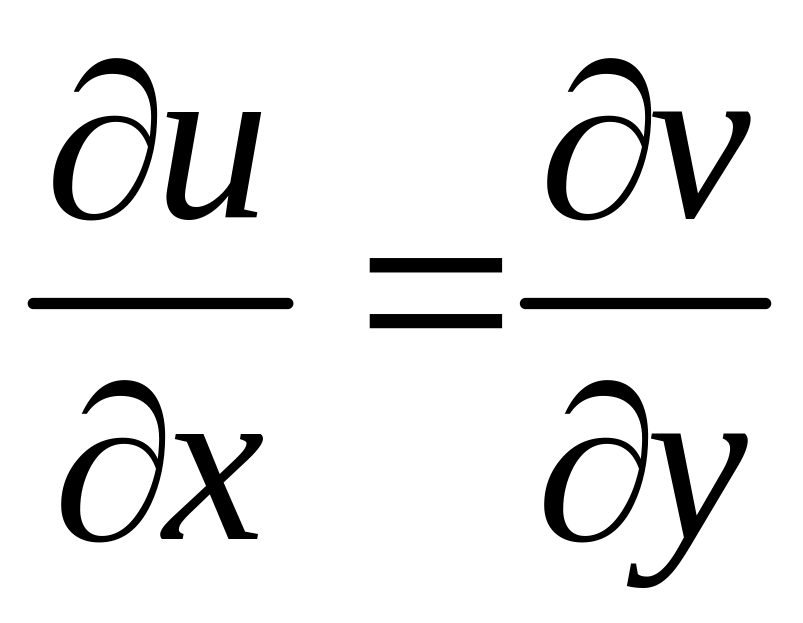 и
и
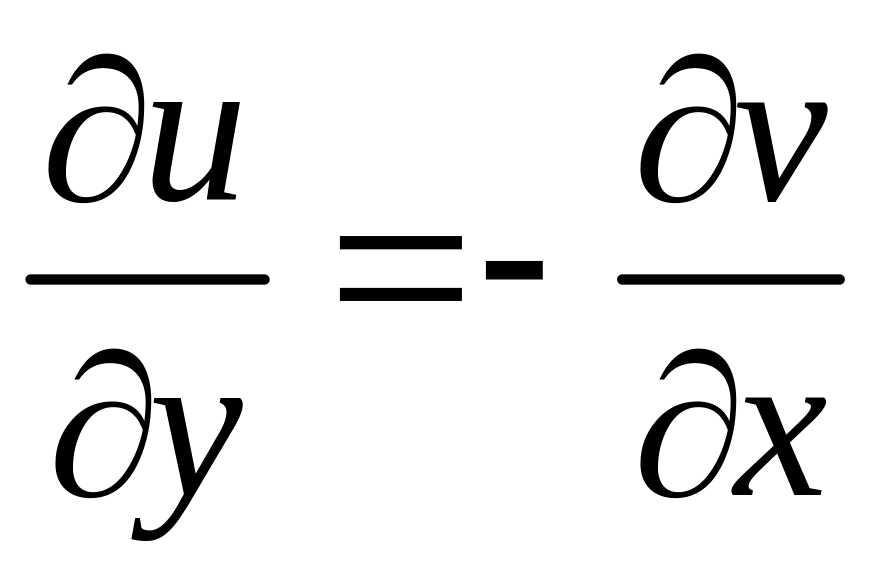 . (1)
. (1)
При выполнении всех условий теоремы производная может быть представлена в одном из следующих видов:
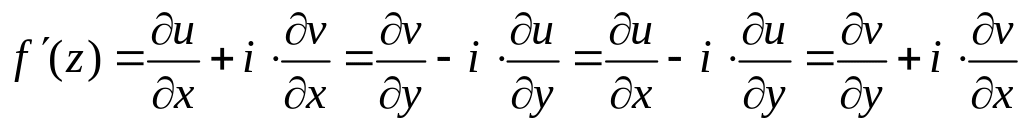 . (2)
. (2)
Равенства (1) называются условиями Коши-Римана (или Даламбера-Эйлера).
Доказательство.
1) Необходимость.
Пусть функция f(z) дифференцируема в точке z области G. Тогда по теореме 1 ее приращение может быть представлено в виде
![]() ,
где
.
,
где
.
-
комплексная функция от z.
Следовательно,
![]() ,
где
,
где
![]() .
- комплексное
число, значит,
.
- комплексное
число, значит,
![]() ,
a,b
.
Тогда
,
a,b
.
Тогда
f(z)=u+iv=(a+ib)(x+iy)+(1+i2)(x+iy)=ax-by+i(ay+bx)+
+1x-2y+i(1y+2x)=(ax-by+1x-2y)+i(ay+bx+1y+2x).
Отсюда
u=ax-by+1x-2y,
v=bx+ay+2x+1y, где . (3)
Из (3) следует, что
1) функции u(x;y) и v(x;y) дифференцируемы в точке (x;y),
2) их частные производные в точке (x;y):
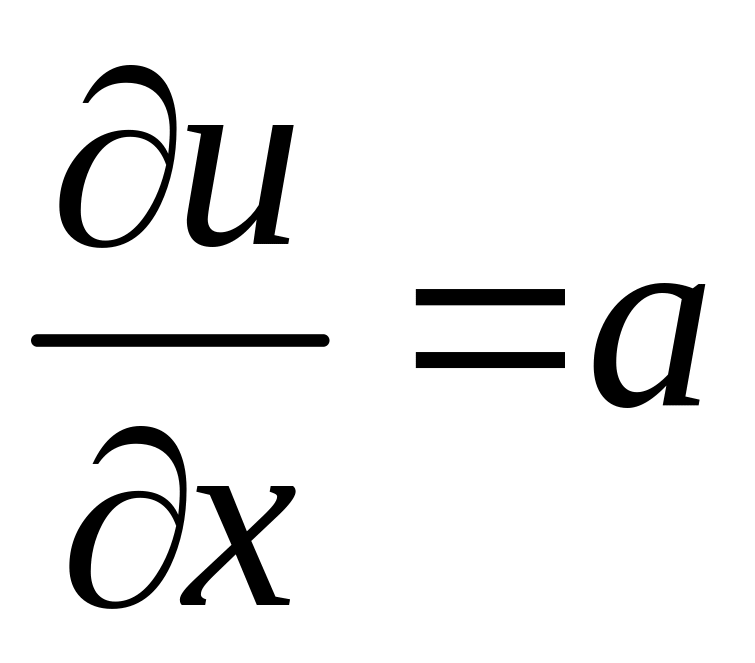 ,
,
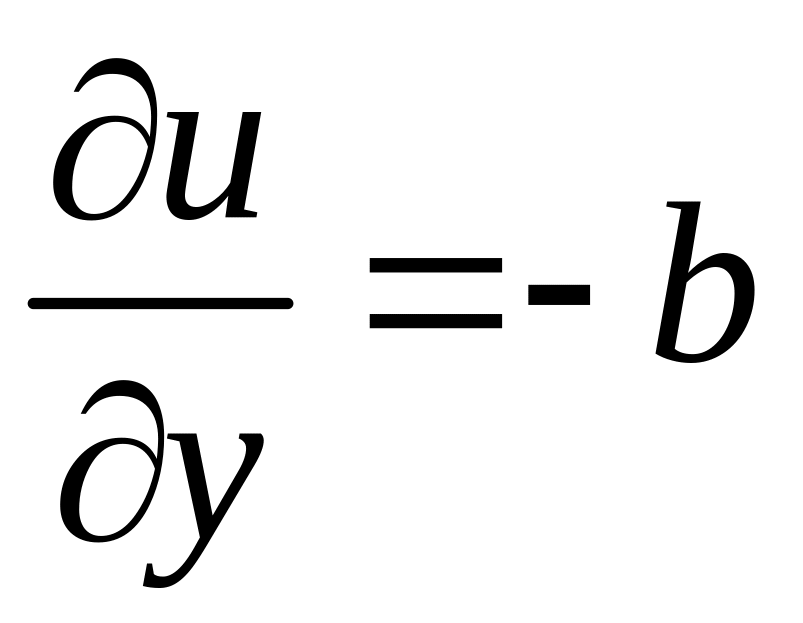 ,
,
![]() ,
,
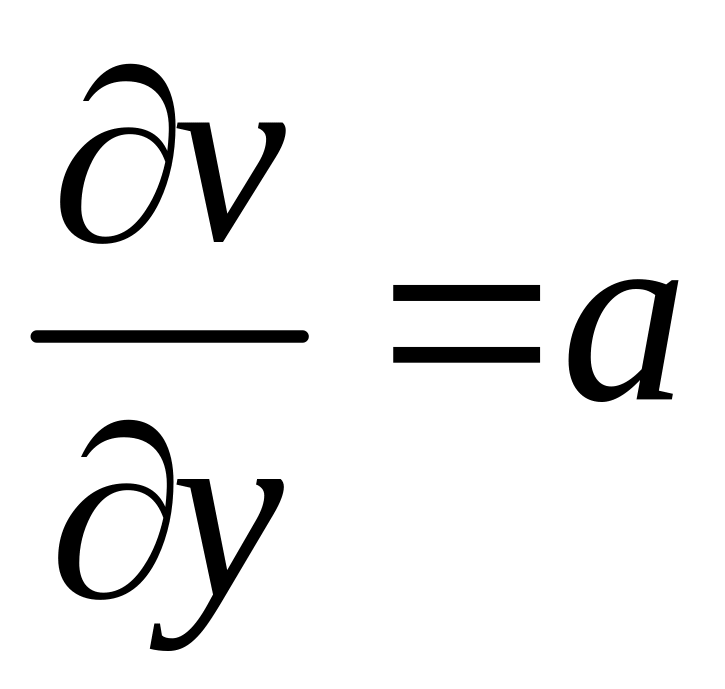 .
.
Отсюда , , т.е. удовлетворяют условиям Коши-Римана.
Тогда для производной получаем:
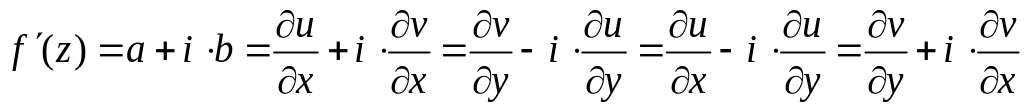 .
.
2) Достаточность.
Пусть в точке z области G выполнены условия 1) и 2) теоремы. Придадим точке z=(x;y) приращение z=x+iy0. По условию
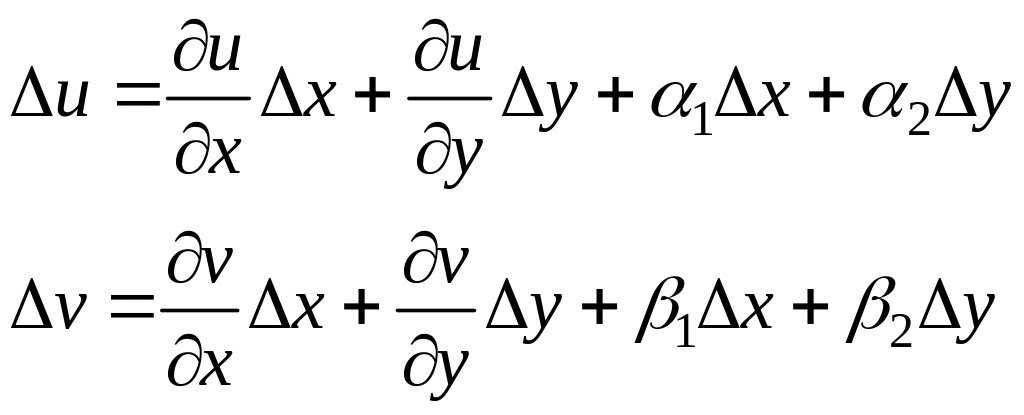 где
где
![]() . (4)
. (4)
Приращение
функции
![]() ,
соответствующее приращению
,
соответствующее приращению
![]() ,
имеет вид:
,
имеет вид:
![]() .
Разделим на
:
.
Разделим на
:
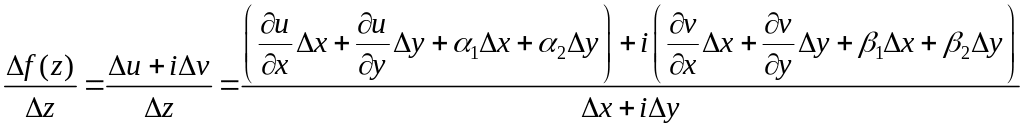 .
Используя условия Коши-Римана, перейдём
к частным производным по x:
.
Используя условия Коши-Римана, перейдём
к частным производным по x:
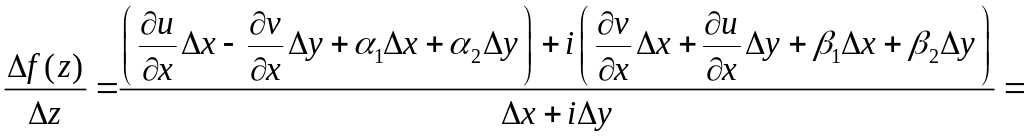
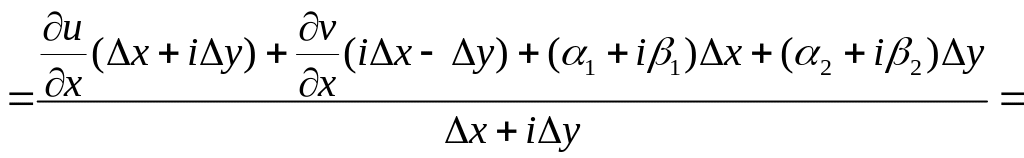
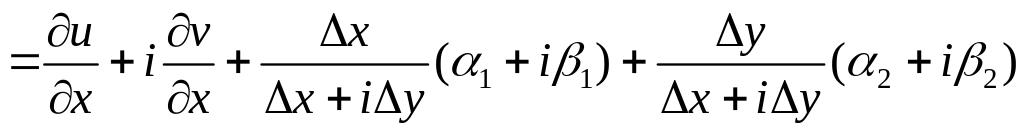 . (5)
. (5)
Т.к.
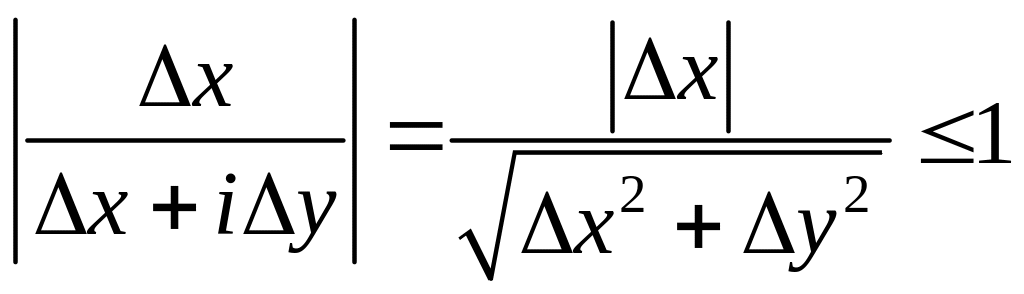 ,
,
 ,
и
,
и
![]() ,
то
,
то
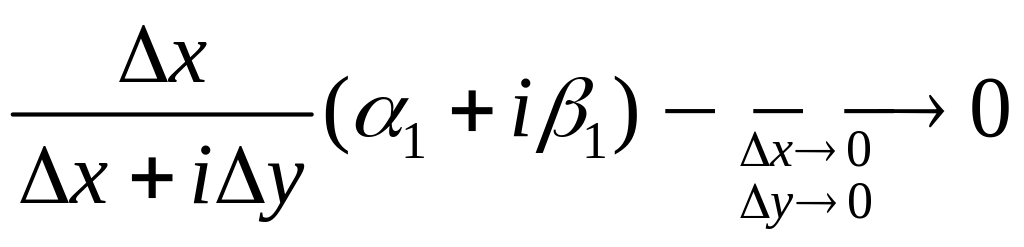 и
и
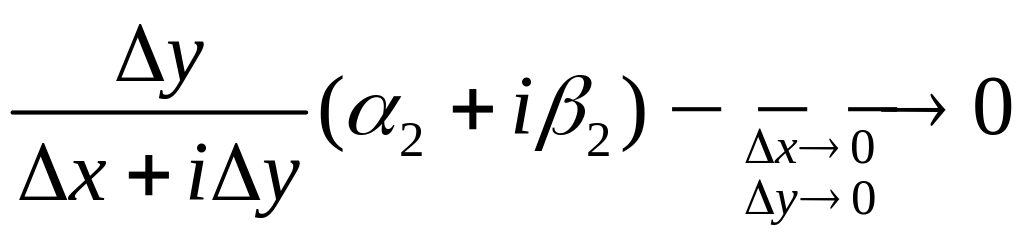 (огр.БМФ).
(огр.БМФ).
Следовательно,
переходя в (5) к
![]() ,
получим:
,
получим:
![]() ,
т.е. f(z)
дифференцируема в точке z.
,
т.е. f(z)
дифференцируема в точке z.
Формулами (2) можно пользоваться для вычисления производных.
Пример
1.
f(z)=![]() .
.
u(x,y)=![]() ,
v(x,y)=2xy
- дифференцируемы на
.
,
v(x,y)=2xy
- дифференцируемы на
.![]()
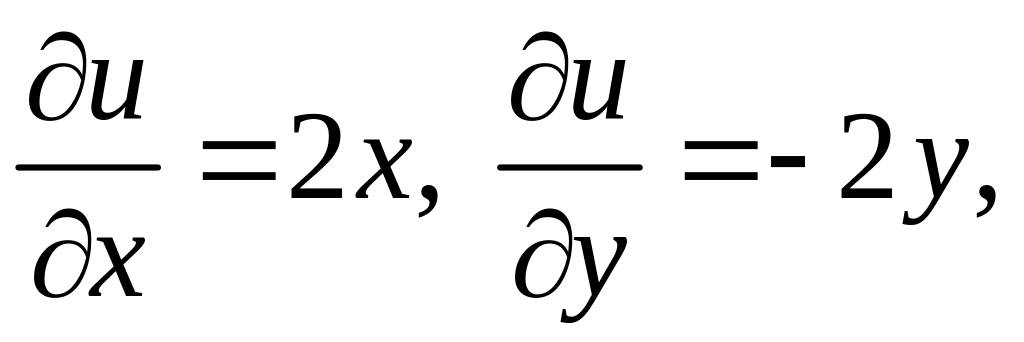
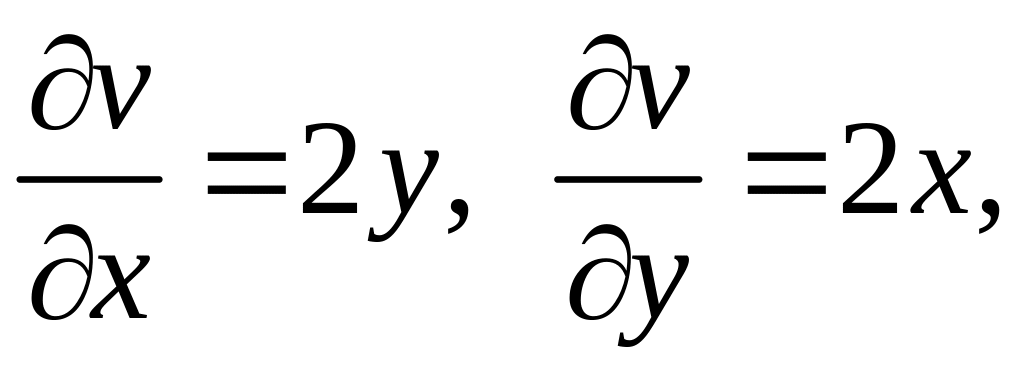 ,
,
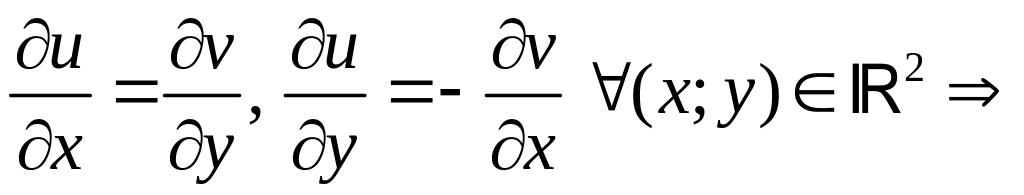 условия
Коши-Римана выполнены на
.
условия
Коши-Римана выполнены на
.
Значит,
функция
![]() дифференцируема
на
и
дифференцируема
на
и
![]() .
.
Замечание. Если функция задана в виде w=f(z) и её дифференцируемость можно установить, пользуясь основными правилами дифференцирования, то нет необходимости использовать теорему 3.
Пример2.
Доказать, что функция
![]() дифференцируема только в точке
дифференцируема только в точке
![]() и найти
и найти
![]()
![]()
![]() -
дифференцируемы в любой точке
.
-
дифференцируемы в любой точке
.
Но
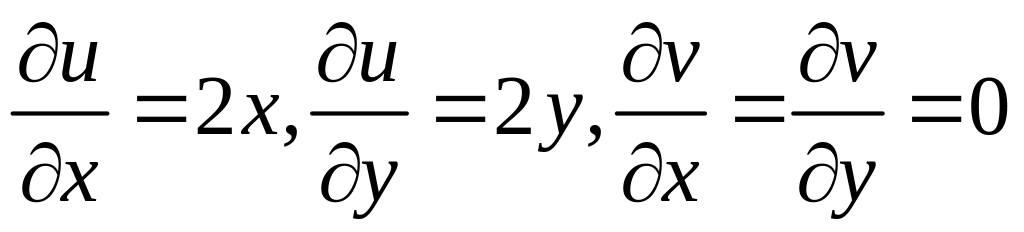 и, следовательно,
условия
Коши – Римана выполняются только в
точке z=0,
поэтому функция дифференцируема только
в этой точке и
и, следовательно,
условия
Коши – Римана выполняются только в
точке z=0,
поэтому функция дифференцируема только
в этой точке и
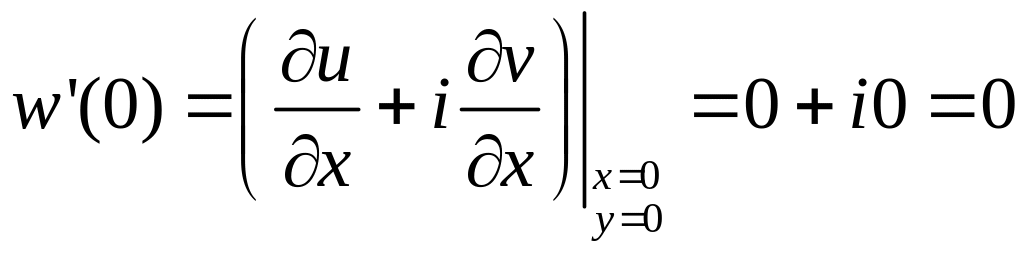 .
.
Часто используются условия дифференцируемости функций комплексного переменного, выраженные в полярных координатах r и .
Теорема
4.
Пусть функция
![]() определена в некоторой области G.
Для того чтобы функция f(z)
была дифференцируема в некоторой точке
определена в некоторой области G.
Для того чтобы функция f(z)
была дифференцируема в некоторой точке
![]() необходимо и достаточно, чтобы:
необходимо и достаточно, чтобы:
1) u и v являлись дифференцируемыми функциями от r и ,
2) их частные производные удовлетворяли соотношениям:
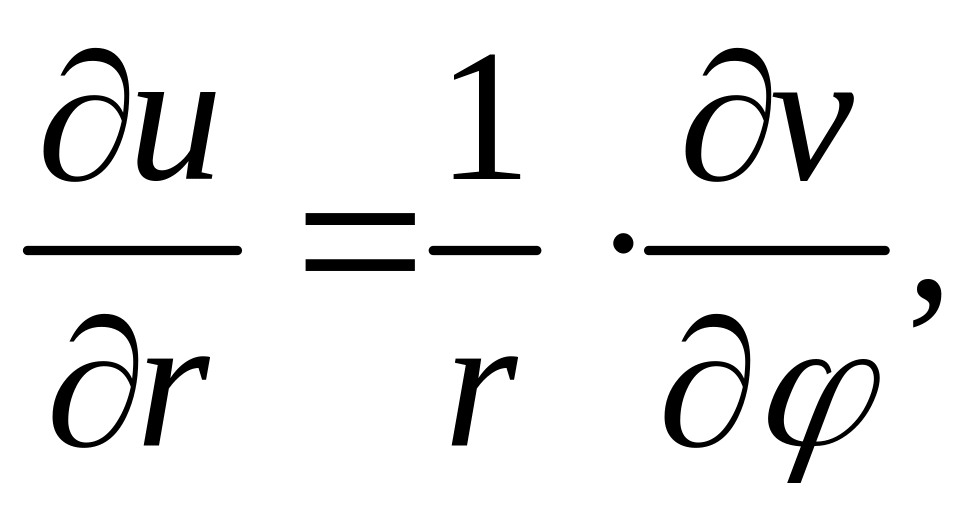
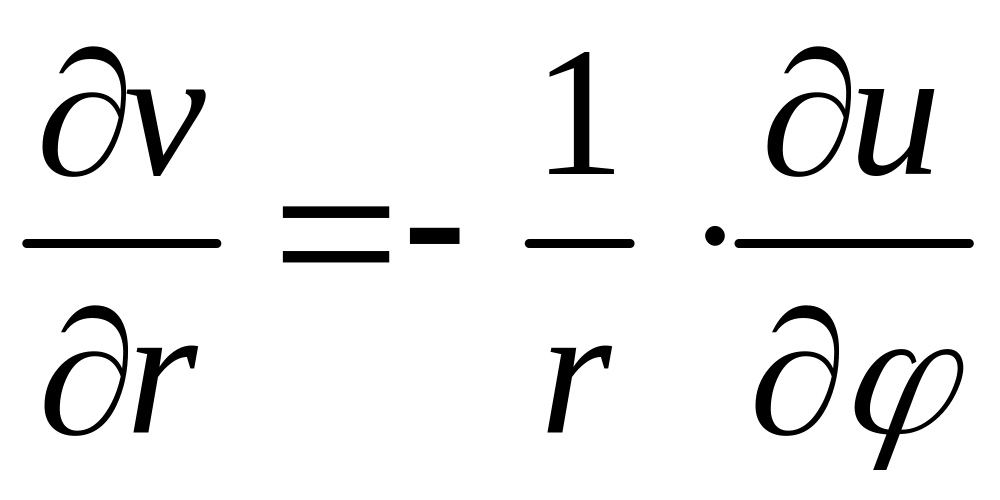 . (6)
. (6)
Доказательство.
1)![]() Пусть f(z)
дифференцируема
в точке
.
Так как f(z)=u(x,y)+iv(x,y),
u(x,y)
и v(x,y)
дифференцируемы как функции двух
переменных x
и y
(по теореме 3), а
Пусть f(z)
дифференцируема
в точке
.
Так как f(z)=u(x,y)+iv(x,y),
u(x,y)
и v(x,y)
дифференцируемы как функции двух
переменных x
и y
(по теореме 3), а
![]() дифференцируемы как функции двух
переменных r
и ,
то функции
дифференцируемы как функции двух
переменных r
и ,
то функции
![]() и
и
![]() дифференцируемы
как сложные функции от r
и .
дифференцируемы
как сложные функции от r
и .
Покажем теперь, что выполнены условия (6).
По правилу дифференцирования сложной функции двух переменных:
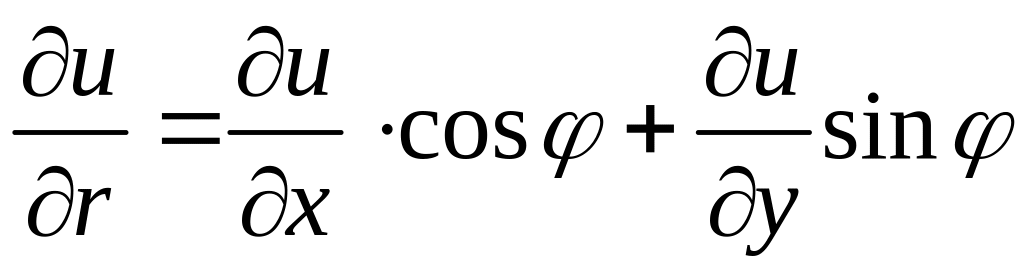 ,
,
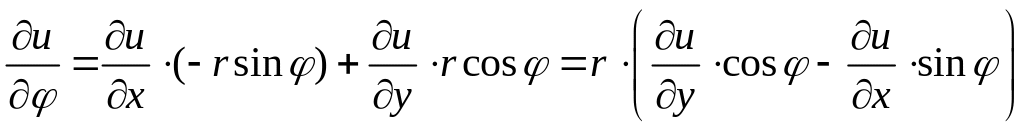
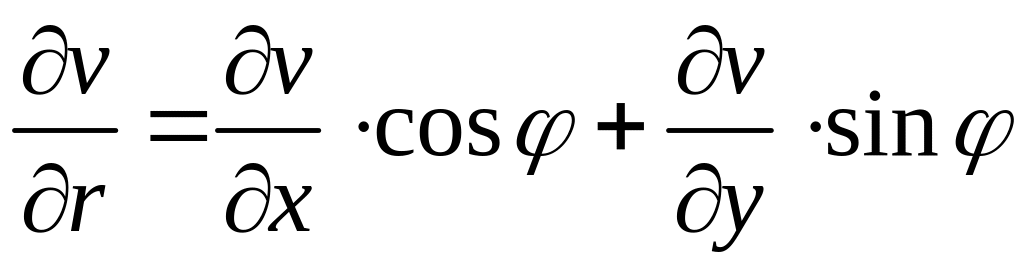 ,
,
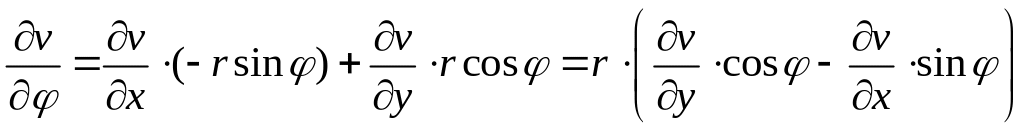 .
.
Используя условия (1), получим:
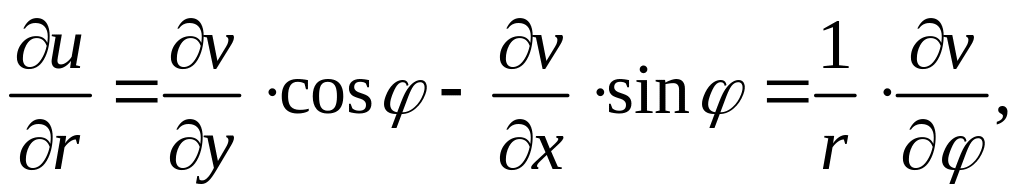
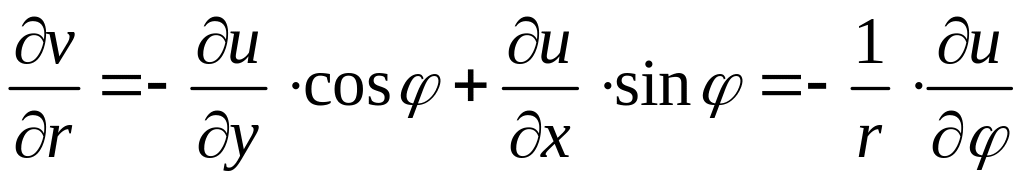 .
.
Следовательно, условия (6) выполнены.
2) (![]() )
Пусть функции
и
дифференцируемы
в точке
)
Пусть функции
и
дифференцируемы
в точке
![]() .
Тогда так как
.
Тогда так как
![]() и
и
![]() дифференцируемы в этой точке, то и
функции
дифференцируемы в этой точке, то и
функции
![]() дифференцируемы в точке
дифференцируемы в точке
![]() .
Следовательно, выполняется условие 1)
теоремы 3. Покажем,
что выполнено и условие 2) теоремы 3. Для
этого надо показать, что из (6) следует
(1).
.
Следовательно, выполняется условие 1)
теоремы 3. Покажем,
что выполнено и условие 2) теоремы 3. Для
этого надо показать, что из (6) следует
(1).
Имеем,
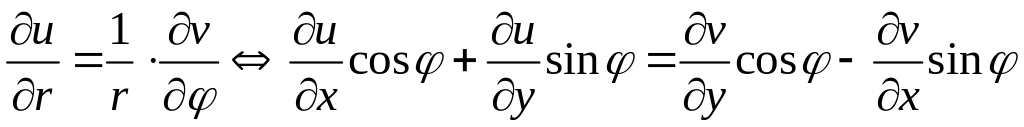 .
.
Значит,
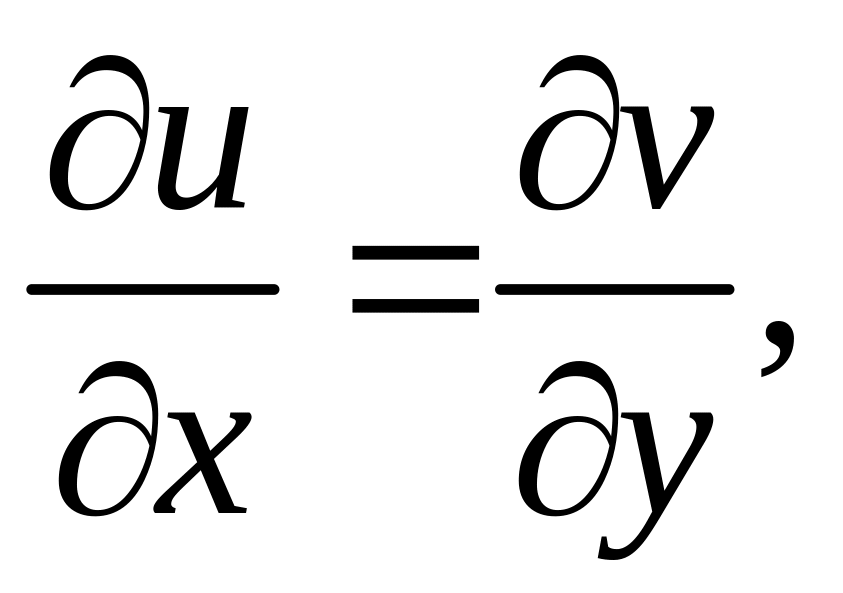 .
.
А
также из условия
имеем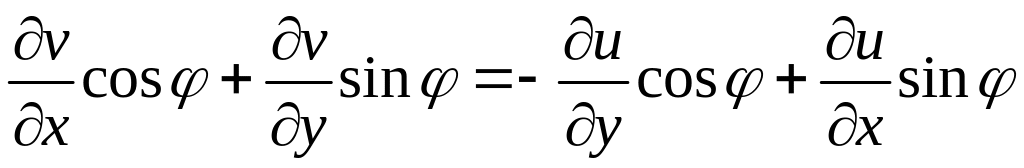 .
.
Отсюда
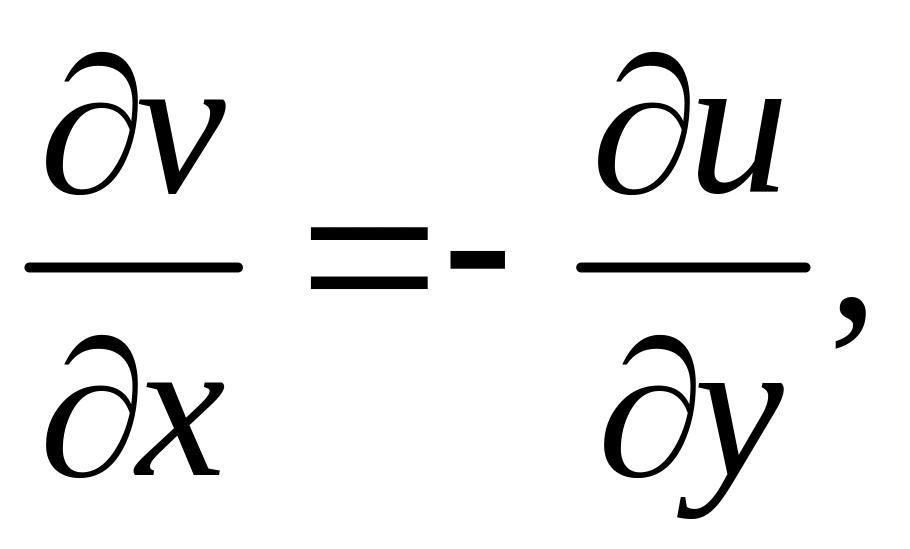
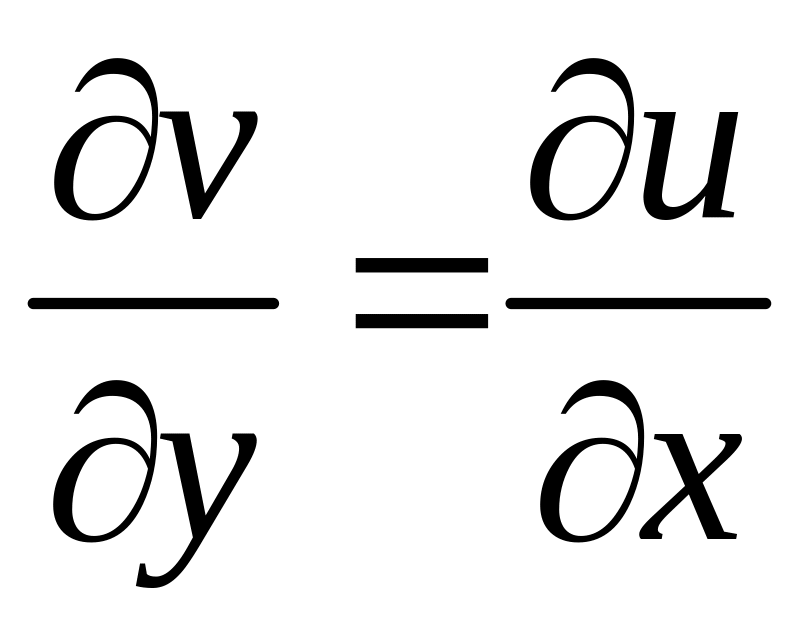 .
.
Итак,
выполнены условия 1) и 2) теоремы 3.
Следовательно,
функция
f(z)
дифференцируема в точке
![]() .
.
