§6. Геометрическая интерпретация функции комплексного переменного

Пусть w=f(z) задана на D. E - множество её значений. То есть каждой точке z=x+iy D ставится в соответствие точка w=f(z)=u+iv. Удобнее рассматривать две комплексные плоскости и , а функцию w=f(z) - как отображение из в . Часто считают, что плоскости и – одна и та же плоскость , тогда f задаёт отображение из в себя.

Пусть L D – некоторая кривая в плоскости . Eё образом при отображении f является некоторое множество точек К, которое может и не быть кривой. Пусть кривая в задана параметрически:

Т ак как отображение f задается равенствами: то образ кривой L имеет параметрические уравнения:

Образом области может и не быть область.

Пример1. Найти образ окружности х²+y²=4 при отображении .

∆ z=х+i∙y; х²+y²= ², следовательно, х²+y²=4 ²=4, =2.

Из уравнения следует . Значит, окружность =2 перейдет в - окружность. ∆

Пример2. Найти образ прямой х=а при отображении .

∆ Зададим прямую параметрически:

Так как z=х+i∙y, то z=а+i∙t – комплексное уравнение прямой.

При отображении получим:

- комплексное уравнение образа прямой.

Так как w=u+i∙v, то - параметрическое уравнение образа.

Выясним, что геометрически выражают эти уравнения. Исключим параметр t из уравнений: .

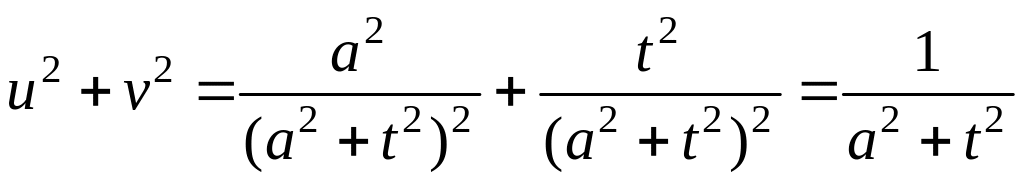Так как (из первого уравнения), то - преобразуем:

, ,

- уравнение окружности с центром .

Если t изменяется от - ∞ до 0, то u изменяется от 0 до , а v – от +0 до +0. Следовательно, описывается верхняя половина окружности от точки (0; 0) до точки . Если t изменяется от 0 до + ∞, то u изменяется от до +0, а v – от -0 до -0, т.е. описывается нижняя половина окружности от точки до (0; 0).

Итак, образом прямой х=а является окружность с выколотой точкой (0; 0), в которую переходит точка ∞.

§7.Дифференцирование функции одной комплексной переменной

1.Производная функции комплексной переменной

Пусть функция w=f(z) определена в окрестности точки z₀ U(z₀). Придадим точке z₀ произвольное приращение так, чтобы z₀+∆zU(z₀). Тогда функция получит приращение: .

Составим отношение (функция от ∆z).

Определение 1. Если существует конечный , то он называется производной функции f в точке z₀, и обозначается .

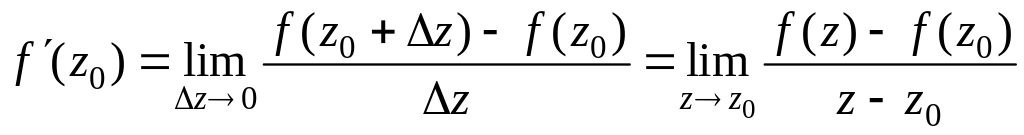
(при любом стремлении z к z₀ в комплексной плоскости).

Пример. f(z)=z² вычислить z₀ .

∆ Придадим точке z₀ произвольное приращение , получим точку z=z₀+∆z, , . ∆

Определение 2. Функция f(z) называется дифференцируемой в точке z₀, если ее приращение в этой точке можно представить в виде , где (не зависит от ∆z), .

Теорема 1. Функция f(z) дифференцируема в точке z₀ тогда и только тогда, когда существует конечная производная функции в точке z₀, причем =А.

Доказательство.

1) Необходимость.

Пусть f(z) дифференцируема в точке z₀. Тогда по определению ее приращение , где .

, т.е. =А, .

2) Достаточность.

Пусть существует = . Тогда = + , где . Тогда . Так как не зависит от ∆z, , то функция по определению непрерывна в точке z₀.

Определение 2 (эквивалентно определению 2). Функция f(z) называется дифференцируемой в точке z₀, если в этой точке она имеет конечную производную.

Определение. Функция f(z) называется дифференцируемой в области G, если она дифференцируема в каждой точке z этой области.

Пусть f(z) дифференцируема в области G. Тогда любой точке z G можно поставить в соответствие число . Такое соответствие является функцией, которую называют производной от f(z) на G. Обозначается .

Теорема 2 (необходимое условие дифференцируемости). Если функция f(z) дифференцируема в точке z₀, то она непрерывна в этой точке.

Доказательство.

Так как f(z) дифференцируема в точке z₀, то по определению

, .

Тогда . Значит, по определению, f(z) дифференцируема в точке z₀.

Замечание. Теорема, обратная теореме 2, неверна. Оказывается, среди непрерывных функций комплексного переменного легко найти функции, которые будут определены и непрерывны на , но не имеют производной ни в одной точке комплексной плоскости.

Пример.  , u(x;y)=x, v(x;y)=-y.

u и v – непрерывные функции на , следовательно, f(z) - непрерывна на .

Пусть z - произвольная точка. Придадим z приращение . Тогда

= .

. Покажем, что не существует. Обозначим .

1) Выберем последовательность точек : , т.е. по оси Ох.

Тогда .

2) Выберем последовательность точек : , т.е. по оси Оy.

Тогда .

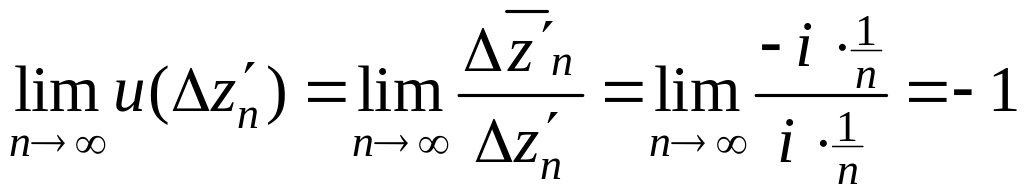Так как для двух разных последовательностей и , стремящихся к 0, соответствующие последовательности значений функции и имеют разные пределы, то в точке z не существует. Т.к. z – произвольная точка, то не существует в одной точке комплексной плоскости.

Следовательно, функция не имеет производной ни в одной точке, комплексной плоскости. 

Так как определение производной в по форме такие же, как и в , и основные свойства пределов переносятся из в , то в остаются в силе основные правила дифференцирования:

1. .

2. .

3. .

4. , g(z)0.

5. Производная сложной функции. Пусть w=f(t), где t=g(z). Тогда

.

6. Производная обратной функции.

w=f(z), D(f) – область определения, E(f) – множество значений. непрерывна на E. Пусть w₀=f(z₀). Если дифференцируема в точке z₀ и , то дифференцируема в точке w₀=f(z₀) и .

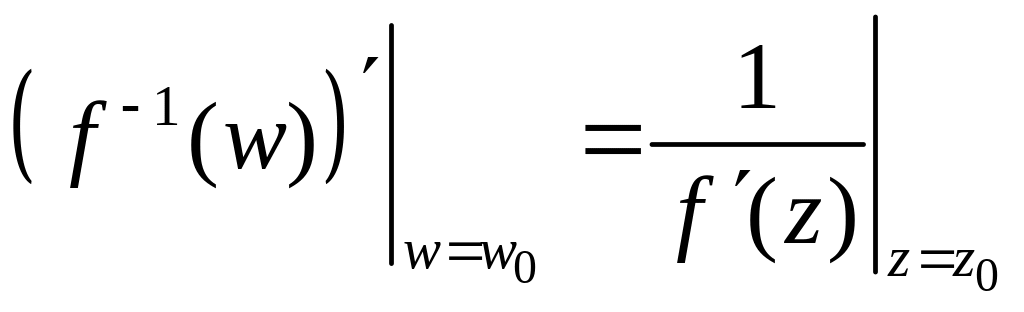7. =с, .

8. =z, .

9. , n .

Определение. Производной второго порядка от функции комплексного переменного называется производная от ее производной первого порядка:

, и т.д, .