
- •§1. Комплексные числа и действия над ними
- •1.Понятие комплексного числа. Действия над комплексными числами
- •2. Геометрическая интерпретация комплексного числа.
- •3. Комплексная плоскость как метрическое пространство
- •§2.Последовательности комплексных чисел. Предел последовательности
- •§3. Расширенная комплексная плоскость
- •§4. Функции комплексного переменного
- •1. Комплексно-значные функции действительной переменной
- •2. Кривые на комплексной плоскости
- •3.Функции комплексного переменного
- •§5. Предел и непрерывность функции комплексного переменного
- •1. Предел функции комплексного переменного
- •2.Непрерывность функции комплексного переменного
- •§6. Геометрическая интерпретация функции комплексного переменного
- •§7.Дифференцирование функции одной комплексной переменной
- •1.Производная функции комплексной переменной
- •2. Необходимые и достаточные условия
- •3. Понятие аналитической функции
- •4. Гармонические функции
- •5. Восстановление аналитической функции
- •6. Геометрический смысл аргумента и модуля производной
- •7. Понятие о конформном отображении
- •§8. Простейшие элементарные функции комплексной переменной
- •1. Линейная функция
- •2. Дробно-линейная функция
- •3.Многочлен
- •4. Показательная функция
- •5. Тригонометрические функции
- •6. Гиперболические функции
- •7. Области однолистности аналитических функций. Обратные функции
- •8. Степенная функция и радикал
- •9. Логарифмическая функция
- •10. Общие степенная и показательная функции
- •§9. Интегрирование функций комплексного переменного
- •1.Понятие интеграла
- •2.Вычисление интеграла от функции комплексного переменного
- •3.Основные свойства интеграла от функции комплексного переменного
- •§10. Интегральная теорема Коши
- •§11. Первообразная
- •§12. Интегральная формула Коши и ее следствия
- •1. Интегральная формула Коши
- •2. Бесконечная дифференцируемость аналитической функции
- •3. Теорема Морера
- •4. Теорема о среднем
- •5. Принцип максимума модуля аналитической функции
2. Кривые на комплексной плоскости
Пусть дана непрерывная комплексно-значная функция
z=λ(t), t[α,β]. (1)
В этом случае на комплексной плоскости задана непрерывная кривая z=λ(t), t[α,β] (это общее уравнение кривой).
Параметрическое уравнение кривой на комплексной плоскости:
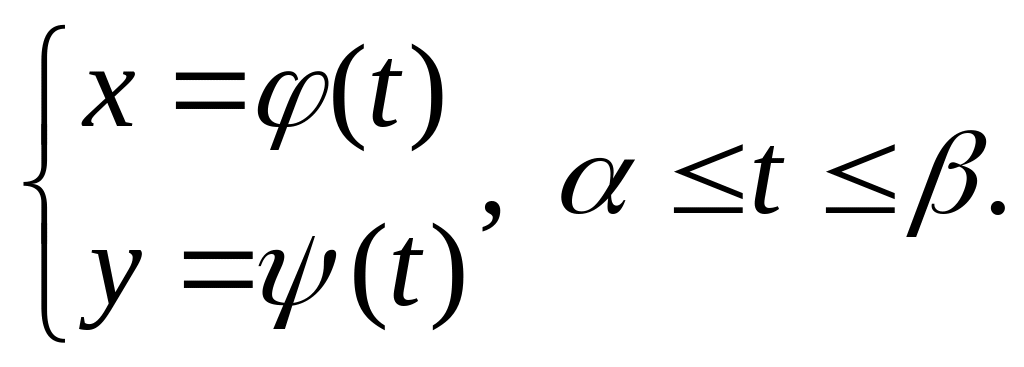
Кривая (1) является упорядоченным множеством точек комплексной плоскости, ориентированным в направлении возрастания параметра t. Направление движения точки z вдоль кривой в направлении возрастания параметра t называется положительным.
Точка а=λ(α) – начало, а b=λ(β) – конец кривой.
Кривая (1), у которой начальная и конечная точка совпадают, называется замкнутой.
Кривая
называется гладкой,
если λ(t)
непрерывно дифференцируема на [α,β]
и
![]() на [α,β].
При этом если кривая замкнутая, то
должно выполняться
на [α,β].
При этом если кривая замкнутая, то
должно выполняться
![]() .
.
Гладкая кривая во всех точках имеет касательную.
Кривая
называется кусочно-гладкой,
если λ(t)
непрерывна, и кривую можно разбить на
конечное число гладких кривых.
Кусочно-гладкая кривая спрямляема и
её длина равна
![]() .
.
Пример. Получим комплексное уравнение окружности с центром в точке (a,b) и радиуса R.
Δ
Параметрические уравнения:
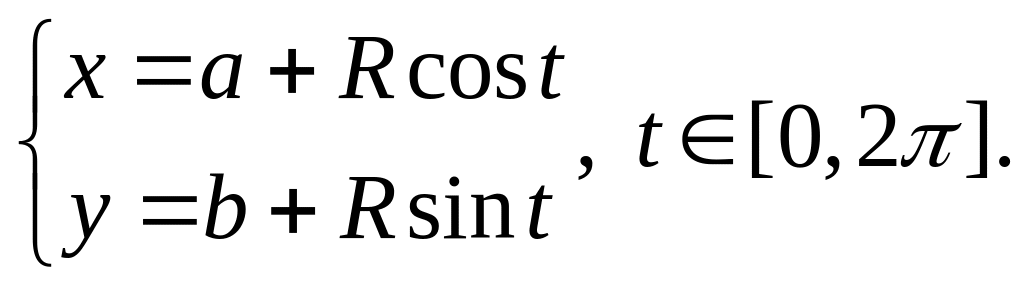
Тогда z=λ(t)=x+iy=a+Rcost+i(b+Rsint)=a+ib+R(cost+isint).
Обозначим z0=a+ib. По формуле Эйлера eit=cost+isint. Тогда
z=z0+Reit,
![]() -
уравнение окружности с центром в точке
z0=(a,b)
и радиусом R
на комплексной плоскости. Δ
-
уравнение окружности с центром в точке
z0=(a,b)
и радиусом R
на комплексной плоскости. Δ
3.Функции комплексного переменного
Определение.
Функцией
комплексной переменной
называется отображение f
некоторого подмножества D
комплексной плоскости во множество
![]() .
.
f:
D![]() →
.
→
.
При этом множество D называется областью определения функции f. Обозначается w=f(z).
w – образ точки z при отображении f, z – прообраз точки w при отображении f.
Пусть
![]() .
Образом множества E
при отображении f
является
.
Образом множества E
при отображении f
является
![]() .
.
Тогда f(D) называется множеством значений функции f. Для функции комплексной переменной вводят понятие инъективности, сюрьективности и биективности отображения, как и для функции действительной переменной.
Примеры.
Δ 1) w=|z|, w=z2+i, w=Rez, w=Imz. Областью определения всех этих функций является .
2)
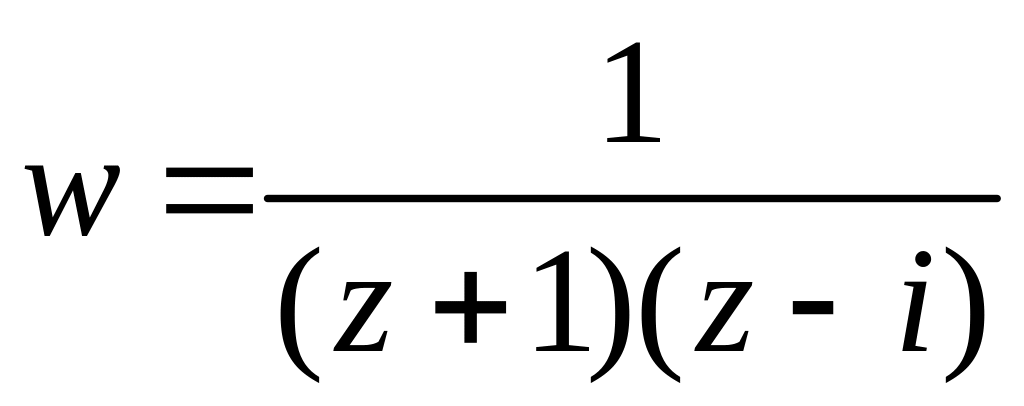 ,
D(w)=
\
,
D(w)=
\![]() .
Δ
.
Δ
Пусть
![]() .
Положим
z=x+iy,
w=u+iv,
x,
y,
u,
v
.
Положим
z=x+iy,
w=u+iv,
x,
y,
u,
v![]()
![]() .
.
Значение w зависит от x,y. Следовательно, функции u, v зависят от x и y, то есть u=u(x,y), v=v(x,y) – действительные функции двух действительных переменных. Таким образом, любой функции комплексной переменной соответствует пара действительных функций двух действительных переменных. Верно и обратное: любой паре действительных функций двух действительных переменных можно сопоставить функцию f(z)=f(x+iy)=u(x,y)+iv(x,y). Функция u(x,y) называется действительной частью, v(x,y) – мнимой частью функции w=f(z).
Примеры.
Δ 1) f(z)=|z|. Пусть z=x+iy. Тогда
f(z)=|x+iy|=![]() .
.
2)
w=f(z)=z2,
z=x+iy,
w=(x+iy)2=x2-y2+i2xy
![]() Ref(z)=x2-y2,
Imf(z)=2xy.
Ref(z)=x2-y2,
Imf(z)=2xy.
3) Найти функцию комплексной переменной (в виде w=f(z)), действительные и мнимые части которой соответственно равны:
 ,
,
w=f(z)=f(x+iy)=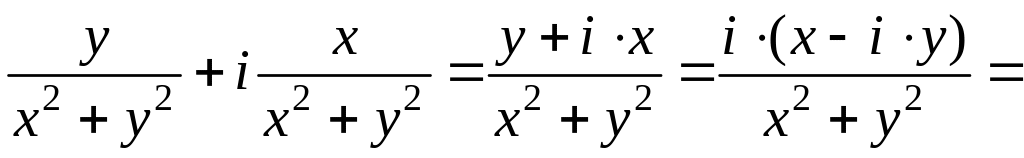
 .
.
Следовательно,
![]() .
.
Если
каждому z
соответствует лишь одно значение
w=f(z),
то функция называется однозначной
(w=|z|,
w=![]() ,
w=Rez
и т.д.) Если некоторым z
соответствует более чем одно значение
w,
функция называется многозначной
(
,
w=Rez
и т.д.) Если некоторым z
соответствует более чем одно значение
w,
функция называется многозначной
(![]() - n-значная
функция,
w=Argz
– бесконечно
- значная функция).
- n-значная
функция,
w=Argz
– бесконечно
- значная функция).
