
- •§1. Комплексные числа и действия над ними
- •1.Понятие комплексного числа. Действия над комплексными числами
- •2. Геометрическая интерпретация комплексного числа.
- •3. Комплексная плоскость как метрическое пространство
- •§2.Последовательности комплексных чисел. Предел последовательности
- •§3. Расширенная комплексная плоскость
- •§4. Функции комплексного переменного
- •1. Комплексно-значные функции действительной переменной
- •2. Кривые на комплексной плоскости
- •3.Функции комплексного переменного
- •§5. Предел и непрерывность функции комплексного переменного
- •1. Предел функции комплексного переменного
- •2.Непрерывность функции комплексного переменного
- •§6. Геометрическая интерпретация функции комплексного переменного
- •§7.Дифференцирование функции одной комплексной переменной
- •1.Производная функции комплексной переменной
- •2. Необходимые и достаточные условия
- •3. Понятие аналитической функции
- •4. Гармонические функции
- •5. Восстановление аналитической функции
- •6. Геометрический смысл аргумента и модуля производной
- •7. Понятие о конформном отображении
- •§8. Простейшие элементарные функции комплексной переменной
- •1. Линейная функция
- •2. Дробно-линейная функция
- •3.Многочлен
- •4. Показательная функция
- •5. Тригонометрические функции
- •6. Гиперболические функции
- •7. Области однолистности аналитических функций. Обратные функции
- •8. Степенная функция и радикал
- •9. Логарифмическая функция
- •10. Общие степенная и показательная функции
- •§9. Интегрирование функций комплексного переменного
- •1.Понятие интеграла
- •2.Вычисление интеграла от функции комплексного переменного
- •3.Основные свойства интеграла от функции комплексного переменного
- •§10. Интегральная теорема Коши
- •§11. Первообразная
- •§12. Интегральная формула Коши и ее следствия
- •1. Интегральная формула Коши
- •2. Бесконечная дифференцируемость аналитической функции
- •3. Теорема Морера
- •4. Теорема о среднем
- •5. Принцип максимума модуля аналитической функции
3. Комплексная плоскость как метрическое пространство
На множестве метрика задаётся следующим образом:
ρ(z1,z2)=|z1-z2|, z1,z2 .
Так как
|z1-z2|=![]() ,
то метрика в
совпадает с метрикой в
,
то метрика в
совпадает с метрикой в
![]() .
В метрическом пространстве
естественным
образом вводятся характерные для
метрического пространства понятия
окрестности, внутренней, внешней,
граничной, предельной точки, открытого,
замкнутого, ограниченного множества,
области и другие.
.
В метрическом пространстве
естественным
образом вводятся характерные для
метрического пространства понятия
окрестности, внутренней, внешней,
граничной, предельной точки, открытого,
замкнутого, ограниченного множества,
области и другие.
§2.Последовательности комплексных чисел. Предел последовательности
Пусть {zn}: z1, z2, …, zn, … - последовательность комплексных чисел.
Определение.
Комплексное число z0
называется пределом
числовой последовательности {zn},
если ρ(zn
,z0)=|zn-z0|![]() 0.
0.
Это можно записать следующим образом:
![]() ε>0
N
ε>0
N![]() :
n>N
|zn-z0|<ε.
:
n>N
|zn-z0|<ε.
Геометрический смысл. Точка z0 является предельной точкой последовательности {zn}, если какой бы малый круг радиуса ε с центром в точке z0 ни взять, всегда можно указать номер N, начиная с которого все члены последовательности лежат в этом круге.
Определение. Если последовательность {zn} имеет конечный предел, то она называется сходящейся.
Теорема
1.
![]() .
.
Доказательство.
![]() 1) Пусть
1) Пусть
![]() .
Тогда ε>0
N
:n>N
выполнено
|zn-z0|<ε.
.
Тогда ε>0
N
:n>N
выполнено
|zn-z0|<ε.
Так как
|Re(zn-z0)|≤|zn-z0|<ε,
то
![]() ,
отсюда
,
отсюда
![]() .
.
Так как
|Im(zn-z0)|≤|zn-z0|<ε,
то
![]() ,
отсюда
,
отсюда
![]() .
.
2) Пусть и .
По
определению ε>0
N1![]() :
n>N1
|Rezn–Rez0|=|Re(zn-z0)|<
:
n>N1
|Rezn–Rez0|=|Re(zn-z0)|<![]() ,
,
ε>0 N2 : n>N2 |Imzn–Imz0|=|Im(zn-z0)|< .
Пусть N=max{N1,N2}. Тогда n>N для выбранного ε>0
|zn-z0|<|Re(zn-z0)|+|Im(zn-z0)|<![]() ,
следовательно
.
,
следовательно
.
![]()
Пример
1. ∆
а)
 ;
;
![]() .
.
б)
![]() .
Т.к.
.
Т.к.
![]() не существует, то
не существует, то
![]() не существует. ∆
не существует. ∆
Для решения вопроса о сходимости { zn} можно рассмотреть вместо последовательностей {Rezn} и {Imzn} так же последовательности {|zn |} и {arg zn}. Рассмотрим в начале пример.
Пример
2.
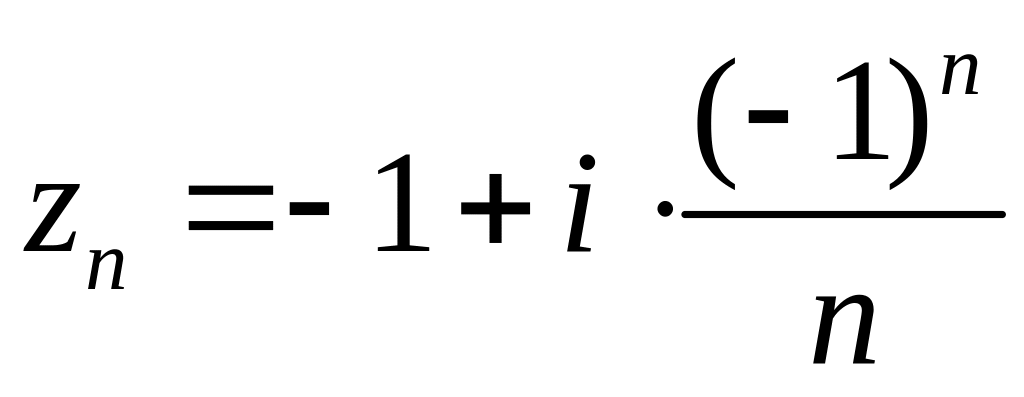 .
.
∆ По
теореме 1
![]() .
Покажем, что, однако, {arg
zn}
– расходится.
.
Покажем, что, однако, {arg
zn}
– расходится.
Если
n=2k,
то
![]() .
Следовательно,
.
Следовательно,
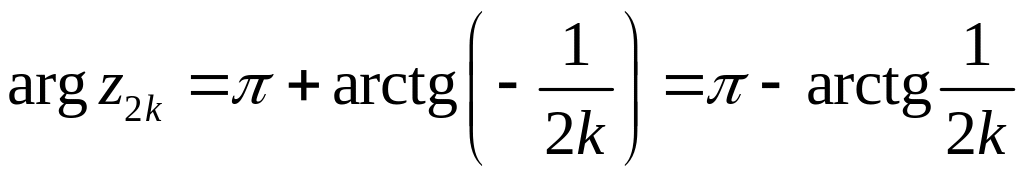 .
.
Если
n=2k+1,
то
![]() .
Следовательно,
.
Следовательно,
![]() .
.
![]() ,
,
![]() .
Следовательно,
.
Следовательно,
![]() не
существует.
не
существует.
Итак,
из того, что
![]() ,
в общем случае не
следует,
что
,
в общем случае не
следует,
что
![]() .
Но и здесь можно найти сходящуюся
последовательность {Arg
zn
},
сходящуюся к Arg
z
=π
. Обозначим через φn
значение Arg
zn
,
заключённое между 0 и 2π:
0<φn<2π.
Тогда, очевидно,
.
Но и здесь можно найти сходящуюся
последовательность {Arg
zn
},
сходящуюся к Arg
z
=π
. Обозначим через φn
значение Arg
zn
,
заключённое между 0 и 2π:
0<φn<2π.
Тогда, очевидно,
![]() ,
,![]() .
Следовательно,
.
Следовательно,
![]() .
.
Итак, для значения Arg z=π существует последовательность {Arg zn } сходящаяся к π. ∆
Теорема 2. Пусть {zn} - последовательность комплексных чисел.
1) Если
![]() и
и
![]() ,
то
,
то ![]() .
.
2) Если , то
а)
![]() ,
,
б) если
z0,
то φ
=Arg
z
φn={Arg
zn
}:
![]() .
В частности, если
.
В частности, если
![]() ,
то
.
,
то
.
Доказательство.
![]() 1)
Так как
1)
Так как
![]() ,
,
![]() то
то
![]() ,
, ![]() .
.
Тогда
по теореме 1
![]() .
.
2) а) Так
как
,
то
по теореме 1
![]() .
.
Тогда
![]() .
.
б) Пусть
![]() и φ
– какое-либо значение Arg
z.
Тогда, начиная с некоторого N,
все члены последовательности {zn}
будут лежать внутри угла, образованного
лучами, наклоненными под углами φ-
и φ
– какое-либо значение Arg
z.
Тогда, начиная с некоторого N,
все члены последовательности {zn}
будут лежать внутри угла, образованного
лучами, наклоненными под углами φ-![]() и
φ+
к оси ОХ и содержащего точку z.
Поэтому для аргументов ArgzN+1,
Arg
zN+2
,…
можно выбрать значения φN+1,
φN+2,…
так, чтобы выполнялось условие |φN+n–φ|
.
и
φ+
к оси ОХ и содержащего точку z.
Поэтому для аргументов ArgzN+1,
Arg
zN+2
,…
можно выбрать значения φN+1,
φN+2,…
так, чтобы выполнялось условие |φN+n–φ|
.
В озьмем
также
φ1=Arg
z1,
φ2=Arg
z2,...,φN=ArgzN.
Тогда
получим последовательность φn.
Покажем, что
озьмем
также
φ1=Arg
z1,
φ2=Arg
z2,...,φN=ArgzN.
Тогда
получим последовательность φn.
Покажем, что
![]() .
.
ε: 0ε N1(ε)≥N такой, что точки последовательности {zn }, для которых nN1(ε), будут лежать внутри угла, образованного лучами, наклоненными к оси ОХ под углами φ-ε и φ+ε и содержащего точку z. Для них значения φn удовлетворяет условию: φ–εφnφ+ε |φn-φ|ε .
Отметим,
что если
![]() ,
то в качестве φ
и φn
можно
выбрать главные значения аргументов,
тогда получим
.
,
то в качестве φ
и φn
можно
выбрать главные значения аргументов,
тогда получим
.
![]()
Следствие.
![]()
![]() .
.
Теорема 3 (критерий Коши сходимости последовательности комплексных чисел).
Для
того, чтобы последовательность
комплексных чисел {zn}
сходилась, необходимо и достаточно,
чтобы ε>0
N![]() :
n>N,
m
выполнялось |zn+m–zn|<ε.
:
n>N,
m
выполнялось |zn+m–zn|<ε.
Доказательство.
1) Пусть
.
Тогда ε>0
N
:
n>N
выполняется |zn–z|<![]() .
.
Тогда |zn+m–zn|=|zn+m–z+z-zn|≤|zn+m–z|+|zn–z|< + =ε m .
2) Пусть
ε>0
N
:
n>N,
m
выполняется |zn+m–zn|<ε.
Тогда |Re(zn+m–zn)|=|Rezn+m
–Rezn|<ε
и |Im(zn+m–zn)|=|Imzn+m–Imzn|<ε.
Следовательно, последовательности
действительных чисел {Rezn
и {Imzn
фундаментальные. Согласно критерию
Коши сходимости последовательности
действительных чисел они сходятся
(последовательность фундаментальна
тогда и только тогда, когда она сходится).
То есть
![]() и
и
![]() Тогда по теореме 1
Тогда по теореме 1
![]() .
Следовательно, {zn
}
сходится.
.
Следовательно, {zn
}
сходится.
