
- •§1. Комплексные числа и действия над ними
- •1.Понятие комплексного числа. Действия над комплексными числами
- •2. Геометрическая интерпретация комплексного числа.
- •3. Комплексная плоскость как метрическое пространство
- •§2.Последовательности комплексных чисел. Предел последовательности
- •§3. Расширенная комплексная плоскость
- •§4. Функции комплексного переменного
- •1. Комплексно-значные функции действительной переменной
- •2. Кривые на комплексной плоскости
- •3.Функции комплексного переменного
- •§5. Предел и непрерывность функции комплексного переменного
- •1. Предел функции комплексного переменного
- •2.Непрерывность функции комплексного переменного
- •§6. Геометрическая интерпретация функции комплексного переменного
- •§7.Дифференцирование функции одной комплексной переменной
- •1.Производная функции комплексной переменной
- •2. Необходимые и достаточные условия
- •3. Понятие аналитической функции
- •4. Гармонические функции
- •5. Восстановление аналитической функции
- •6. Геометрический смысл аргумента и модуля производной
- •7. Понятие о конформном отображении
- •§8. Простейшие элементарные функции комплексной переменной
- •1. Линейная функция
- •2. Дробно-линейная функция
- •3.Многочлен
- •4. Показательная функция
- •5. Тригонометрические функции
- •6. Гиперболические функции
- •7. Области однолистности аналитических функций. Обратные функции
- •8. Степенная функция и радикал
- •9. Логарифмическая функция
- •10. Общие степенная и показательная функции
- •§9. Интегрирование функций комплексного переменного
- •1.Понятие интеграла
- •2.Вычисление интеграла от функции комплексного переменного
- •3.Основные свойства интеграла от функции комплексного переменного
- •§10. Интегральная теорема Коши
- •§11. Первообразная
- •§12. Интегральная формула Коши и ее следствия
- •1. Интегральная формула Коши
- •2. Бесконечная дифференцируемость аналитической функции
- •3. Теорема Морера
- •4. Теорема о среднем
- •5. Принцип максимума модуля аналитической функции
3. Теорема Морера
Согласно
теореме Коши если f(z)-аналитическая
на односвязной области D,
то она непрерывна на D
и для любого кусочно–гладкого замкнутого
контура LD
![]() .
Справедливо и обратное утверждение.
.
Справедливо и обратное утверждение.
Теорема (Морера). Если f(z) непрерывна в односвязной области D, и вдоль любого кусочно–гладкого замкнутого контура LD , то f(z) – аналитическая в D.
Доказательство.
Равенство
нулю интеграла
по любому кусочно–гладкому замкнутому
контуру LD
означает, что
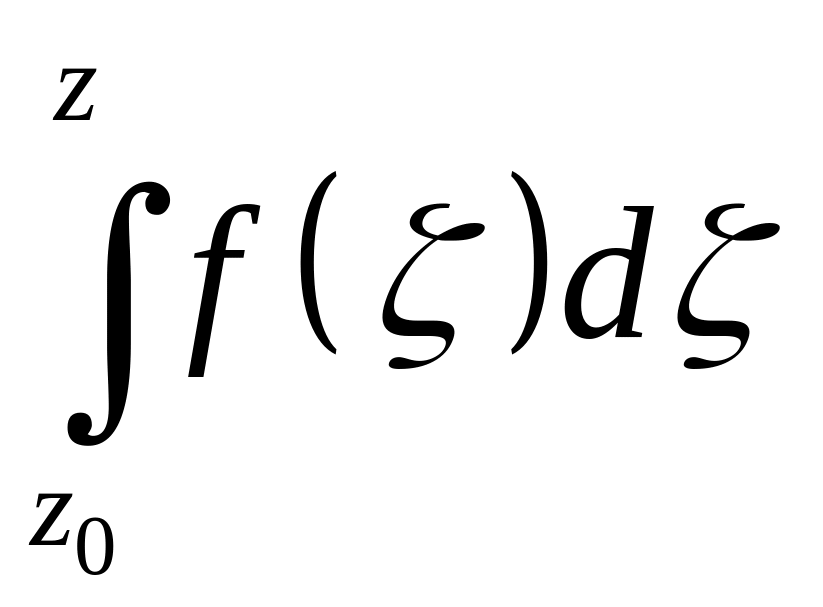 вдоль любой кривой, соединяющей точки
z0
и z
не зависит от вида кривой. Как было
доказано, функция
вдоль любой кривой, соединяющей точки
z0
и z
не зависит от вида кривой. Как было
доказано, функция
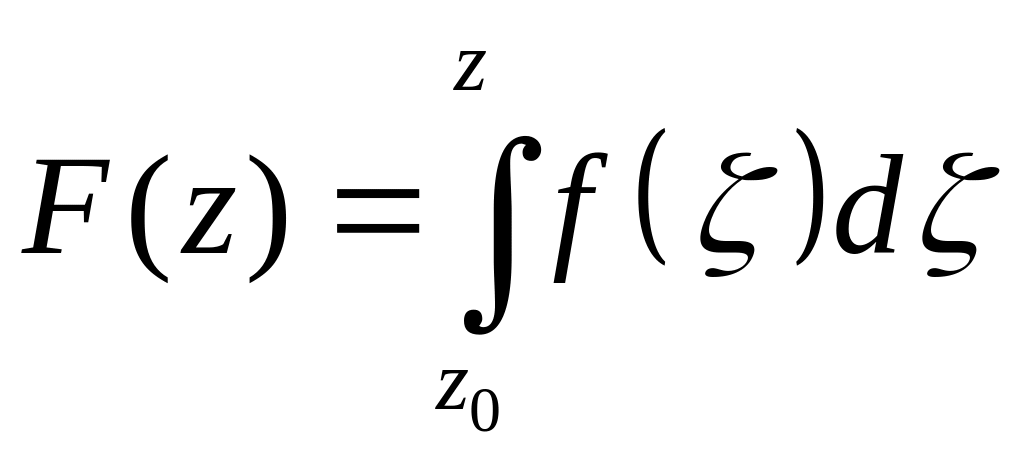 является аналитической в D,
причём F(z)=f(z).
Но по предыдущей теореме f(z)-аналитическая
функция, так как является производной
аналитической функции.
является аналитической в D,
причём F(z)=f(z).
Но по предыдущей теореме f(z)-аналитическая
функция, так как является производной
аналитической функции.
Определение. Функция f(z) непрерывная на односвязной области D, называется аналитической на D, если по любому кусочно–гладкому замкнутому контуру LD.
4. Теорема о среднем
Теорема. Значение аналитической функции f(z) в центре круга равно среднему арифметическому её значений на окружности этого круга, то есть, если z-z0r круг, лежащий в области G, f(z)-аналитическая в G, то
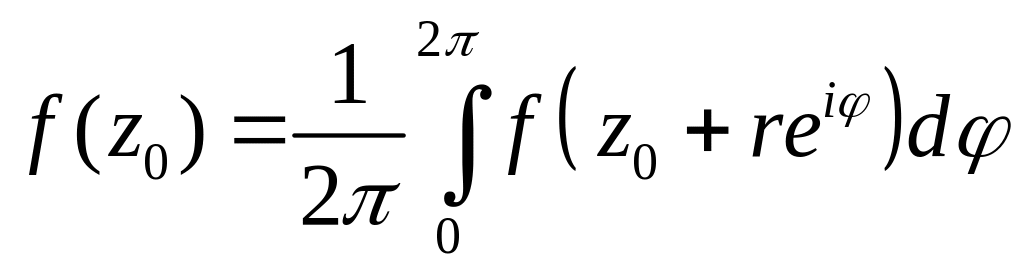 . (10)
. (10)
z=z0+rei, ([0,2])-уравнение окружности С с центром в точке z0, радиуса r.
По интегральной формуле Коши
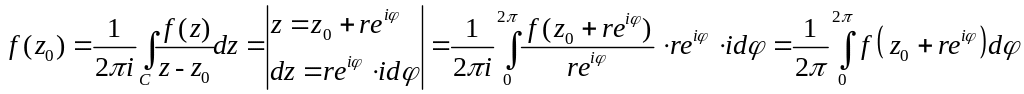 .
.
5. Принцип максимума модуля аналитической функции
Теорема. Модуль функции f(z),аналитической в некоторой области G и не равной тождественно константе, не может иметь максимума ни в одной точке этой области.
Доказательство.
Обозначим
![]() и предположим противное:
точка z0G:
f(z0)=M.
Из формулы (10) следует
и предположим противное:
точка z0G:
f(z0)=M.
Из формулы (10) следует
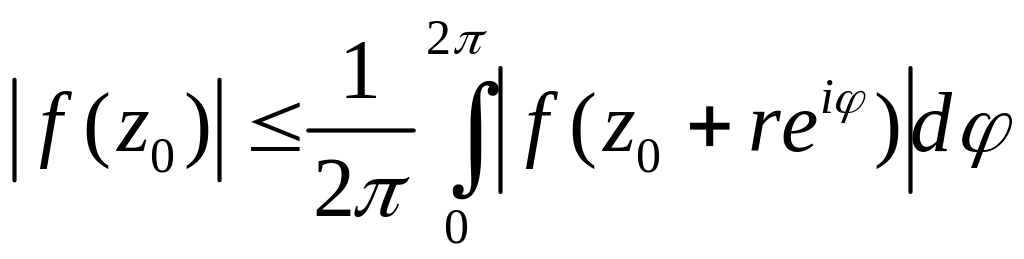 . (11)
. (11)
Так как
![]() ,
а f(z0)=M,
то из (11) следует, что
,
а f(z0)=M,
то из (11) следует, что
![]() .
.
Д ействительно,
если допустить, что при некотором
значении =0
ействительно,
если допустить, что при некотором
значении =0
![]() ,
то в силу непрерывности функции f(z)
неравенство
будет выполняться для любого
из
достаточно малого промежутка 0-0+,
а вне этого промежутка
.
Значит,
в этом случае правая часть неравенства
(11) должна быть меньше
M
,
то в силу непрерывности функции f(z)
неравенство
будет выполняться для любого
из
достаточно малого промежутка 0-0+,
а вне этого промежутка
.
Значит,
в этом случае правая часть неравенства
(11) должна быть меньше
M
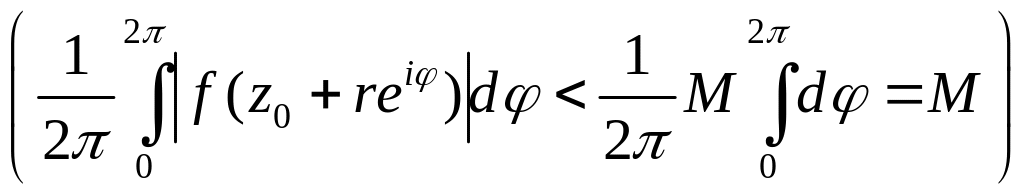 ,
а левая часть равна M
(f(z0)=M).
Этого быть не может. Следовательно,
если в некоторой точке z0
f(z0)=M,
то и в достаточно малой её окрестности
|z-z0|<r
.
,
а левая часть равна M
(f(z0)=M).
Этого быть не может. Следовательно,
если в некоторой точке z0
f(z0)=M,
то и в достаточно малой её окрестности
|z-z0|<r
.
П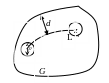 окажем
теперь, что f(z)=M
всюду в области G.
Пусть z1-
произвольная
точка области G.
Соединим точку z0
с точкой
z1
непрерывной линией L,
целиком лежащей в G.
Обозначим через d
расстояние от L
до границы области G.
Круг
с центром в произвольной точке кривой
L
радиусом
окажем
теперь, что f(z)=M
всюду в области G.
Пусть z1-
произвольная
точка области G.
Соединим точку z0
с точкой
z1
непрерывной линией L,
целиком лежащей в G.
Обозначим через d
расстояние от L
до границы области G.
Круг
с центром в произвольной точке кривой
L
радиусом
![]() принадлежит области G.
Следовательно, по доказанному f(z)=M
всюду внутри круга с центром в точке
z0
радиуса
принадлежит области G.
Следовательно, по доказанному f(z)=M
всюду внутри круга с центром в точке
z0
радиуса
![]() :
: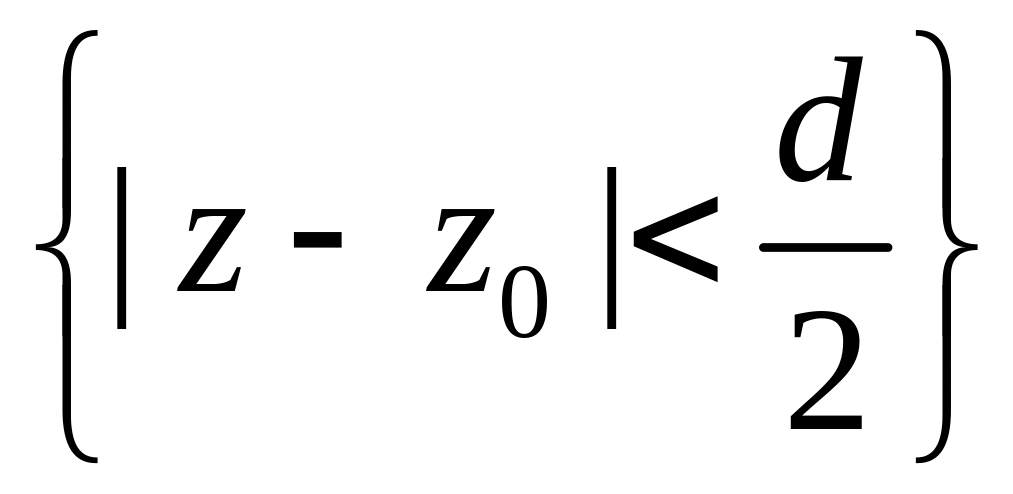 .
Пусть центр этого круга непрерывно
перемещается по L
от точки z0
к точке
z1.
Равенство
f(z)=M
должно выполняться всё время внутри
круга, каково бы ни
было положение центра круга. Следовательно,
в частности f(z1)=M.
Так как z1
-
произвольная точка области G,
то это означает, что f(z)=M
всюду в области G.
.
Пусть центр этого круга непрерывно
перемещается по L
от точки z0
к точке
z1.
Равенство
f(z)=M
должно выполняться всё время внутри
круга, каково бы ни
было положение центра круга. Следовательно,
в частности f(z1)=M.
Так как z1
-
произвольная точка области G,
то это означает, что f(z)=M
всюду в области G.
Покажем теперь, что в этом случае f(z)const.
![]() -
аналитическая функция.
-
аналитическая функция.
![]() ,
следовательно, по условиям Коши-Римана
получим, что
,
следовательно, по условиям Коши-Римана
получим, что
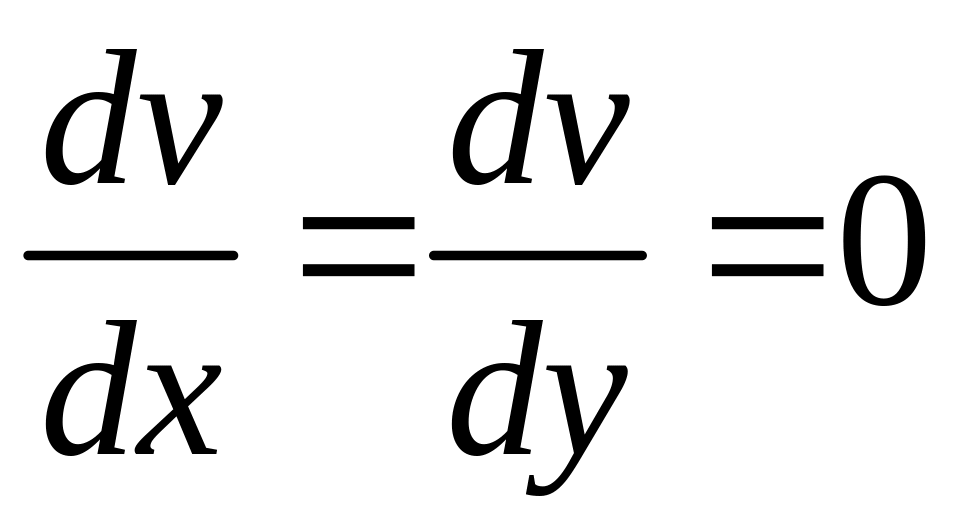 .
Следовательно, vconst.
Значит, и ln(f(z))const.
Поэтому f(z)const
в G.
.
Следовательно, vconst.
Значит, и ln(f(z))const.
Поэтому f(z)const
в G.
Получили противоречие с условием. Следовательно, предположение неверно, и аналитическая функция, не может иметь максимума модуля ни в одной точке области G.
Замечание.
Из
доказанного принципа следует, что если
f(z)-
аналитическая в области G
и
непрерывная в замкнутой области![]() ,
то максимум модуля достигается на
границе области G
при
условии, что f(z)
,
то максимум модуля достигается на
границе области G
при
условии, что f(z)![]() const.
В самом деле, так как f(z)-
непрерывная функция, то в замкнутой
области
она
принимает наибольшее значение в
некоторой точке z0
.Так
как точка z0
не может лежать в области
G
(по доказанной теореме), то она расположена
на границе области
G.
const.
В самом деле, так как f(z)-
непрерывная функция, то в замкнутой
области
она
принимает наибольшее значение в
некоторой точке z0
.Так
как точка z0
не может лежать в области
G
(по доказанной теореме), то она расположена
на границе области
G.
