
- •§1. Комплексные числа и действия над ними
- •1.Понятие комплексного числа. Действия над комплексными числами
- •2. Геометрическая интерпретация комплексного числа.
- •3. Комплексная плоскость как метрическое пространство
- •§2.Последовательности комплексных чисел. Предел последовательности
- •§3. Расширенная комплексная плоскость
- •§4. Функции комплексного переменного
- •1. Комплексно-значные функции действительной переменной
- •2. Кривые на комплексной плоскости
- •3.Функции комплексного переменного
- •§5. Предел и непрерывность функции комплексного переменного
- •1. Предел функции комплексного переменного
- •2.Непрерывность функции комплексного переменного
- •§6. Геометрическая интерпретация функции комплексного переменного
- •§7.Дифференцирование функции одной комплексной переменной
- •1.Производная функции комплексной переменной
- •2. Необходимые и достаточные условия
- •3. Понятие аналитической функции
- •4. Гармонические функции
- •5. Восстановление аналитической функции
- •6. Геометрический смысл аргумента и модуля производной
- •7. Понятие о конформном отображении
- •§8. Простейшие элементарные функции комплексной переменной
- •1. Линейная функция
- •2. Дробно-линейная функция
- •3.Многочлен
- •4. Показательная функция
- •5. Тригонометрические функции
- •6. Гиперболические функции
- •7. Области однолистности аналитических функций. Обратные функции
- •8. Степенная функция и радикал
- •9. Логарифмическая функция
- •10. Общие степенная и показательная функции
- •§9. Интегрирование функций комплексного переменного
- •1.Понятие интеграла
- •2.Вычисление интеграла от функции комплексного переменного
- •3.Основные свойства интеграла от функции комплексного переменного
- •§10. Интегральная теорема Коши
- •§11. Первообразная
- •§12. Интегральная формула Коши и ее следствия
- •1. Интегральная формула Коши
- •2. Бесконечная дифференцируемость аналитической функции
- •3. Теорема Морера
- •4. Теорема о среднем
- •5. Принцип максимума модуля аналитической функции
§12. Интегральная формула Коши и ее следствия
1. Интегральная формула Коши
Теорема. Пусть функция f(z) аналитическая в односвязной области D, L-произвольный замкнутый кусочно-гладкий контур, лежащий в D. Тогда для любой точки z0, лежащей внутри контура L, справедлива формула:
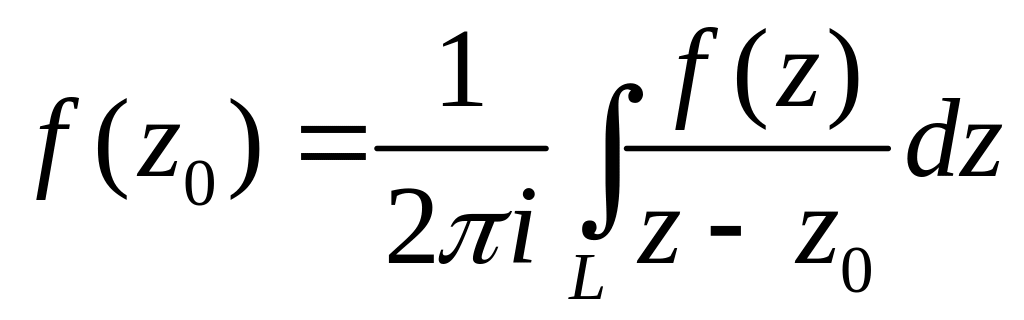 , (1)
, (1)
где L обходится в положительном направлении.
(1) - интегральная формула Коши. Она выражает значения аналитической функции внутри контура через её значения на контуре.
Доказательство.
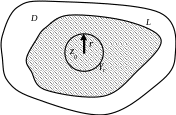 Пусть
z0-
произвольная точка, лежащая внутри
контура L.
Рассмотрим окружность γr:
|z-z0|=r
, где r
выберем так, чтобы γr
лежала внутри L.
В двусвязной области, ограниченной
контурами L
и
γr,
функция
Пусть
z0-
произвольная точка, лежащая внутри
контура L.
Рассмотрим окружность γr:
|z-z0|=r
, где r
выберем так, чтобы γr
лежала внутри L.
В двусвязной области, ограниченной
контурами L
и
γr,
функция
![]() является
аналитической, следовательно, она
аналитическая и на области
является
аналитической, следовательно, она
аналитическая и на области
![]() .
Тогда по следствию из теоремы Коши:
.
Тогда по следствию из теоремы Коши:
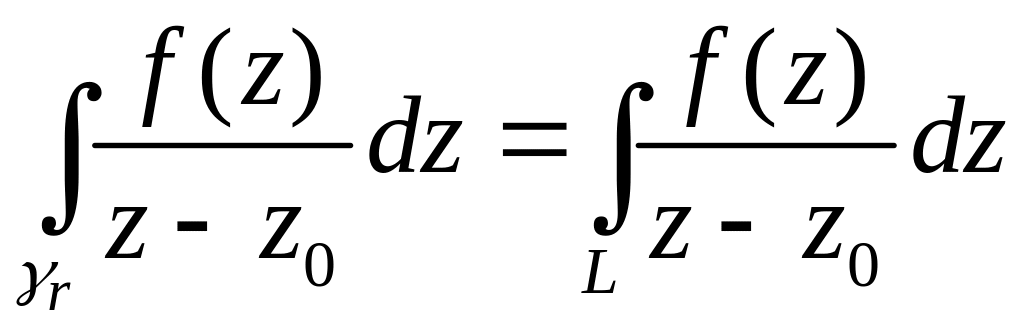 . (2)
. (2)
Из (2)
следует, что значение
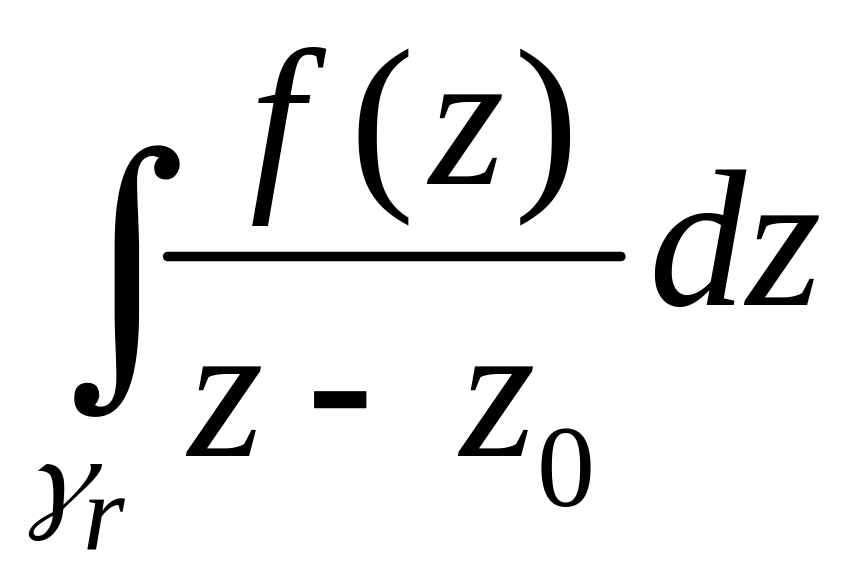 не
зависит от радиуса окружности γr.
не
зависит от радиуса окружности γr.
Из (2) следует, что для доказательства (1) достаточно показать, что
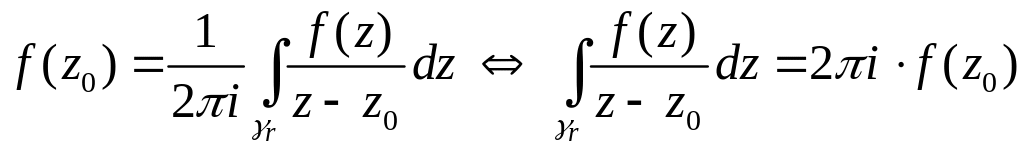 . (3)
. (3)
Так
как
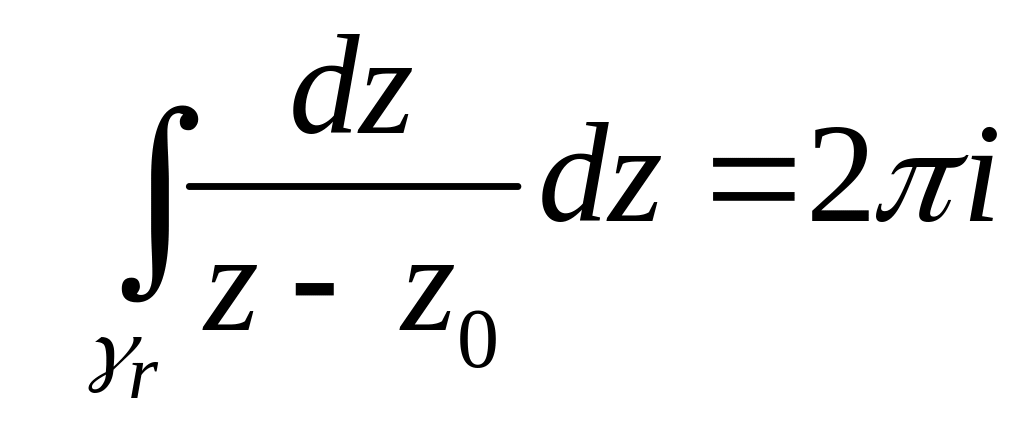 ,
то
,
то
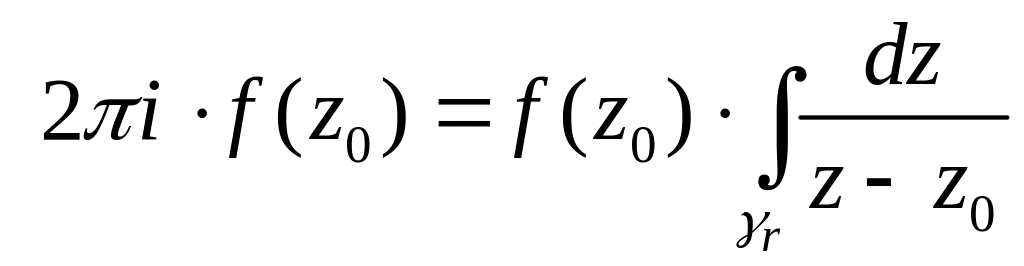 или
или
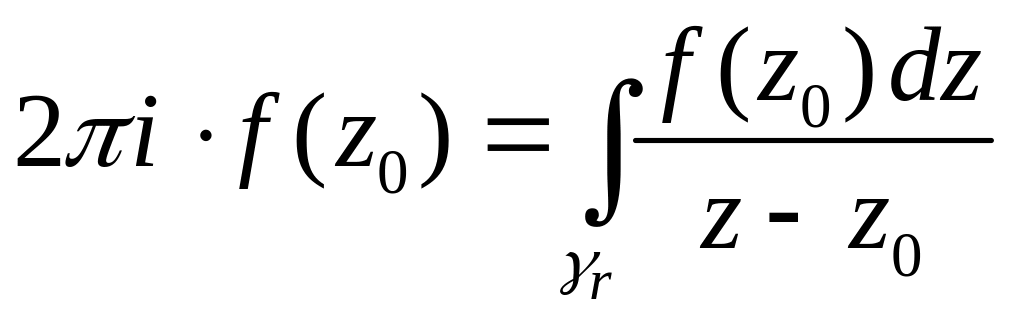 . (4)
. (4)
Из (3) и (4) следует, что для доказательства (1) надо доказать, что
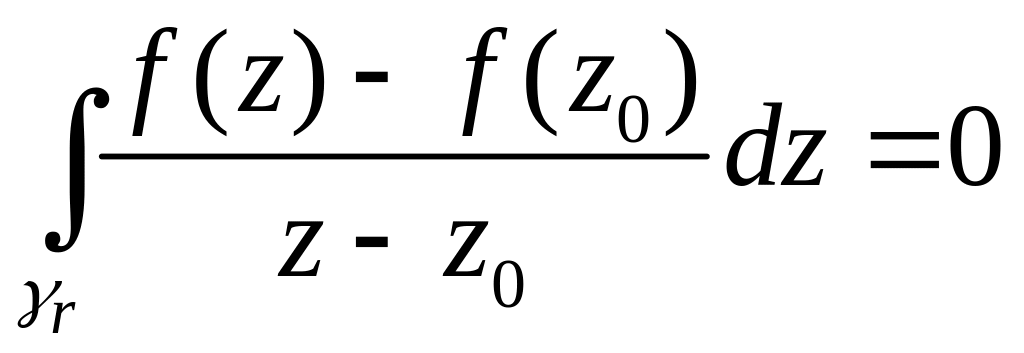 . (5)
. (5)
Заметим, что интеграл в (5) не зависит от r .
Возьмем
![]() .
Так как f(z)
аналитическая на D,
то f(z)
непрерывна в точке z0D.
Тогда
.
Так как f(z)
аналитическая на D,
то f(z)
непрерывна в точке z0D.
Тогда
![]() выполнено
выполнено
![]() .
.
Если
γr
такая, что r<δ,
то
![]() выполнено
|z-z0|=r<δ
|f(z)-f(z0)|<ε.
выполнено
|z-z0|=r<δ
|f(z)-f(z0)|<ε.
 . (6)
. (6)
Так как ε>0 – произвольное сколь угодно малое число, а значение интеграла не зависит от r, то (6) может быть выполнено только если , то есть выполнено (5), а значит, выполнено (1).
Следствие . Если две аналитические в односвязной области D функции f(z) и g(z) совпадают на замкнутом контуре LD, то они совпадают и внутри контура L.
Замечание.
Если
точка z0
лежит вне контура L,
то
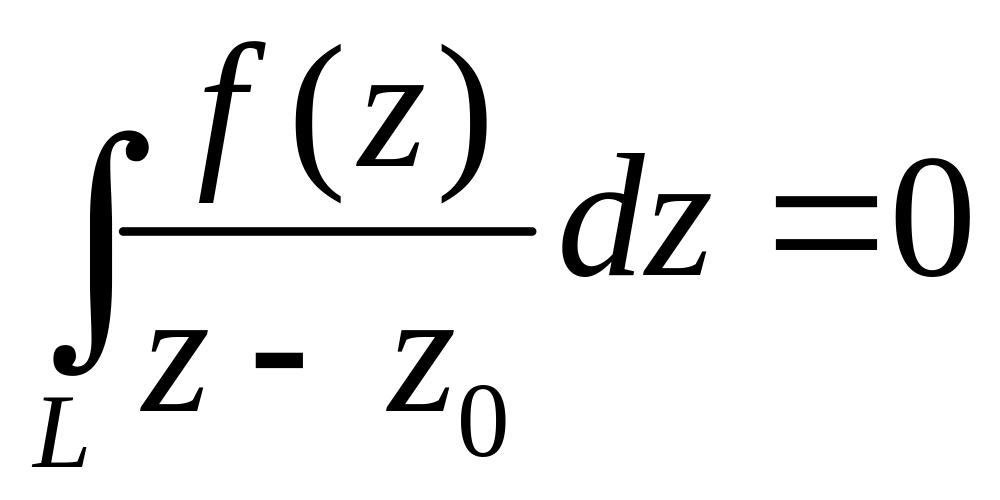 .
.
Действительно, в этом случае является аналитической не только на L, но и внутри L, следовательно, применима интегральная формула Коши, согласно которой этот интеграл равен 0.
Итак,

П ример.
а)
ример.
а)
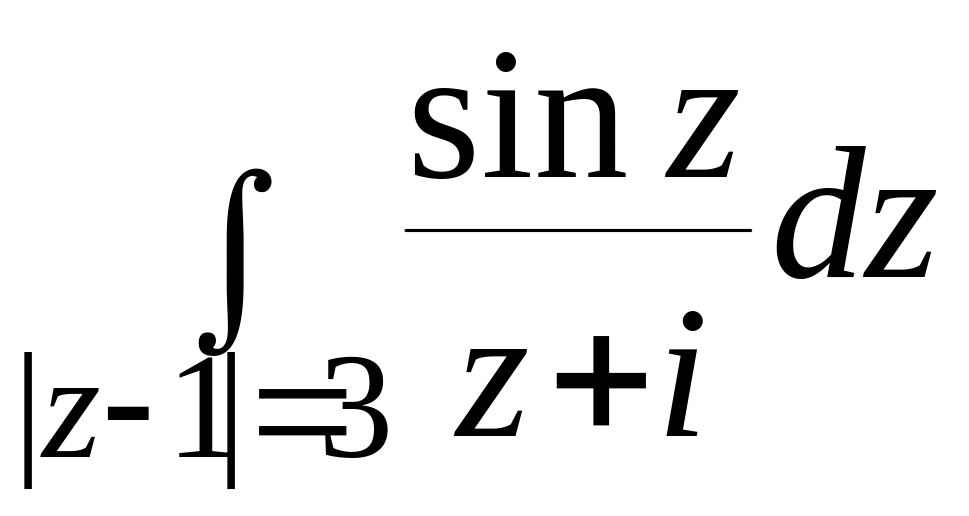 .
.
z0=-i лежит внутри окружности |z-1|=3, f(z)=sinz– аналитическая на , следовательно, по интегральной формуле Коши:
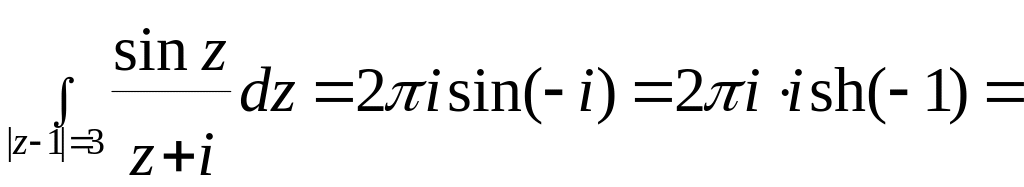
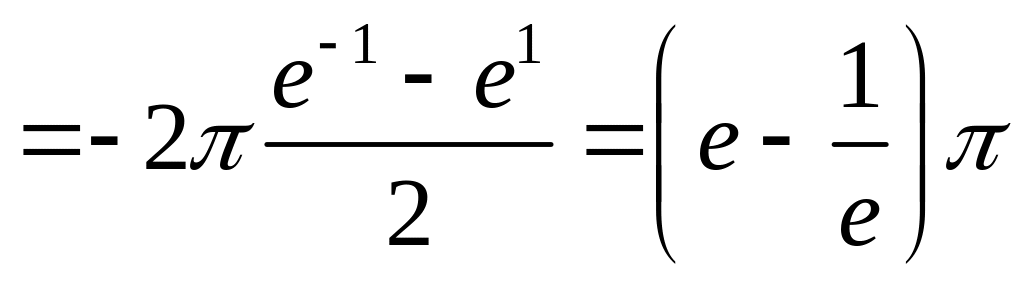 .
.
б)
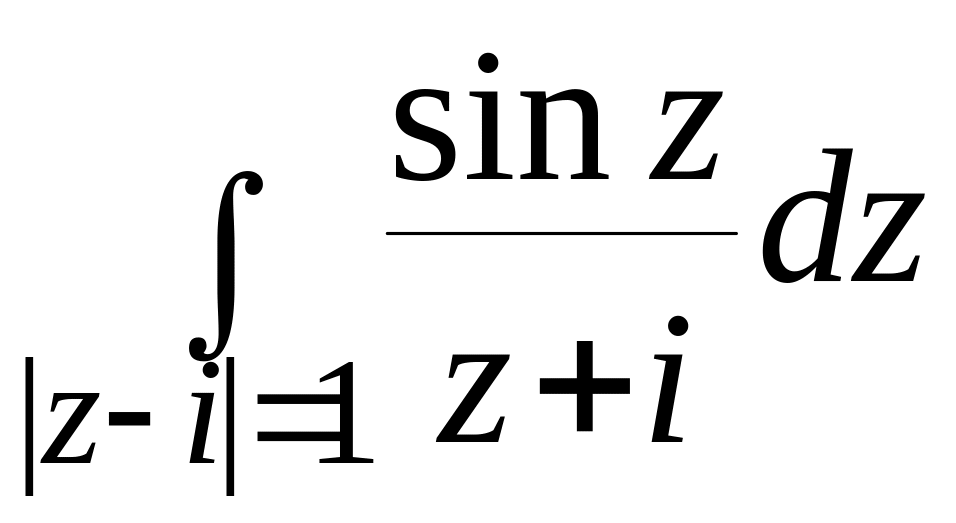 .
Функция
.
Функция
![]() аналитическая
в области
аналитическая
в области
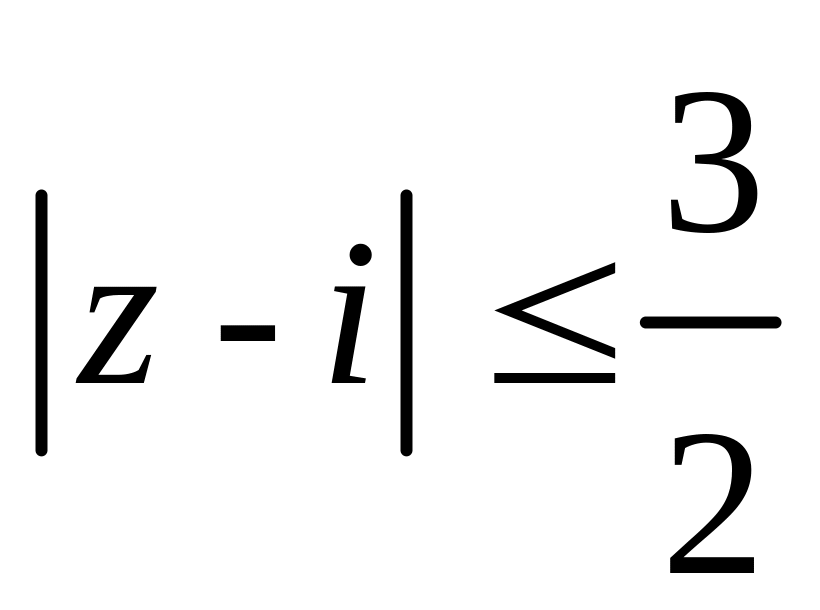 ,
содержащей окружность |z-i|=1,
следовательно, по интегральной формуле
Коши
=0.
,
содержащей окружность |z-i|=1,
следовательно, по интегральной формуле
Коши
=0.
2. Бесконечная дифференцируемость аналитической функции
Теорема. Всякая функция f(z), аналитическая в области D, имеет производные всех порядков на этой области, и для z0D справедлива формула:
 , (7)
, (7)
где L – произвольный кусочно-гладкий замкнутый контур, целиком лежащий в D и содержащий внутри себя точку z0.
Доказательство.
Проведем для n=1. Возьмем z0D и окружность γr: |z-z0|=r такую, чтобы γr находилась внутри L. Тогда и круг |z-z0|≤r будет целиком лежать в D. Применим интегральную формулу Коши:
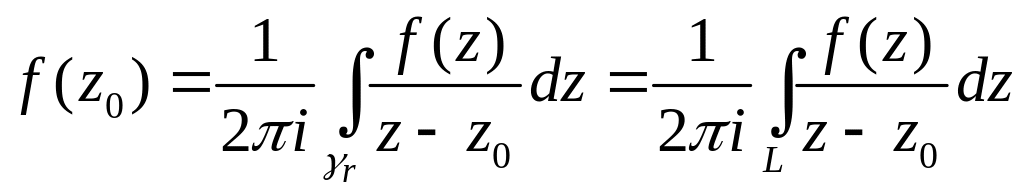 .
.
Возьмем
∆z:
z0+∆z![]() {z:|z-z0|≤r}.
Тогда
{z:|z-z0|≤r}.
Тогда
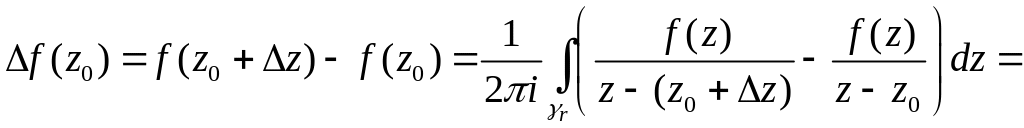
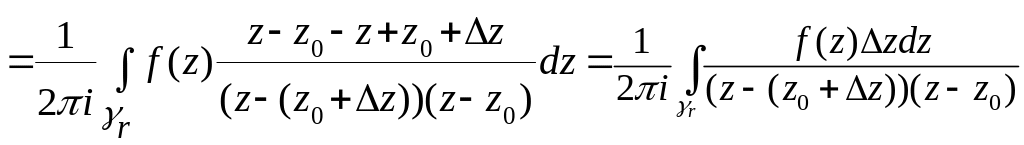 .
.
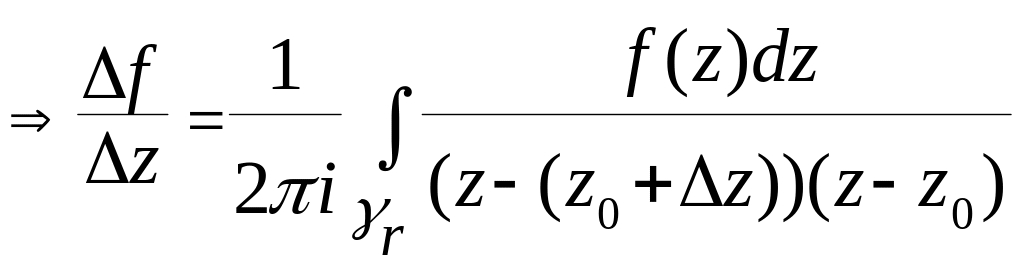 .
.
Покажем,
что
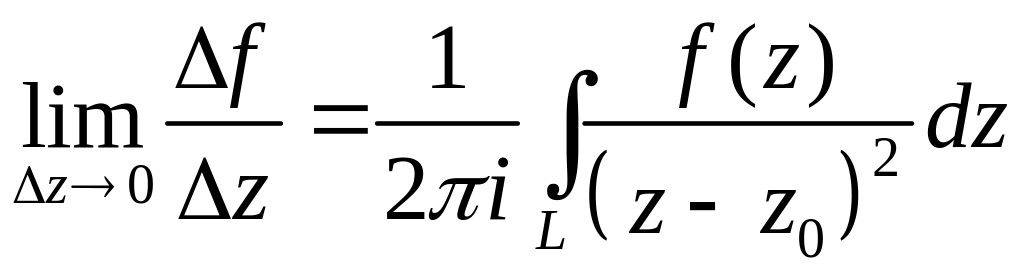 .
.
Рассмотрим
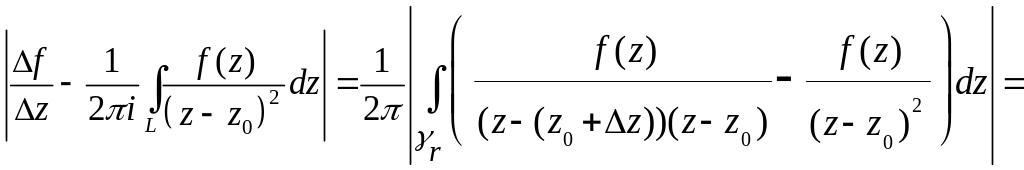
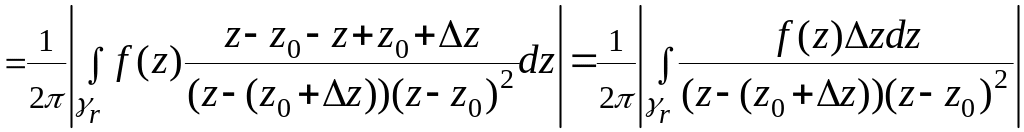 .
(8)
.
(8)
Так как
f(z)
аналитическая на D,
то она непрерывна на D.
Так как L-ограниченное
замкнутое множество, то f(z)
ограничена на L,
то есть
![]() .
.
![]() .
.
Тогда из (8) по свойству 5 получим:
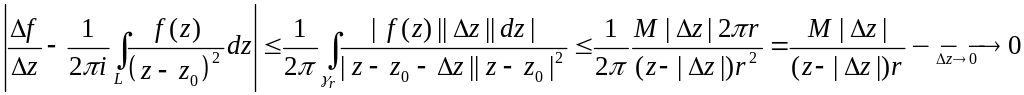 Следовательно,
.
Следовательно,
.
То
есть,
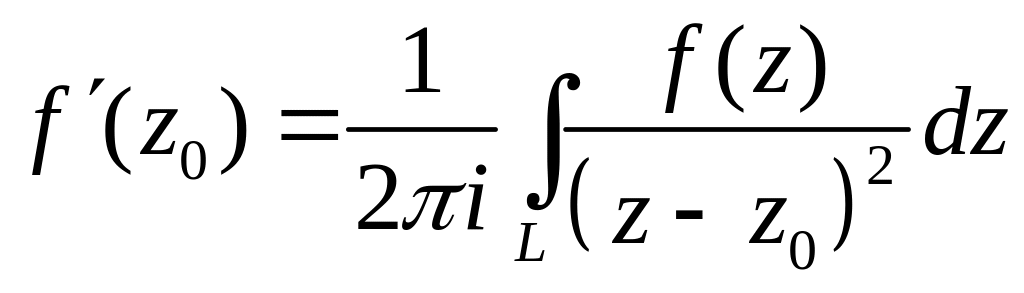 ,
значит, (7) справедлива для n=1.
,
значит, (7) справедлива для n=1.
Методом
математической индукции доказывается,
что (7) верно
![]() .
.
Замечание 1. Из (7) следует, что
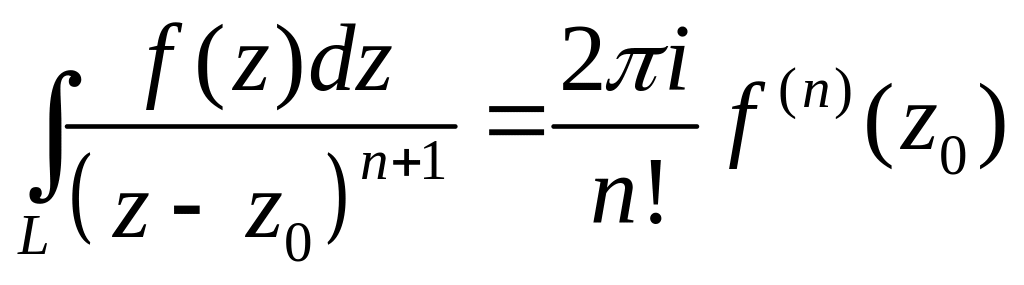 . (9)
. (9)
Замечание
2.
В теореме установлено, что если f(z)
имеет производную в любой
точке
z
из области D,
то она в каждой точке этой области имеет
производную любого порядка. Следовательно,
все производные аналитической функции
являются непрерывными. В частности,
если
f(z)
на D,
то она обязательно непрерывна. Для
действительной функции действительной
переменной это выполняется далеко не
всегда. Например,
![]() ,
,
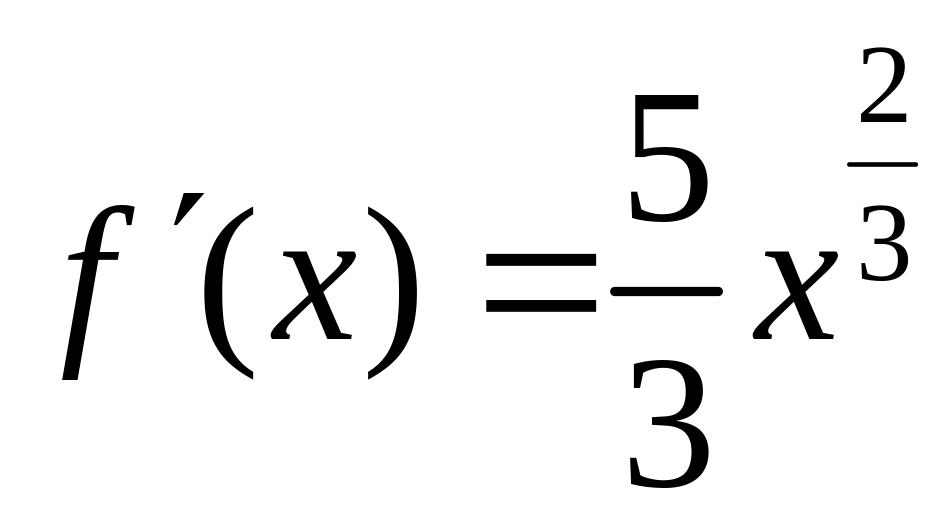 ,
f(x)
дифференцируема на
,
,
f(x)
дифференцируема на
,
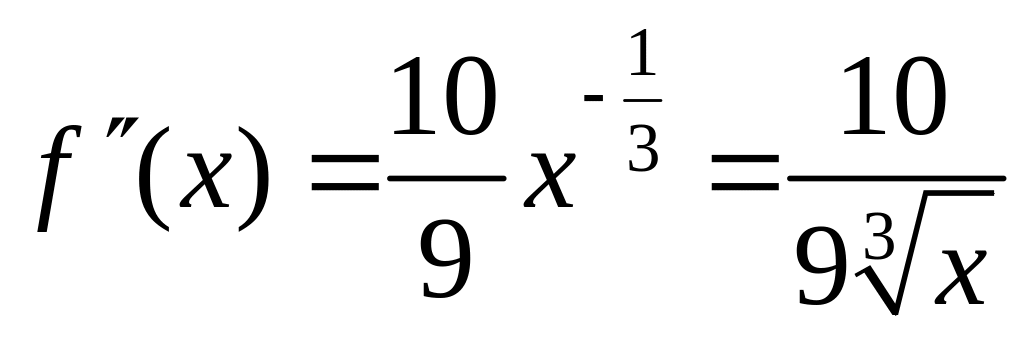 - не дифференцируема в точке x=0.
- не дифференцируема в точке x=0.
П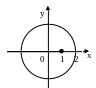 ример
1.
Вычислить
ример
1.
Вычислить
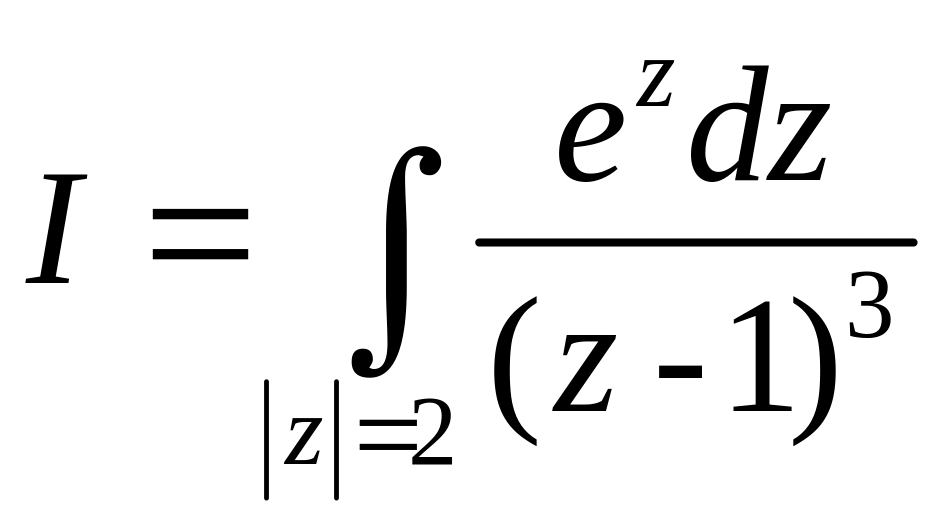
Δ f(z)=ez - аналитическая на , z0=1, n+1=3, следовательно, n=2. По формуле (9):
![]() .
Δ
.
Δ
Пример
2.
Вычислить
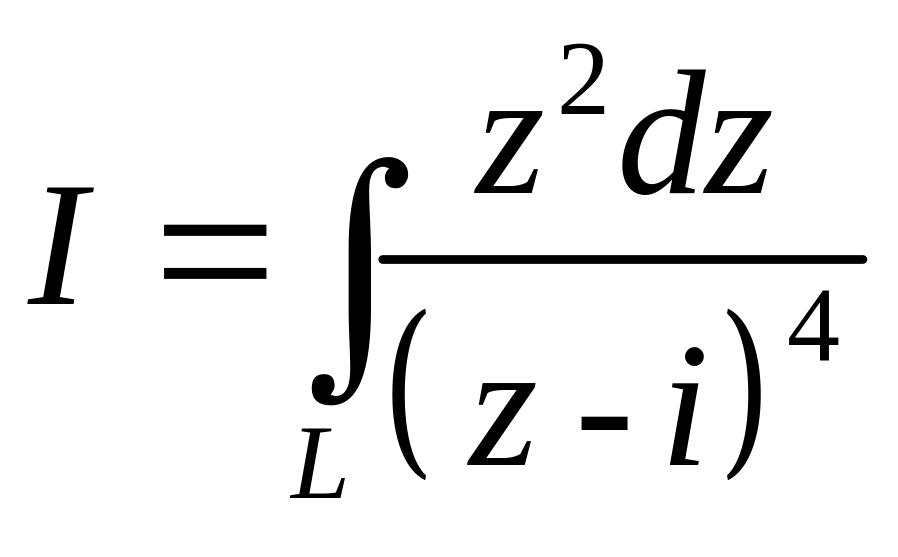 ,
где L
-
произвольный кусочно–гладкий замкнутый
контур.
,
где L
-
произвольный кусочно–гладкий замкнутый
контур.
Δ Рассмотрим 2 случая:
L- кусочно–гладкий замкнутый контур, такой что z=i лежит внутри L;
z=i лежит вне контура L.
а)
f(z)=z
2-
аналитическая на
,
z0=i,
n=3.
Следовательно,
![]() .
.
f (z)=2z, f (z)=2, f (z)=0. Следовательно, I=0.
b) I=0 на основании интегральной теоремы Коши.
Из a),
b)
следует что
 по любому кусочно–гладкому замкнутому
контуру, такому, что iL.
Δ
по любому кусочно–гладкому замкнутому
контуру, такому, что iL.
Δ
