
- •§1. Комплексные числа и действия над ними
- •1.Понятие комплексного числа. Действия над комплексными числами
- •2. Геометрическая интерпретация комплексного числа.
- •3. Комплексная плоскость как метрическое пространство
- •§2.Последовательности комплексных чисел. Предел последовательности
- •§3. Расширенная комплексная плоскость
- •§4. Функции комплексного переменного
- •1. Комплексно-значные функции действительной переменной
- •2. Кривые на комплексной плоскости
- •3.Функции комплексного переменного
- •§5. Предел и непрерывность функции комплексного переменного
- •1. Предел функции комплексного переменного
- •2.Непрерывность функции комплексного переменного
- •§6. Геометрическая интерпретация функции комплексного переменного
- •§7.Дифференцирование функции одной комплексной переменной
- •1.Производная функции комплексной переменной
- •2. Необходимые и достаточные условия
- •3. Понятие аналитической функции
- •4. Гармонические функции
- •5. Восстановление аналитической функции
- •6. Геометрический смысл аргумента и модуля производной
- •7. Понятие о конформном отображении
- •§8. Простейшие элементарные функции комплексной переменной
- •1. Линейная функция
- •2. Дробно-линейная функция
- •3.Многочлен
- •4. Показательная функция
- •5. Тригонометрические функции
- •6. Гиперболические функции
- •7. Области однолистности аналитических функций. Обратные функции
- •8. Степенная функция и радикал
- •9. Логарифмическая функция
- •10. Общие степенная и показательная функции
- •§9. Интегрирование функций комплексного переменного
- •1.Понятие интеграла
- •2.Вычисление интеграла от функции комплексного переменного
- •3.Основные свойства интеграла от функции комплексного переменного
- •§10. Интегральная теорема Коши
- •§11. Первообразная
- •§12. Интегральная формула Коши и ее следствия
- •1. Интегральная формула Коши
- •2. Бесконечная дифференцируемость аналитической функции
- •3. Теорема Морера
- •4. Теорема о среднем
- •5. Принцип максимума модуля аналитической функции
§11. Первообразная
Если
f(z)
аналитическая в односвязной области
D
функция, то, как было установлено,
значение
,
взятого по любой кусочно – гладкой
кривой LD,
не зависит от вида кривой, а определяется
лишь начальной и конечной точками
кривой. Поэтому для интеграла вдоль
произвольной кусочно – гладкой кривой
L,
соединяющей точки z0
и z,
используют обозначение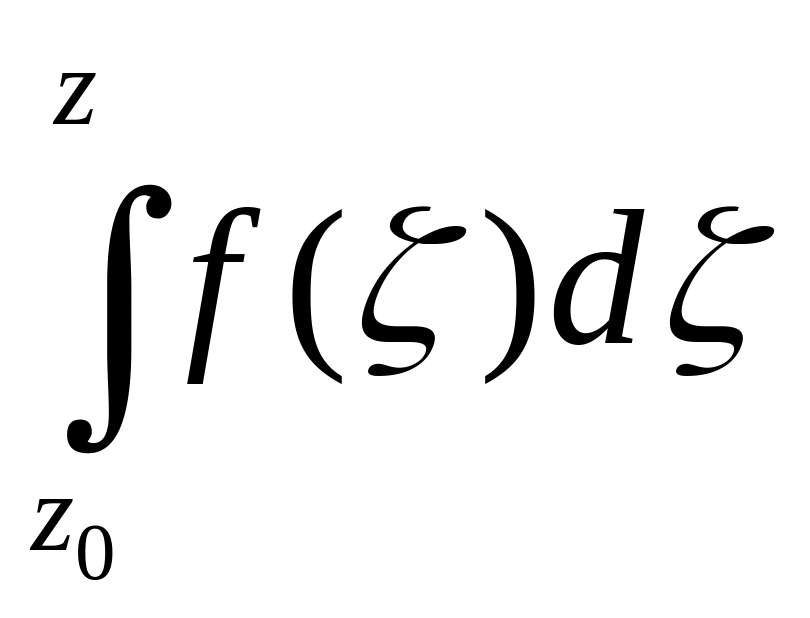 ,
где z0
и z
называются соответственно, нижним и
верхним пределами интегрирования.
,
где z0
и z
называются соответственно, нижним и
верхним пределами интегрирования.
Зафиксируем
z0,
тогда
зависит только от точки z,
т.е. является однозначной функцией,
определённой на D,
т.е.
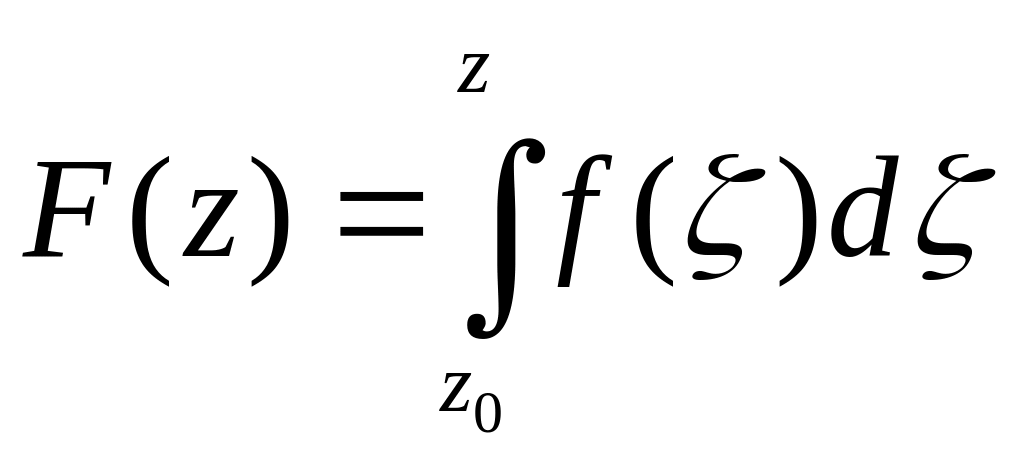 .
.
Теорема
1.
Пусть f(z)-функция,
непрерывная в области D,
для которой интеграл
вдоль любой кусочно – гладкой кривой
LD
не
зависит от вида кривой, а определяется
только начальной и конечной точками
кривой. Тогда
является аналитической на D
функцией и F'(z)=f(z)
![]() .
.
Доказательство.
Пусть L D-кусочно-гладкая кривая, соединяющая точки z0 и z. Выберем ∆z≠0 так, чтобы z+∆z D.
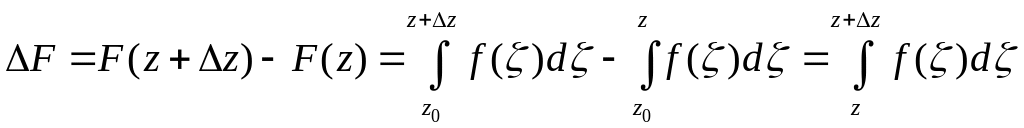 .
.
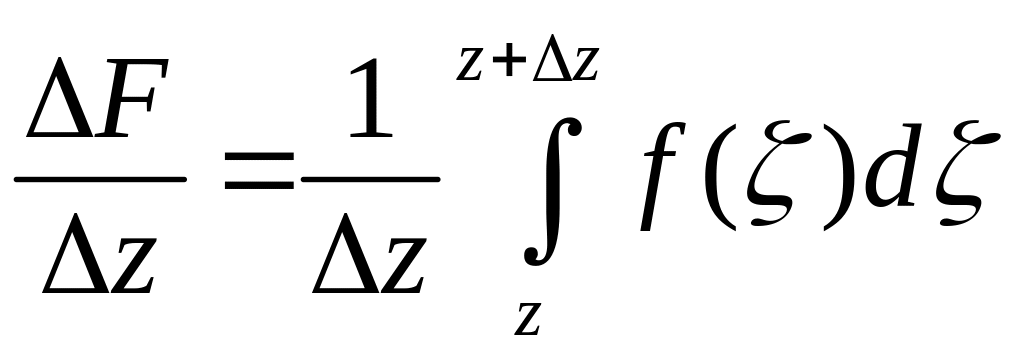
 . (1)
. (1)
Т.к.
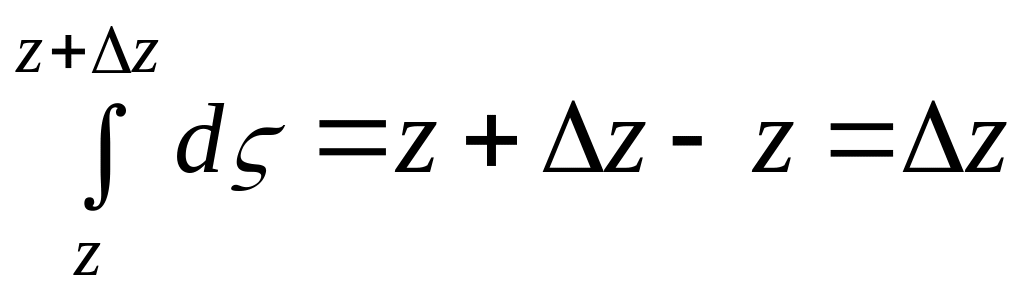 ,
то
,
то
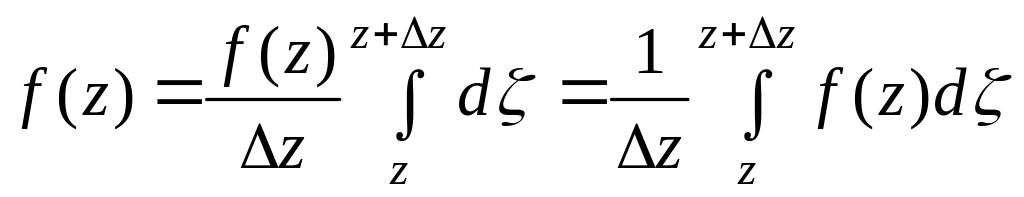 . (2)
. (2)
Интегралы (1) и (2) не зависят от пути интегрирования, поэтому в качестве пути от z до z+∆z можно взять прямолинейный отрезок, соединяющий эти точки. Из (1) и (2) следует:
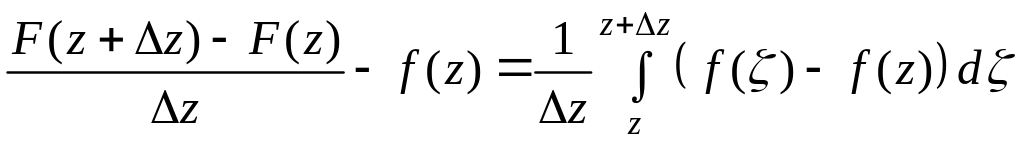 . (3)
. (3)
Зафиксируем >0. Так как f(z) непрерывна на D, то для любой точки z D выполнено
![]()
![]() . (4)
. (4)
В
равенстве (3)
![]() .
Следовательно,
.
Следовательно,
![]()
![]() .
Поэтому если
.
Поэтому если
![]() ,
то
,
то
![]() ,
значит, выполнено
(4).
,
значит, выполнено
(4).
Тогда из (3) следует
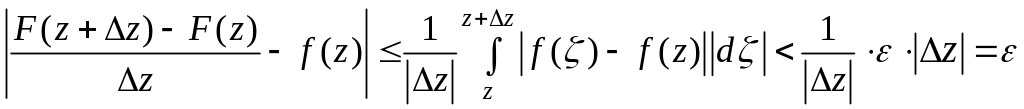
![]() .
.
Таким
образом,
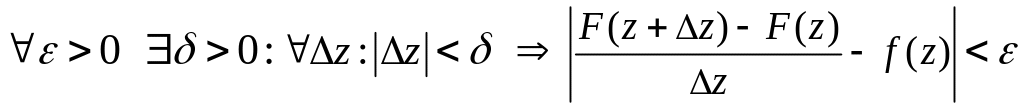 .
.
По
определению это означает, что
![]() ,
,
то есть F'(z)=f(z) .
Замечание 1. Теорему 1 можно было сформулировать следующим образом:
если
f(z)
аналитическая в области D
функция, то
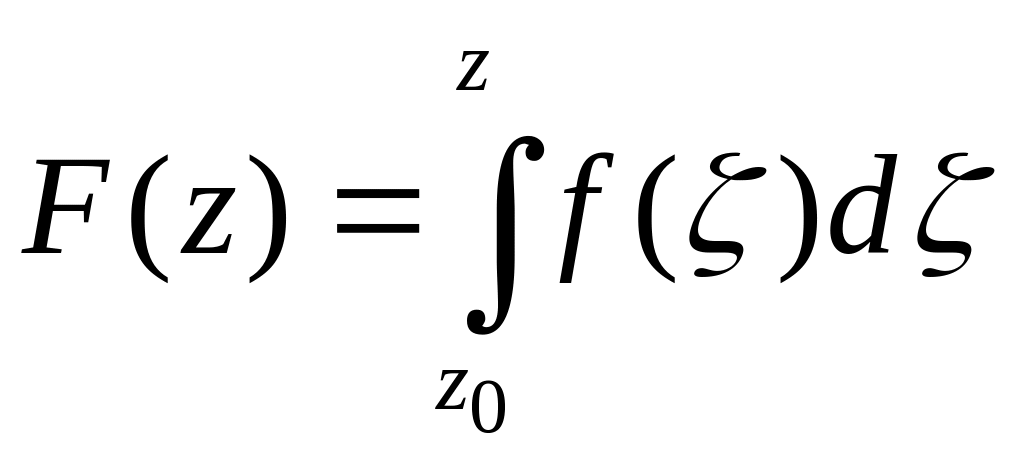 - аналитическая функция и F'(z)=f(z),
где интеграл берётся по любой
кусочно-гладкой кривой, соединяющей
точки z0
и z.
- аналитическая функция и F'(z)=f(z),
где интеграл берётся по любой
кусочно-гладкой кривой, соединяющей
точки z0
и z.
Действительно,
если f(z)
– аналитическая функция, то
![]() не
зависит от пути интегрирования.
не
зависит от пути интегрирования.
Определение. Функция F(z) называется первообразной для функции f(z) на области G, если F'(z)=f(z) .
Из
определения следует, что если F(z)
первообразная для f(z)
на D,
то и функция F(z)+C
является первообразной для f(z)
на D
(![]() ).
).
Следовательно, если выполнены условия теоремы 1, то функция f(z) имеет первообразную.
Теорема 2. Если f(z)-аналитическая на односвязной области D, и F(z), (z)-две первообразные для f(z) на D, то справедливо F(z)-Φ(z)=С=const.
Доказательство.
Пусть F(z) и Φ(z) - две первообразные функции f(z) на D. Рассмотрим функцию w(z)=F(z)-Φ(z) , w(z)=u(x,y)+iv(x,y).
Тогда w(z)=F'(z)-Φ'(z)=f(z)-f(z)=0 .
Так
как
![]() ,
то
,
то
![]() и
и
![]() .
.
Так
как w(z)
- аналитическая
функция, то
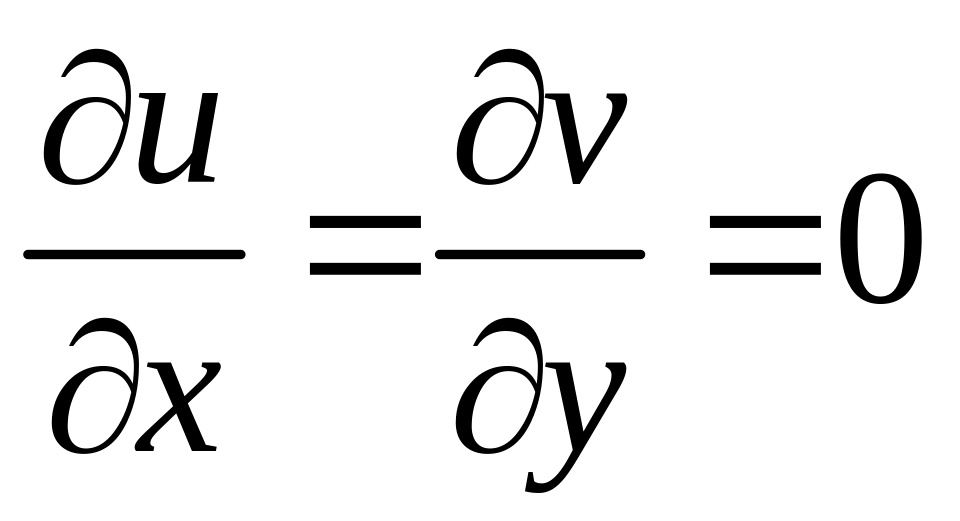 и
и
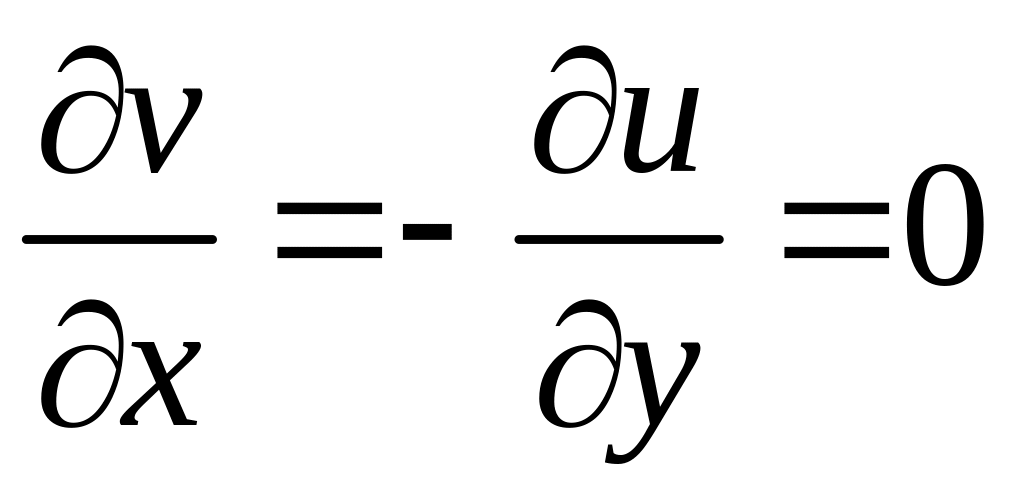 .
.
Итак,
,
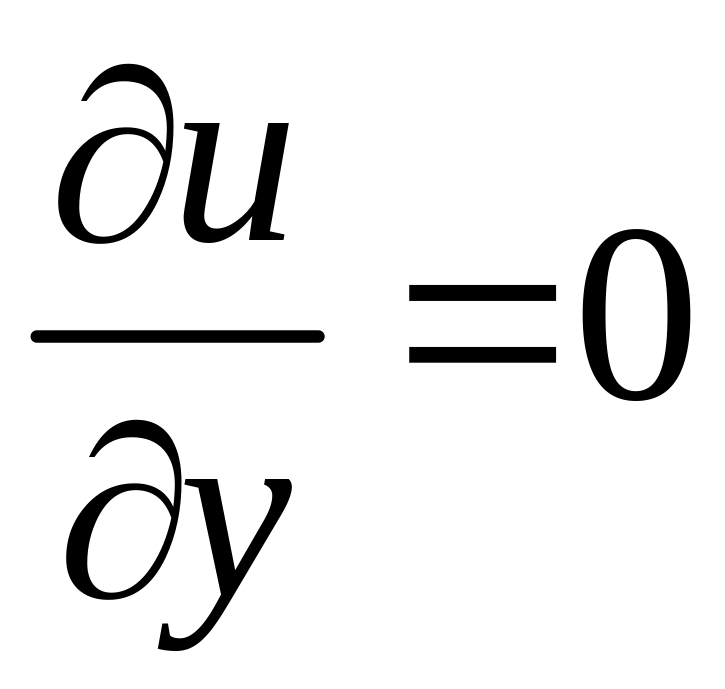
u=aconst,
u=aconst,
,
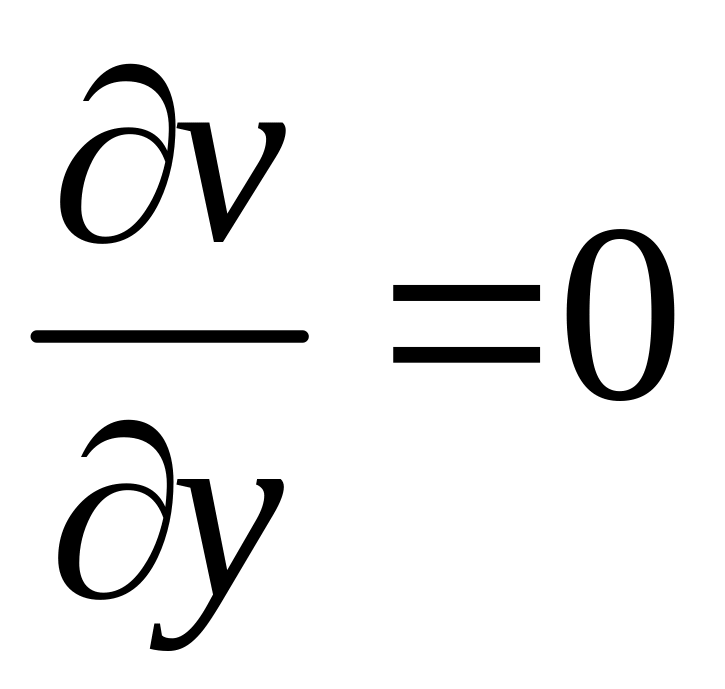
v=bconst.
v=bconst.
Тогда w(z)=a+ibconst.
Значит, F(z)-Φ(z)=С.
Следствие 1. Если f(z)-аналитическая на односвязной области D, то любая её первообразная имеет вид
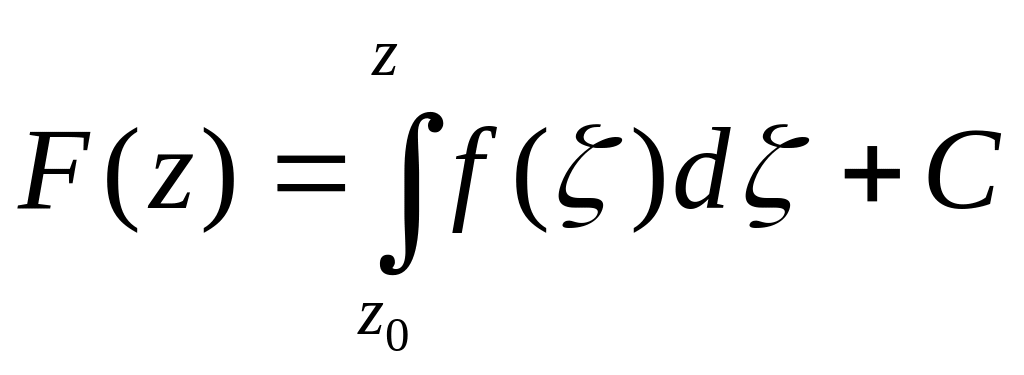 ,
где
,
где
![]() . (5)
. (5)
Следствие 2. Положим в (5) z=z0, тогда C=F(z0).Заменяя в (5) C на F(z0) получим:
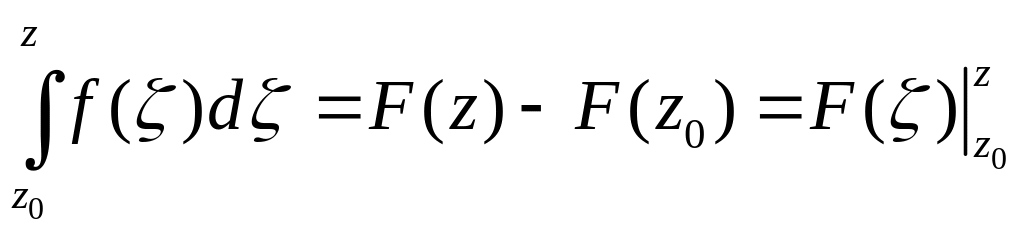 -
формула Ньютона-Лейбница.
-
формула Ньютона-Лейбница.
Таким образом, интеграл от аналитической функции комплексной переменной вычисляется с помощью тех же методов и формул, что и в случае функции действительной переменной.
Пример
1. Вычислить
![]() ,
где L–дуга
окружности |z|=2
от точки z1=2
до точки z2=2i.
,
где L–дуга
окружности |z|=2
от точки z1=2
до точки z2=2i.
f(z)=z2
– аналитическая в
![]() ,
,
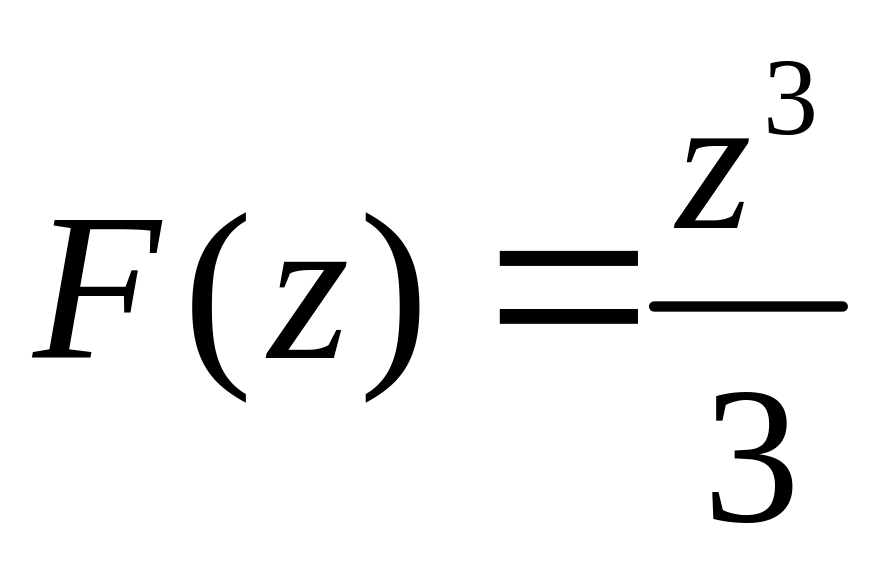 на
.
Следовательно, по формуле Ньютона-Лейбница:
на
.
Следовательно, по формуле Ньютона-Лейбница:
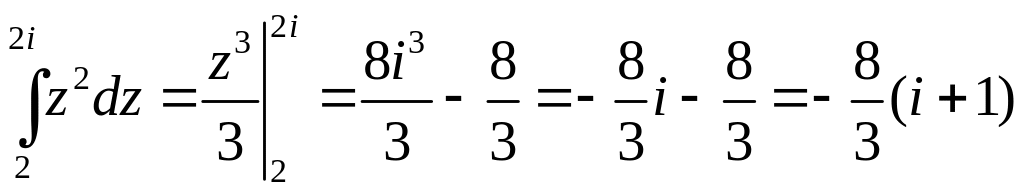 .
.
Пример
2. 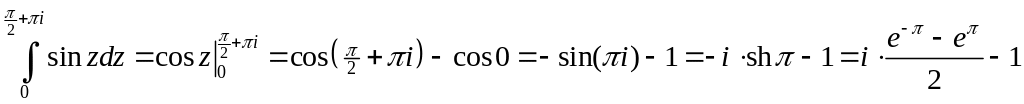 .
.
