
- •§1. Комплексные числа и действия над ними
- •1.Понятие комплексного числа. Действия над комплексными числами
- •2. Геометрическая интерпретация комплексного числа.
- •3. Комплексная плоскость как метрическое пространство
- •§2.Последовательности комплексных чисел. Предел последовательности
- •§3. Расширенная комплексная плоскость
- •§4. Функции комплексного переменного
- •1. Комплексно-значные функции действительной переменной
- •2. Кривые на комплексной плоскости
- •3.Функции комплексного переменного
- •§5. Предел и непрерывность функции комплексного переменного
- •1. Предел функции комплексного переменного
- •2.Непрерывность функции комплексного переменного
- •§6. Геометрическая интерпретация функции комплексного переменного
- •§7.Дифференцирование функции одной комплексной переменной
- •1.Производная функции комплексной переменной
- •2. Необходимые и достаточные условия
- •3. Понятие аналитической функции
- •4. Гармонические функции
- •5. Восстановление аналитической функции
- •6. Геометрический смысл аргумента и модуля производной
- •7. Понятие о конформном отображении
- •§8. Простейшие элементарные функции комплексной переменной
- •1. Линейная функция
- •2. Дробно-линейная функция
- •3.Многочлен
- •4. Показательная функция
- •5. Тригонометрические функции
- •6. Гиперболические функции
- •7. Области однолистности аналитических функций. Обратные функции
- •8. Степенная функция и радикал
- •9. Логарифмическая функция
- •10. Общие степенная и показательная функции
- •§9. Интегрирование функций комплексного переменного
- •1.Понятие интеграла
- •2.Вычисление интеграла от функции комплексного переменного
- •3.Основные свойства интеграла от функции комплексного переменного
- •§10. Интегральная теорема Коши
- •§11. Первообразная
- •§12. Интегральная формула Коши и ее следствия
- •1. Интегральная формула Коши
- •2. Бесконечная дифференцируемость аналитической функции
- •3. Теорема Морера
- •4. Теорема о среднем
- •5. Принцип максимума модуля аналитической функции
3.Основные свойства интеграла от функции комплексного переменного
Все кривые являются простыми и гладкими.
1 Линейность интеграла
![]() .
.
2 Аддитивность
Если
![]() (
где
(
где
![]() и
и
![]() не имеют общих точек за исключением
начала
и конца
),
то
не имеют общих точек за исключением
начала
и конца
),
то
![]() .
.
3![]() ,
где
,
где
![]() -
кривая L,
пройденная в противоположном направлении.
-
кривая L,
пройденная в противоположном направлении.
Доказательство свойств 1-3следует из определения интеграла и из свойств криволинейных интегралов II типа от функции действительной переменной.
4
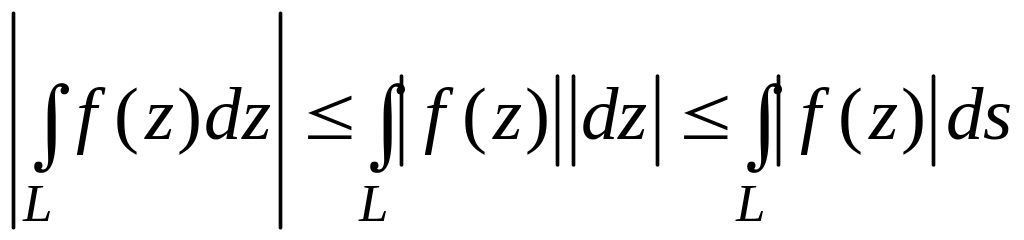 ,
где s
–длина дуги, отсчитываемая от начала
L
до произвольной точки в выбранном
направлении.
,
где s
–длина дуги, отсчитываемая от начала
L
до произвольной точки в выбранном
направлении.
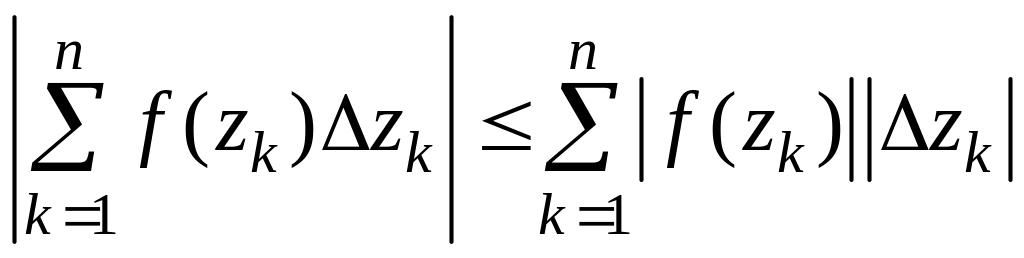 .
.
Т.к.
![]() -длина хорды, то
-длина хорды, то
![]() - где
- где
![]() длина дуги
длина дуги
![]() ,
следовательно,
,
следовательно,
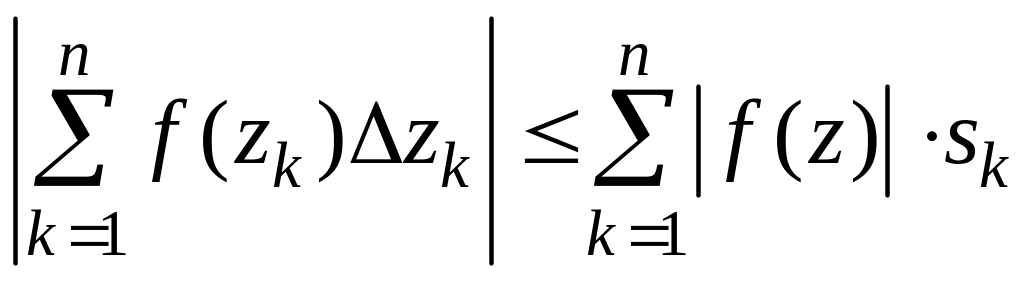 .
Переходя к пределу при
.
Переходя к пределу при
![]() ,
получим
,
получим
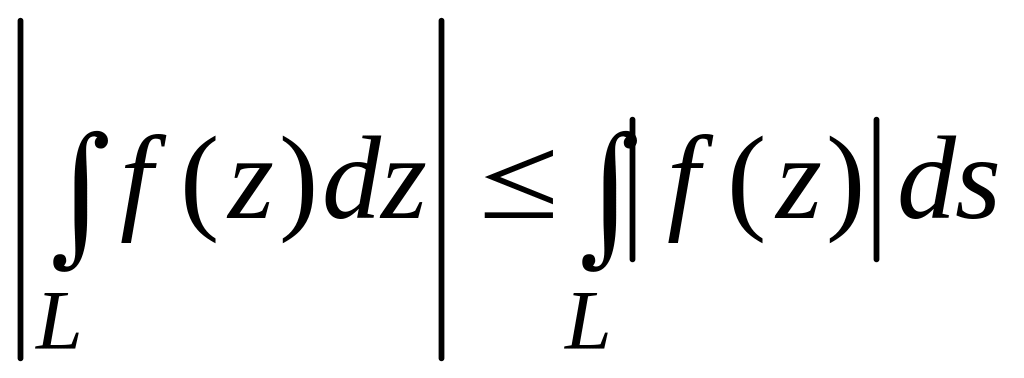 .
.
5
Если
![]() ,
то
,
то
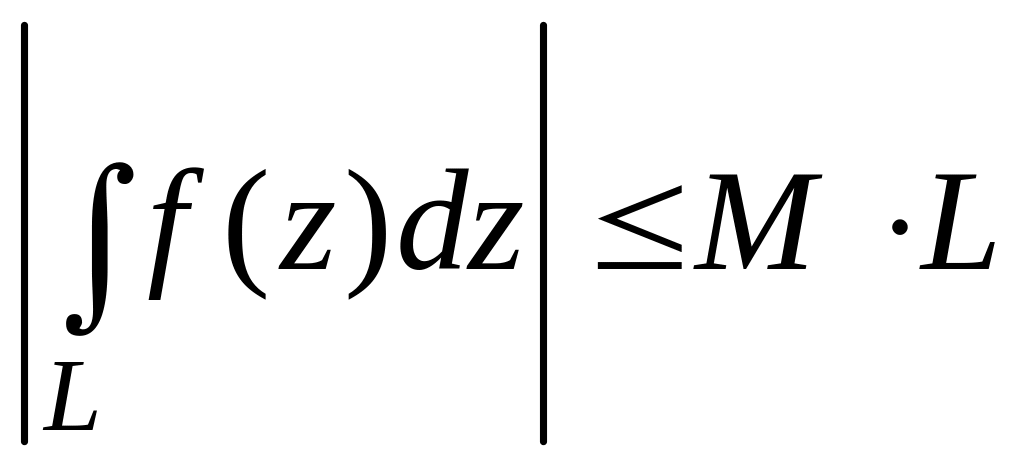 ,
где L
–длина кривой L.
,
где L
–длина кривой L.
5
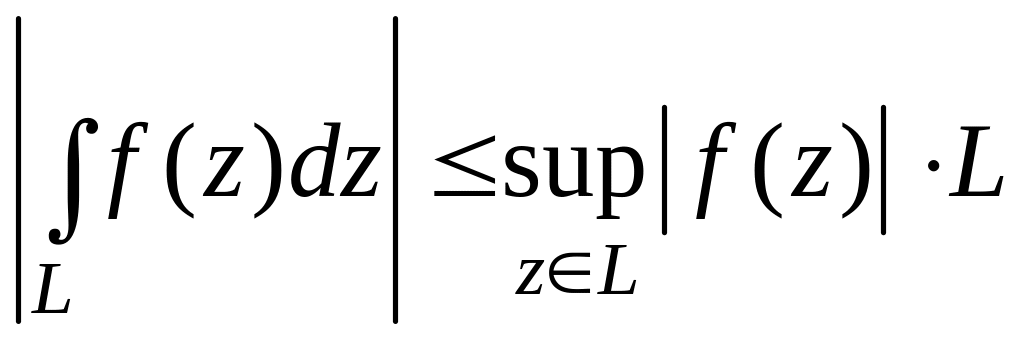 .
.
§10. Интегральная теорема Коши
Рассмотрим
![]() .
Он зависит от функции f(z)
и от вида кривой L.
Возникает вопрос: каким условиям должна
удовлетворять функция f(z),
чтобы интеграл не зависел от пути
интегрирования L,
а определялся начальной и конечной
точками кривой.
.
Он зависит от функции f(z)
и от вида кривой L.
Возникает вопрос: каким условиям должна
удовлетворять функция f(z),
чтобы интеграл не зависел от пути
интегрирования L,
а определялся начальной и конечной
точками кривой.
Как и в случае криволинейного интеграла II рода независимость интеграла от пути интегрирования равносильна равенству нулю этого интеграла по любому замкнутому контуру.
Теорема.
не
зависит от пути интегрирования на
области D
тогда и только тогда, когда
![]() по любому кусочно-гладкому контуру
по любому кусочно-гладкому контуру
![]() .
.
Доказательство.
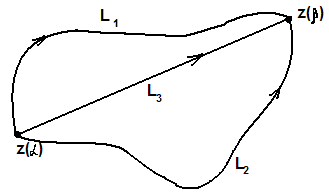
 (
(![]() )
Пусть
)
Пусть
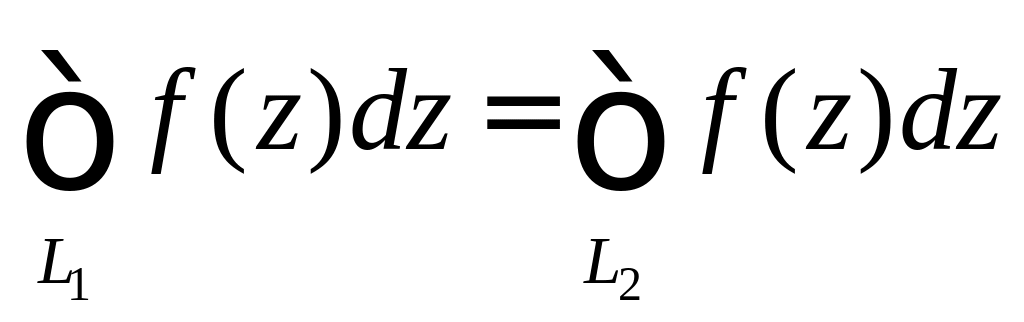 ,
где
,
где
![]() и
и
![]() -кривые,
лежащие в D
и соединяющие точки A
и B.
Тогда
-кривые,
лежащие в D
и соединяющие точки A
и B.
Тогда
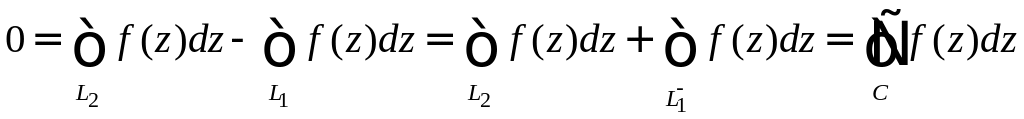 ,
где
,
где
![]() .
.
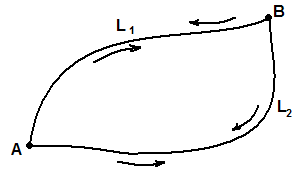
(![]() )
Пусть
,
где C
- кусочно-гладкий замкнутый контур,
.
Разобьем C
точками A
и B
на кривые
и
так, что
.
Тогда
)
Пусть
,
где C
- кусочно-гладкий замкнутый контур,
.
Разобьем C
точками A
и B
на кривые
и
так, что
.
Тогда
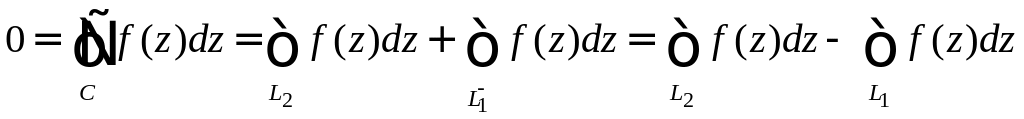
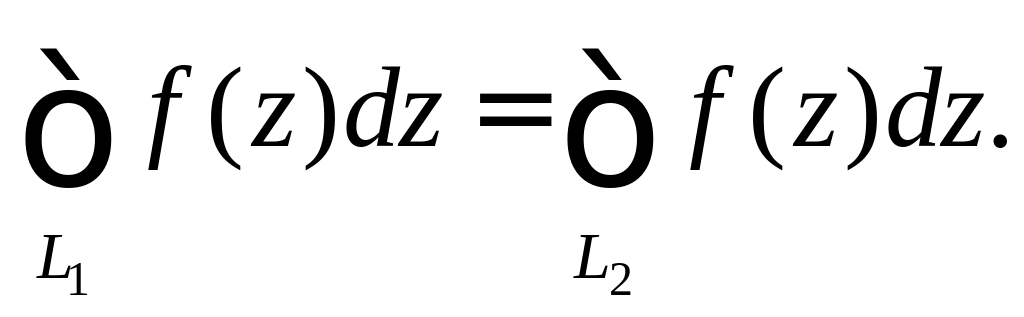
Для доказательства интегральной теоремы Коши нам понадобится следующая
Л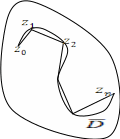 емма.
Пусть
f(z)-
непрерывная в области G
функция, L
- произвольная кусочно - гладкая линия,
LG.
Тогда >0
существует ломаная P,
вписанная в L,
PG,
такая что
емма.
Пусть
f(z)-
непрерывная в области G
функция, L
- произвольная кусочно - гладкая линия,
LG.
Тогда >0
существует ломаная P,
вписанная в L,
PG,
такая что
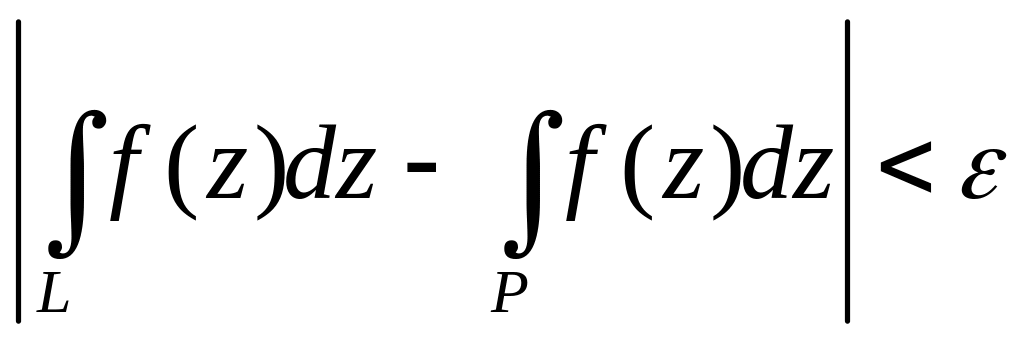 .
.
Доказательство.
![]() Разобьём
L
на частичные дуги
Разобьём
L
на частичные дуги
![]() ,
,
![]() ,…,
,…,
![]() sk
– длина
).
Впишем в L
ломаную P,
звенья которой стягивают дуги
.
Точки z0,
z1,…,zn
– вершины ломаной P.
Звенья ломаной (и их длины) обозначим
через lk
,
k=
sk
– длина
).
Впишем в L
ломаную P,
звенья которой стягивают дуги
.
Точки z0,
z1,…,zn
– вершины ломаной P.
Звенья ломаной (и их длины) обозначим
через lk
,
k=![]()
Рассмотрим сумму
S=f(z1)z1+f(z2)z2+…+f(zn)zn . (4)
S
является интегральной суммой для
интеграла
,
в которой в качестве точек k
взяты точки zk.
Так
как f(z)
– непрерывна в G,
а L
–
кусочно – гладкая линия, то
![]() (
),
т.е. >0
1>0:
T:
<1
(
),
т.е. >0
1>0:
T:
<1
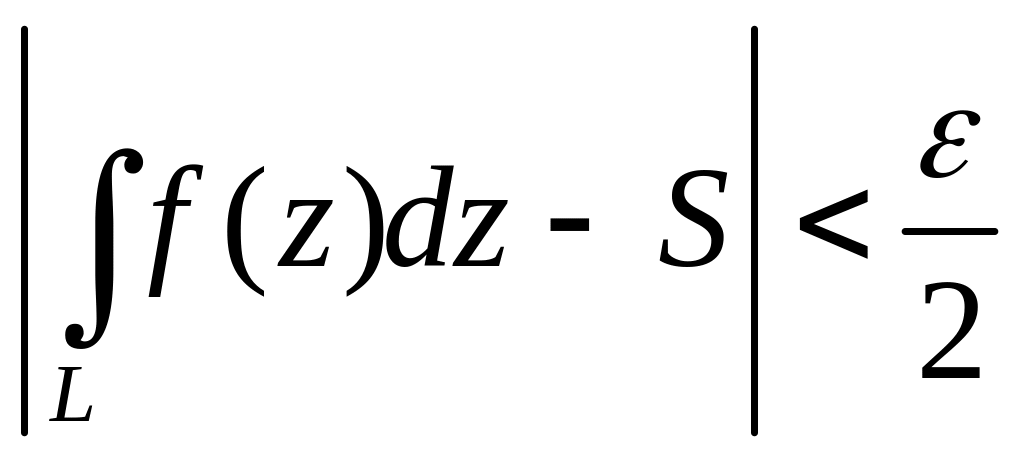 . (5),
. (5),
Оценим
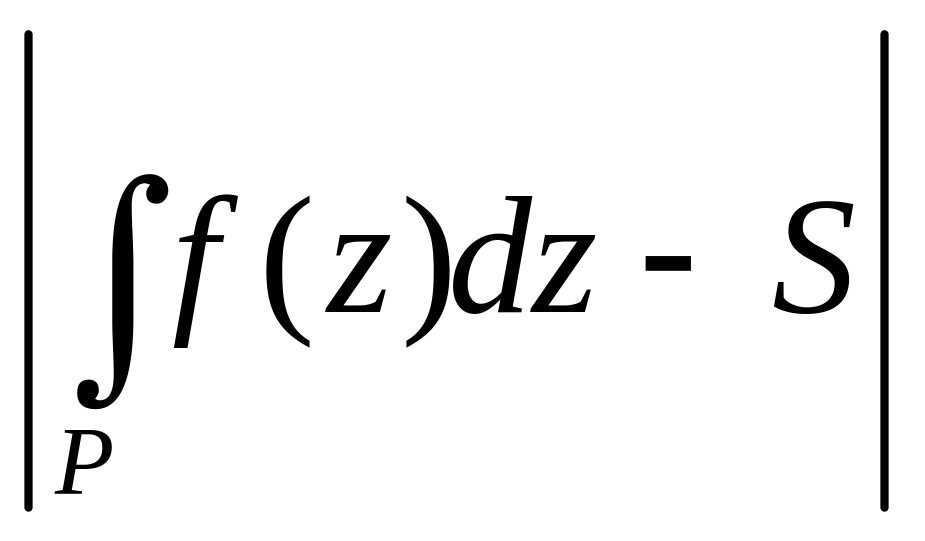 .
Так как
.
Так как
![]() ,
то (4) примет вид:
,
то (4) примет вид:
![]() .
(6)
.
(6)
С
другой стороны,
![]() . (7)
. (7)
Вычтем (6) из (7):
![]() .
.
Так как
функция f(z)
непрерывна
в G,
то она равномерно непрерывна на любом
ограниченном замкнутом множестве точек
из G.
Следовательно, она непрерывна на ломаной
P.
По определению равномерной непрерывности:
для выбранного числа >0
2>0:
z,
zP:
|z-z|<2
выполнено
![]() .
Пусть <2.
Так как k
на звене lk
|z-zk|<
lk<<2,
то
.
Пусть <2.
Так как k
на звене lk
|z-zk|<
lk<<2,
то
![]() .
Тогда
.
Тогда
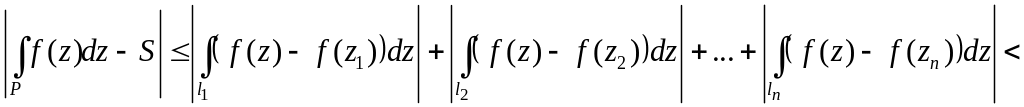
![]() .
(8)
.
(8)
Выберем =min{1;2}. Из (5) и (8) получим: >0 >0: T: < выполнено
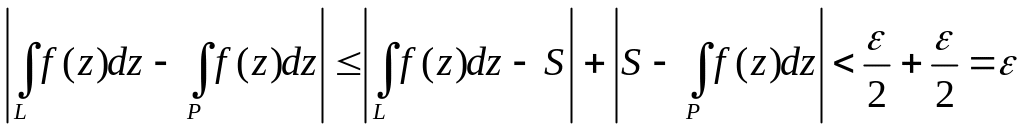 .
.
Итак,
в линию L
всегда можно вписать ломаную P
так, что разность значений
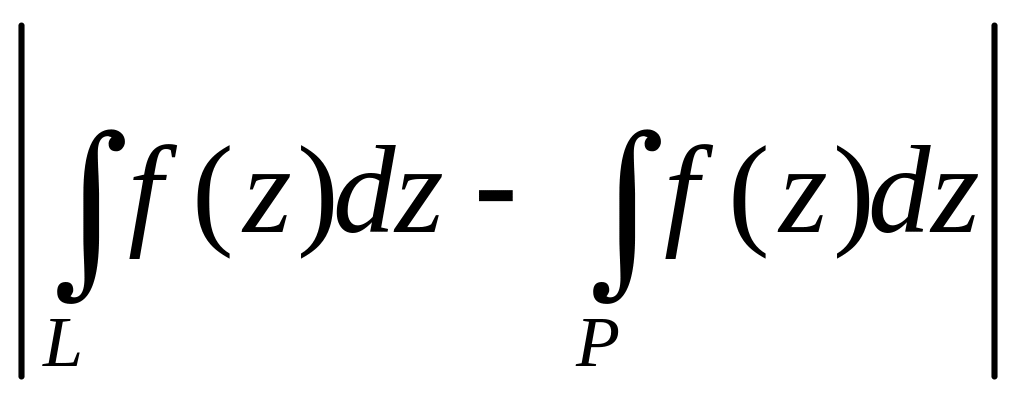 будет
меньше любого наперёд заданного числа.
будет
меньше любого наперёд заданного числа.
![]()
I. Случай односвязной области
Теорема
(Коши). Если
f(z)
аналитическая в односвязной области
G
функция, то![]() ,
где L-
любой замкнутый контур, лежащий в G.
,
где L-
любой замкнутый контур, лежащий в G.
Доказательство.
![]() Согласно
лемме в линию L
можно вписать ломаную P
так, что
Согласно
лемме в линию L
можно вписать ломаную P
так, что
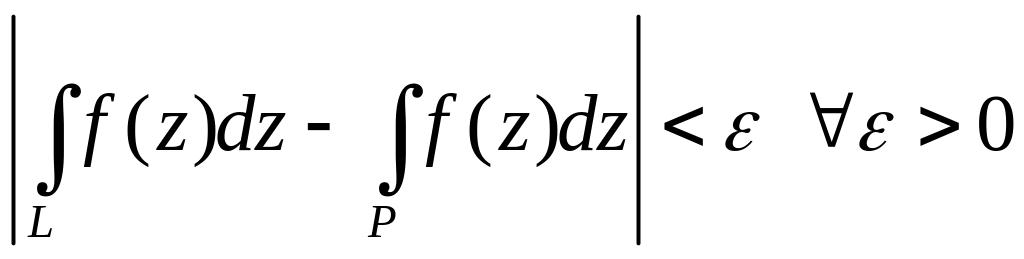 .
.
Следовательно,
если мы докажем, что
![]() ,
то отсюда будет следовать что
,
то отсюда будет следовать что
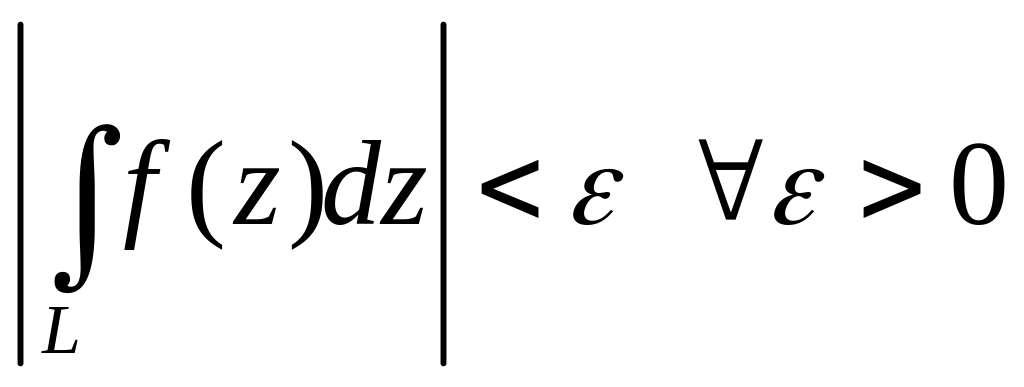 и, значит,
.
и, значит,
.
Следовательно, теорему достаточно доказать для случая, когда контуром интегрирования является ломаная P.
Далее:
данный многоугольник с периметром P
можно разбить на треугольники. Тогда
![]() ,
так как по AC,
DA
интегрирование совершается два раза
в противоположных направлениях.
Следовательно, если допустить, что
теорема Коши доказана для случая, когда
контуром интегрирования является любой
треугольник, то из последнего равенства
будет следовать, что
.
,
так как по AC,
DA
интегрирование совершается два раза
в противоположных направлениях.
Следовательно, если допустить, что
теорема Коши доказана для случая, когда
контуром интегрирования является любой
треугольник, то из последнего равенства
будет следовать, что
.
И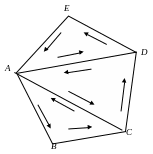 так,
докажем, что если f(z)
– аналитическая в области G
функция, то
так,
докажем, что если f(z)
– аналитическая в области G
функция, то![]() ,
где -
периметр любого треугольника, лежащего
в G.
,
где -
периметр любого треугольника, лежащего
в G.
Положим
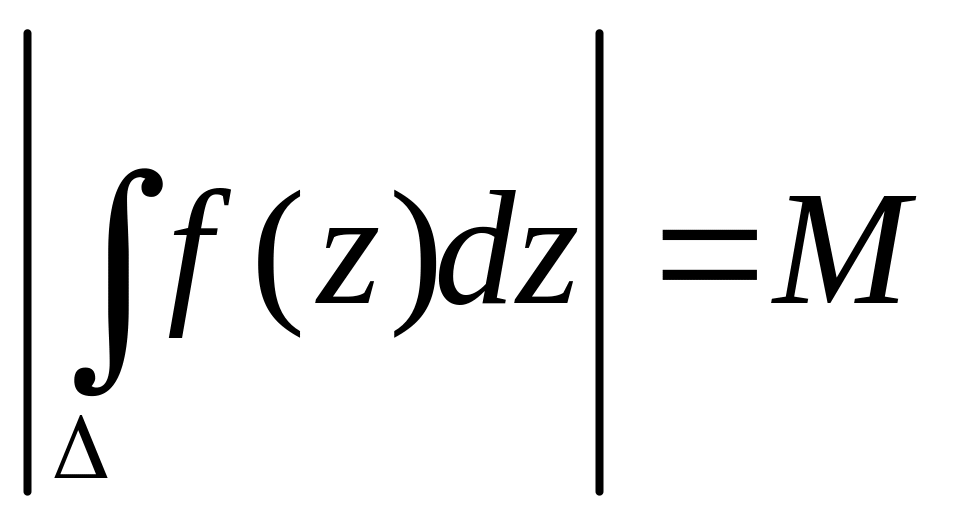 и докажем, что M=0.
и докажем, что M=0.
Р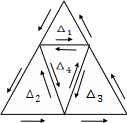 азделим
стороны треугольника пополам и соединим
точки деления. Треугольник, таким
образом, разобьётся на четыре равных
треугольника 1,
2,
3,
4.
азделим
стороны треугольника пополам и соединим
точки деления. Треугольник, таким
образом, разобьётся на четыре равных
треугольника 1,
2,
3,
4.
![]() .
.
Так как , то существует периметр k:
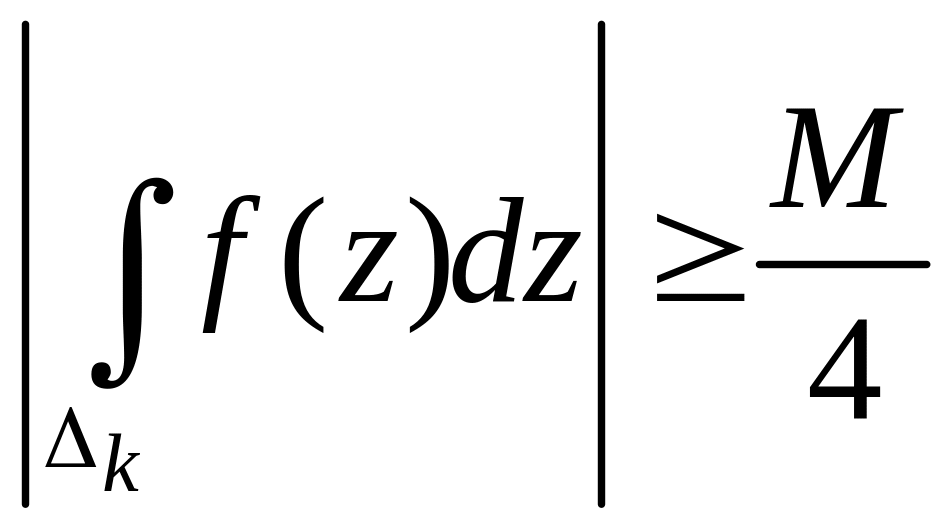 .
.
С этим
треугольником k=(1)
поступим так же, как и с ,
разбив на четыре разных треугольника.
Следовательно, существует треугольник
с периметром (2)(1):
 .
.
Этот процесс продолжим неограниченно, получим последовательность треугольников с периметрами =(0), (1), (2),…, (n),…, из которых каждый содержит следующий и таких, что:
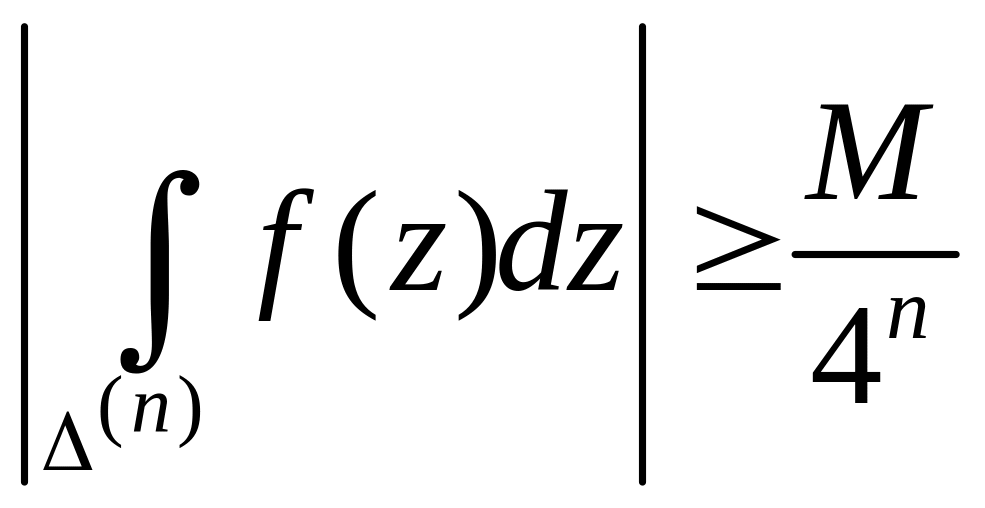 (n=0,1,…). (9)
(n=0,1,…). (9)
Обозначим
периметр
через U.
Тогда периметр
![]() .
.
Оценим
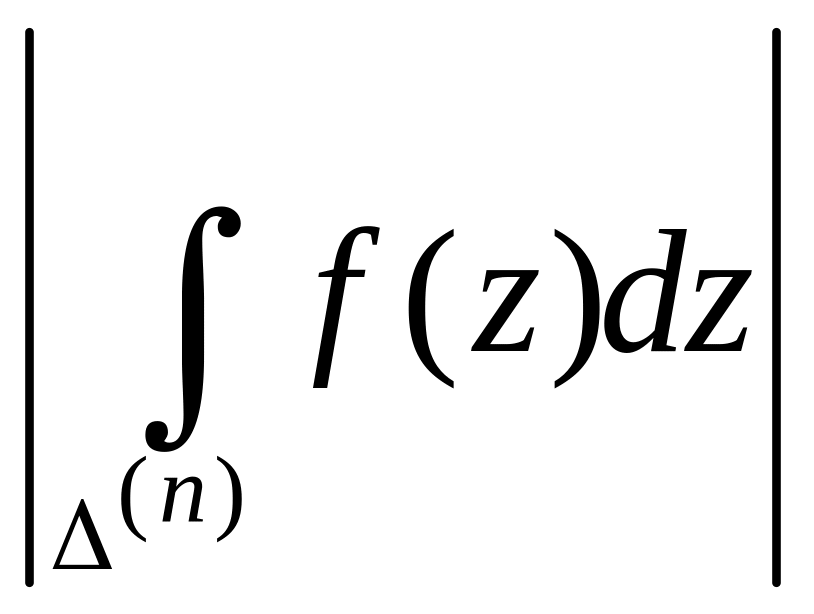 .
Имеем {(n)}
– последовательность вложенных
треугольников. Их периметры стремятся
к 0 при n.
Следовательно, существует точка z0,
принадлежащая всем треугольникам
последовательности {(n)}.
Так как z0G,
а f(z)-аналитическая
в G,
то
.
Имеем {(n)}
– последовательность вложенных
треугольников. Их периметры стремятся
к 0 при n.
Следовательно, существует точка z0,
принадлежащая всем треугольникам
последовательности {(n)}.
Так как z0G,
а f(z)-аналитическая
в G,
то
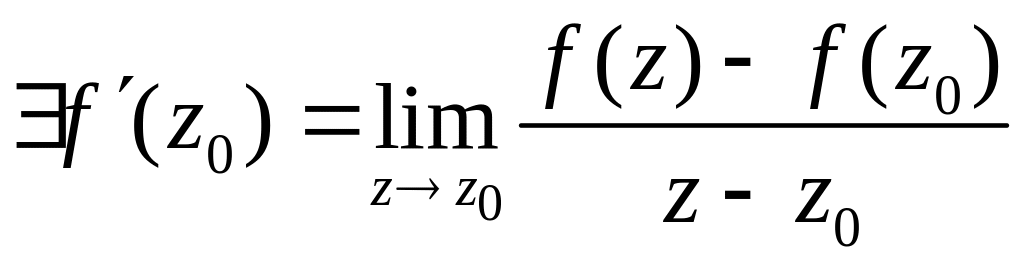 .
Следовательно, >0
()>0:
z:
|z-z0|<
выполнено
.
Следовательно, >0
()>0:
z:
|z-z0|<
выполнено
 ,
отсюда
,
отсюда
![]() . (10)
. (10)
Начиная
с достаточно большого номера n0,
треугольник (n)
будет находиться в круге
![]() и, следовательно, для оценки
можно использовать (10). Заметим,
что
и, следовательно, для оценки
можно использовать (10). Заметим,
что
![]()
![]() ,
,
так
как
![]() и
и
![]() (см.
пример о
(см.
пример о
![]() ).
).
Тогда
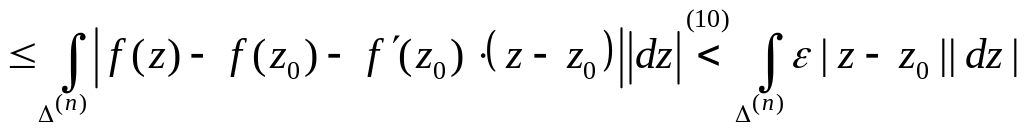 .
.
Так
как z0(n),
то
![]() (расстояние между z
и z0
меньше периметра).
(расстояние между z
и z0
меньше периметра).
Следовательно,
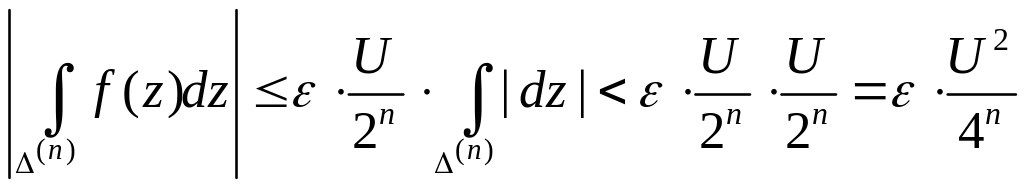 . (11)
. (11)
Из (9) и
(11) следует
![]() .
Так как -
произвольное сколь угодно малое число,
то переходя к пределу при 0,
получим M=0.
Следовательно,
.
.
Так как -
произвольное сколь угодно малое число,
то переходя к пределу при 0,
получим M=0.
Следовательно,
.
![]()
II. Случай многосвязной области
Пусть
D-
многосвязная область, граница которой
L
состоит из внешнего контура L0
и внутренних L1,
L2,…
Ln,
![]() ,
(D-
(n+1)-связная
область).
,
(D-
(n+1)-связная
область).
Определение. Положительным обходом границы L многосвязной области D называется такое направление обхода каждого контура, при котором область D остаётся всё время слева.
Теорема
(Коши). Пусть
f(z)
– аналитическая в области G,
D
– многосвязная область, которая вместе
со своей границей L
целиком лежит в G.
Т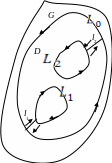 огда
,
где интеграл берётся в положительном
направлении.
огда
,
где интеграл берётся в положительном
направлении.
Доказательство.
Рассмотрим
случай n=2:
![]() .
Соединим контуры L1
и L2
c
внешним контуром L0
линиями l1,
l2
(l1
и l2
выберем
так, чтобы они не пересекались). Т.о., мы
получим односвязную область D*,
которая ограничена кривыми
L0,
L1,
L2,
l1,
l2,
причём
l1,
l2
проходятся
дважды в противоположных направлениях.
.
Соединим контуры L1
и L2
c
внешним контуром L0
линиями l1,
l2
(l1
и l2
выберем
так, чтобы они не пересекались). Т.о., мы
получим односвязную область D*,
которая ограничена кривыми
L0,
L1,
L2,
l1,
l2,
причём
l1,
l2
проходятся
дважды в противоположных направлениях.
![]() .
– граница D*.
По предыдущей теореме
.
– граница D*.
По предыдущей теореме
![]() Пользуясь свойством аддитивности
интеграла получим:
Пользуясь свойством аддитивности
интеграла получим:
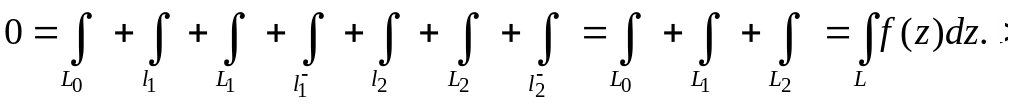
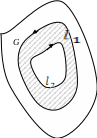 Следствие.
Если l1
и l2
кусочно – гладкие замкнутые кривые
ограничивающие кольцеобразную область
в области G,
и функция f(z)
– аналитическая в G,
то
Следствие.
Если l1
и l2
кусочно – гладкие замкнутые кривые
ограничивающие кольцеобразную область
в области G,
и функция f(z)
– аналитическая в G,
то![]() .
.
Пример
1.
![]() по
любому кусочно- гладкому замкнутому
контуру, так как f(z)=z3-3z
- аналитическая в
.
по
любому кусочно- гладкому замкнутому
контуру, так как f(z)=z3-3z
- аналитическая в
.
П ример
2.
ример
2.
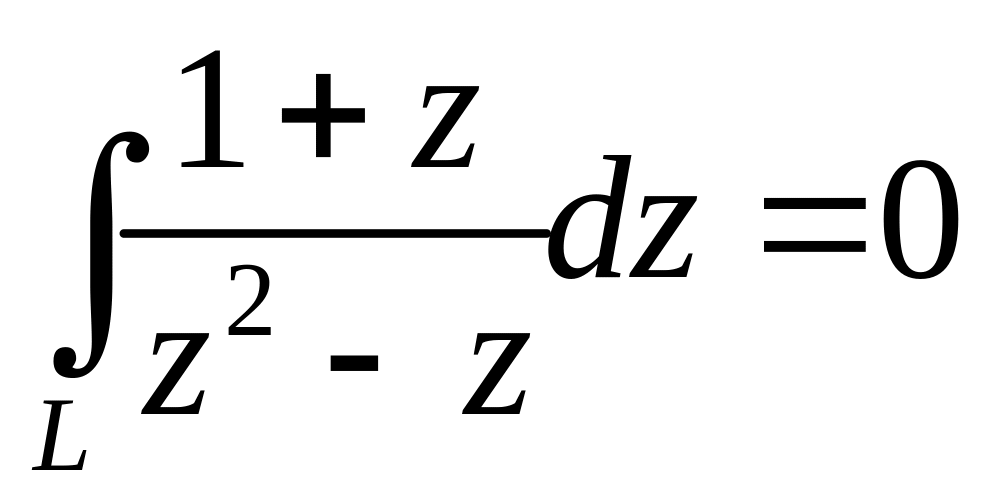 ,
если L
ограничивает область, не содержащую
точек z=0
и z=1.
,
если L
ограничивает область, не содержащую
точек z=0
и z=1.
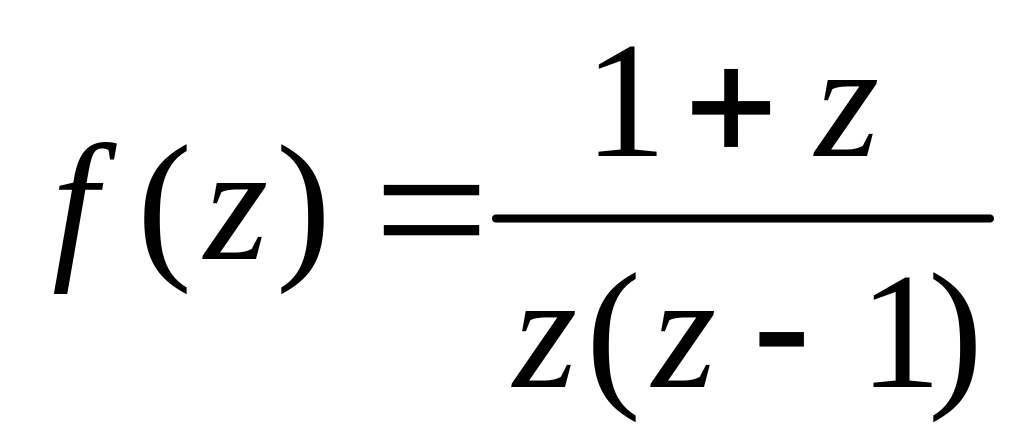 -
аналитическая в
-
аналитическая в
![]() .
Поэтому если L=L1={z:|z+2|<1},
то
.
А если
.
Поэтому если L=L1={z:|z+2|<1},
то
.
А если
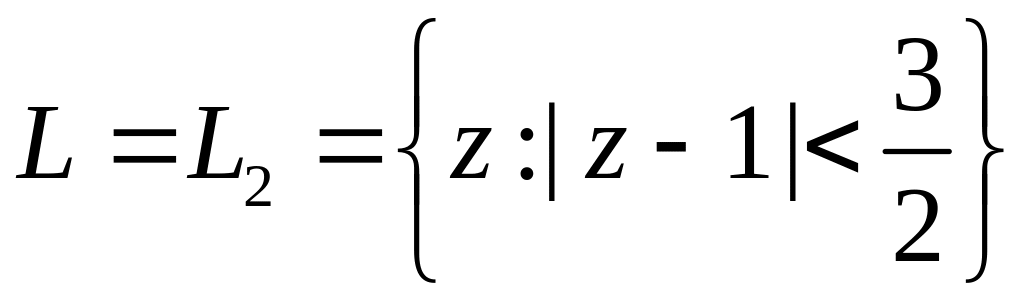 или
или
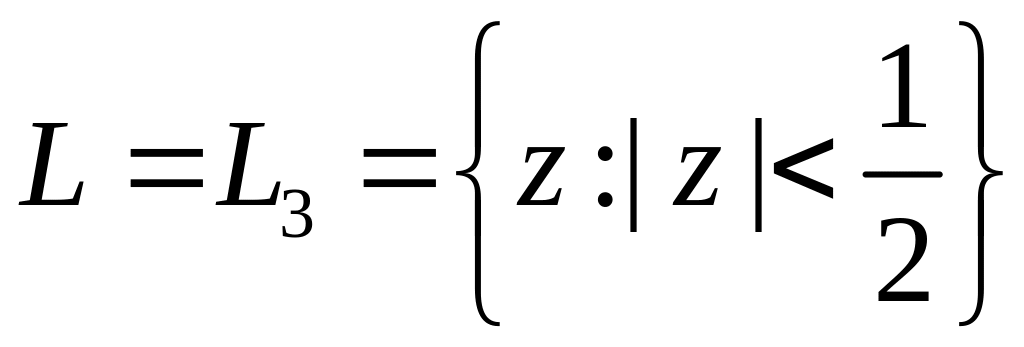 ,
то теорему Коши применять нельзя.
,
то теорему Коши применять нельзя.
П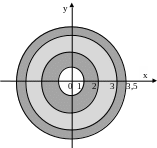 ример
3.
Даны два интеграла
ример
3.
Даны два интеграла
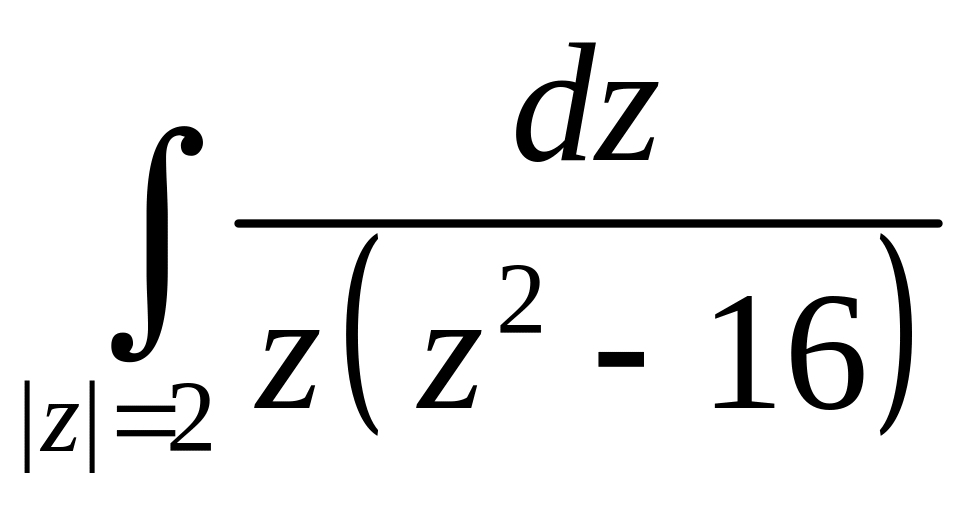 и
и
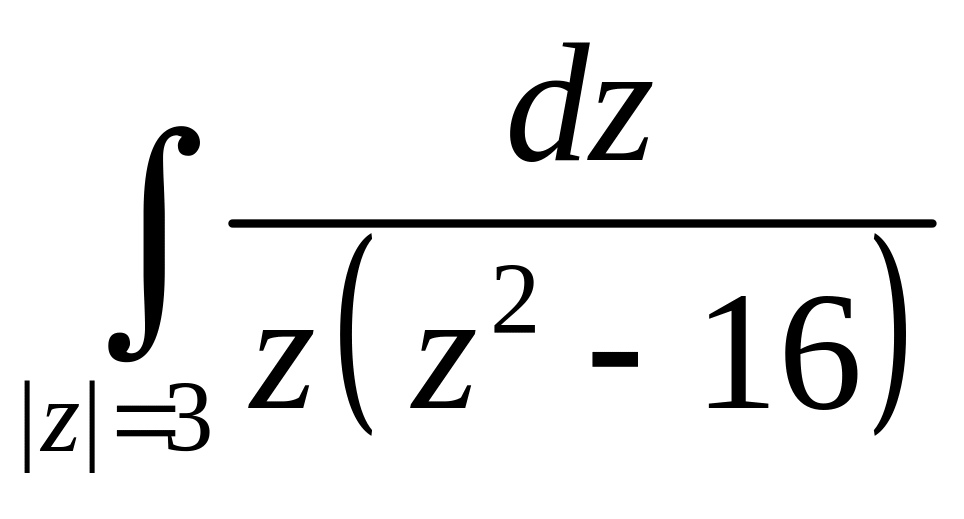 .
Равны ли они?
.
Равны ли они?
Применим
следствие. Рассмотрим область
![]() .
.
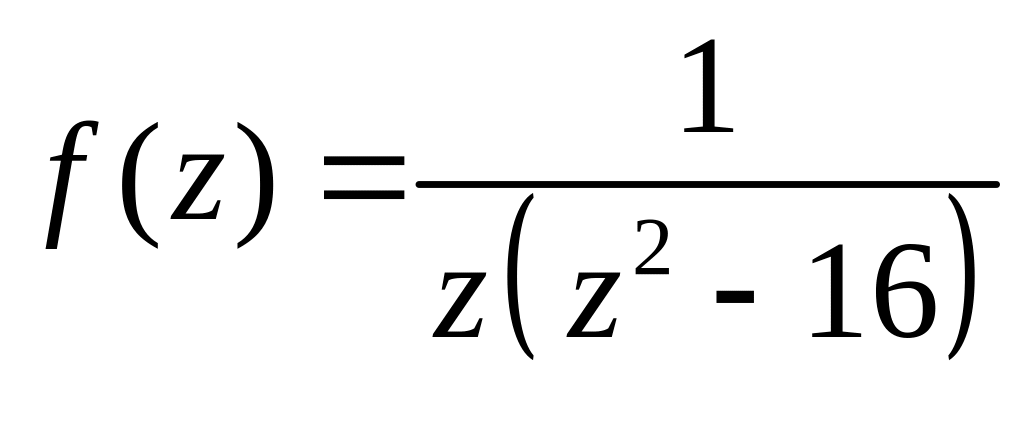 - аналитическая
в D.
Окружности |z|=2
и |z|=3
ограничивают кольцеобразную область
в D.
Следовательно (по следствию)
- аналитическая
в D.
Окружности |z|=2
и |z|=3
ограничивают кольцеобразную область
в D.
Следовательно (по следствию)
 .
.
Пример
4.
Доказать, что
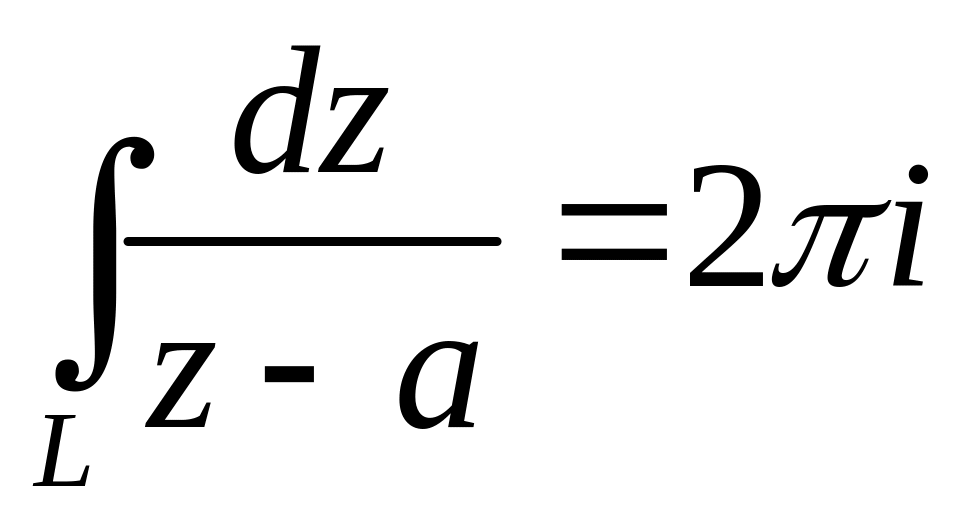 по любому кусочно –гладкому замкнутому
простому контуру, охватывающему (один
раз) точку a.
по любому кусочно –гладкому замкнутому
простому контуру, охватывающему (один
раз) точку a.
Пусть
C-окружность
с центром в точке а
радиуса r:
![]() ,
или C:
z=a+rei,
02,
d
,
или C:
z=a+rei,
02,
d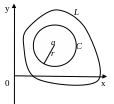 z=
ireid.
Тогда
z=
ireid.
Тогда
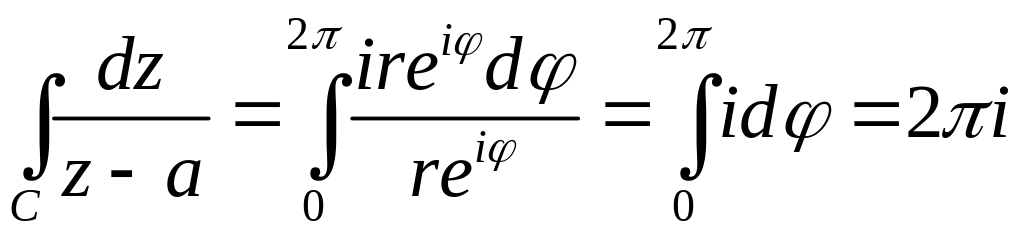 .
.
Выберем
r
настолько
малым, чтобы С
лежала внутри контура L.
В качестве области G
возьмём
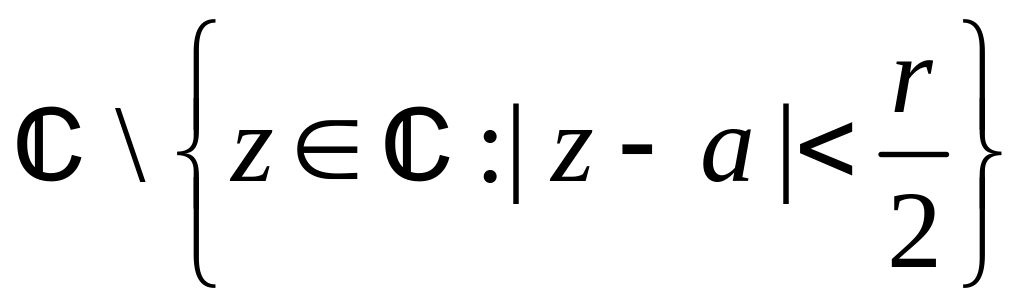 .
Тогда
.
Тогда![]() - аналитическая в G.
Кривые C
и L
образуют кольцеобразную область. Значит
(по следствию),
- аналитическая в G.
Кривые C
и L
образуют кольцеобразную область. Значит
(по следствию),
![]() .
Следовательно,
по
любому кусочно - гладкому контуру L,
охватывающему точку а.
.
Следовательно,
по
любому кусочно - гладкому контуру L,
охватывающему точку а.
