
- •§1. Комплексные числа и действия над ними
- •1.Понятие комплексного числа. Действия над комплексными числами
- •2. Геометрическая интерпретация комплексного числа.
- •3. Комплексная плоскость как метрическое пространство
- •§2.Последовательности комплексных чисел. Предел последовательности
- •§3. Расширенная комплексная плоскость
- •§4. Функции комплексного переменного
- •1. Комплексно-значные функции действительной переменной
- •2. Кривые на комплексной плоскости
- •3.Функции комплексного переменного
- •§5. Предел и непрерывность функции комплексного переменного
- •1. Предел функции комплексного переменного
- •2.Непрерывность функции комплексного переменного
- •§6. Геометрическая интерпретация функции комплексного переменного
- •§7.Дифференцирование функции одной комплексной переменной
- •1.Производная функции комплексной переменной
- •2. Необходимые и достаточные условия
- •3. Понятие аналитической функции
- •4. Гармонические функции
- •5. Восстановление аналитической функции
- •6. Геометрический смысл аргумента и модуля производной
- •7. Понятие о конформном отображении
- •§8. Простейшие элементарные функции комплексной переменной
- •1. Линейная функция
- •2. Дробно-линейная функция
- •3.Многочлен
- •4. Показательная функция
- •5. Тригонометрические функции
- •6. Гиперболические функции
- •7. Области однолистности аналитических функций. Обратные функции
- •8. Степенная функция и радикал
- •9. Логарифмическая функция
- •10. Общие степенная и показательная функции
- •§9. Интегрирование функций комплексного переменного
- •1.Понятие интеграла
- •2.Вычисление интеграла от функции комплексного переменного
- •3.Основные свойства интеграла от функции комплексного переменного
- •§10. Интегральная теорема Коши
- •§11. Первообразная
- •§12. Интегральная формула Коши и ее следствия
- •1. Интегральная формула Коши
- •2. Бесконечная дифференцируемость аналитической функции
- •3. Теорема Морера
- •4. Теорема о среднем
- •5. Принцип максимума модуля аналитической функции
§9. Интегрирование функций комплексного переменного
1.Понятие интеграла
Пусть
на комплексной плоскости
задана кривая L,
которая является простой и гладкой,
т.е.
![]() ,
причем
,
причем
а)
функции x(t)
и y(t)
непрерывно дифференцируемы на [,]
и
![]()
![]() (гладкая кривая),
(гладкая кривая),
б) различным значениям параметра t соответствуют различные точки кривой L (простая кривая).
Точки z() и z()- начало и конец кривой L. Если z()=z(), то кривая называется замкнутой.
П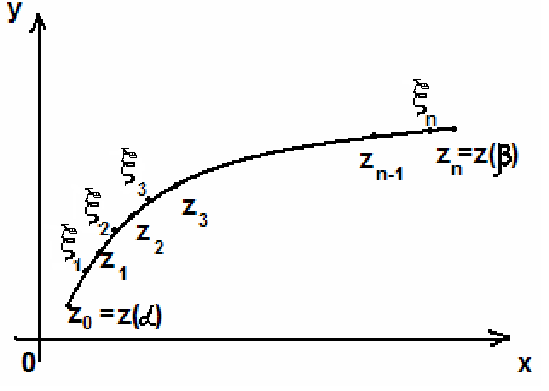 усть
на кривой
усть
на кривой
![]() (т.е.
в каждой ее точке) определена функция
комплексного переменного f(z).
(т.е.
в каждой ее точке) определена функция
комплексного переменного f(z).
Пусть
T-
произвольное разбиение кривой L
точками
![]() ,
взятыми в порядке возрастания параметра
t,
на частичные дуги
,
взятыми в порядке возрастания параметра
t,
на частичные дуги
![]() .
Обозначим через
.
Обозначим через
![]() длину дуги
.
На каждой частичной дуге
выберем произвольную точку
длину дуги
.
На каждой частичной дуге
выберем произвольную точку
![]() .
Обозначим
.
Обозначим
![]() ,
,
![]() ,
,
![]() .
.
Составим интегральную сумму для функции f(z) по кривой L,соответствующую данному разбиению T и выбору точек :
 . (1)
. (1)
Определение.
Если
существует конечный предел интегральной
суммы (1) при
![]() (или
при
(или
при
![]() ),
не зависящий ни от способа разбиения
T
кривой L,
ни от выбора точек
,
то этот предел называется интегралом
от функции f(z)
по кривой L
и обозначается
),
не зависящий ни от способа разбиения
T
кривой L,
ни от выбора точек
,
то этот предел называется интегралом
от функции f(z)
по кривой L
и обозначается
![]() .
.
Таким
образом,
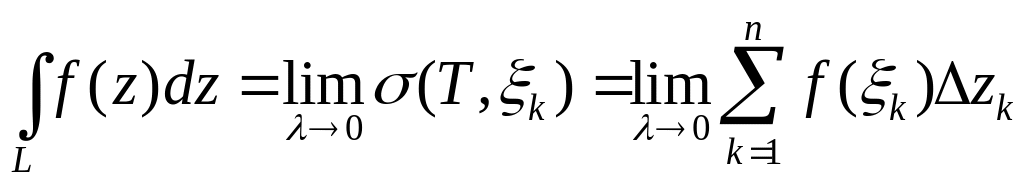 .
.
В этом случае функция f(z) называется интегрируемой по кривой L.
Теорема
1 (достаточное
условие существования интеграла от
функции комплексного переменного).
Пусть L
– простая гладкая кривая на
,
f(z)=u(x;y)+iv(x;y)
непрерывна на L.
Тогда существует
![]() ,
причем справедливо равенство:
,
причем справедливо равенство:
![]() . (2)
. (2)
Доказательство.
Выберем
произвольно разбиение T
кривой L
на дуги
,
на каждой
выберем произвольно точку
.
Составим интегральную сумму
.
Выделим в
![]() действительную и мнимые части:
действительную и мнимые части:
z=x+iy,
f(z)=u(x;y)+iv(x;y),
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() .
Тогда
.
Тогда
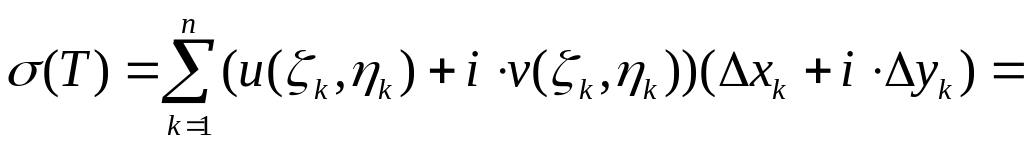
 . (3)
. (3)
В правой
части (3) стоят интегральные суммы для
криволинейных интегралов II
типа двух действительных функций u(x;y)
и v(x;y).
Если
![]() и
и
![]() ,
то и
,
то и
![]()
![]() (или
).
(или
).
Т.к. L – гладкая кривая, а функции u(x;y) и v(x;y) непрерывны на L, то

![]()
и  .
.
Тогда существует предел при левой части (3), т.е. существует .
Переходя в (3) к пределу при , получим (2).
2.Вычисление интеграла от функции комплексного переменного
Пусть вначале f(t)=u(t)+iv(t) –комплексно-значная функция действительной переменной. Тогда интеграл от f(t) по отрезку [a;b] определяется следующим образом:
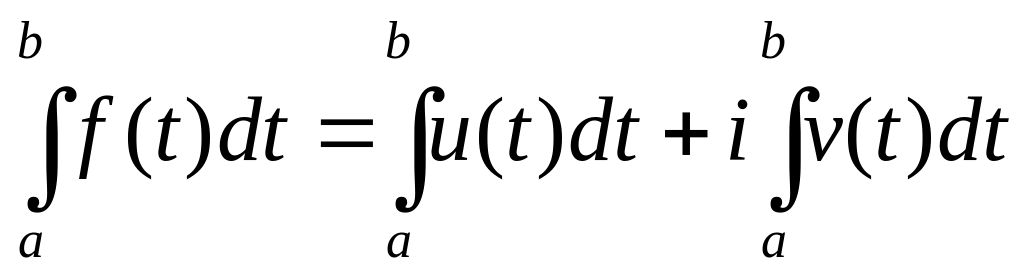 .
.
Рассмотрим теперь интеграл от функции комплексного переменного по кривой L.
Теорема 2.Пусть L – простая гладкая кривая, заданная параметрически:
L:
z(t)=x(t)+iy(t),
t,
функция f(z)
непрерывна на L.
Тогда справедливо равенство:
 (где
(где
![]() ).
).
Доказательство.
Т.к. выполнены условия теоремы 1, то имеет место равенство (2) . Каждый криволинейный интеграл II типа можно заменить по формуле, сводящей его вычисление к вычислению обычного определенного интеграла:
![]()


= .
.
Пример
1. Вычислить
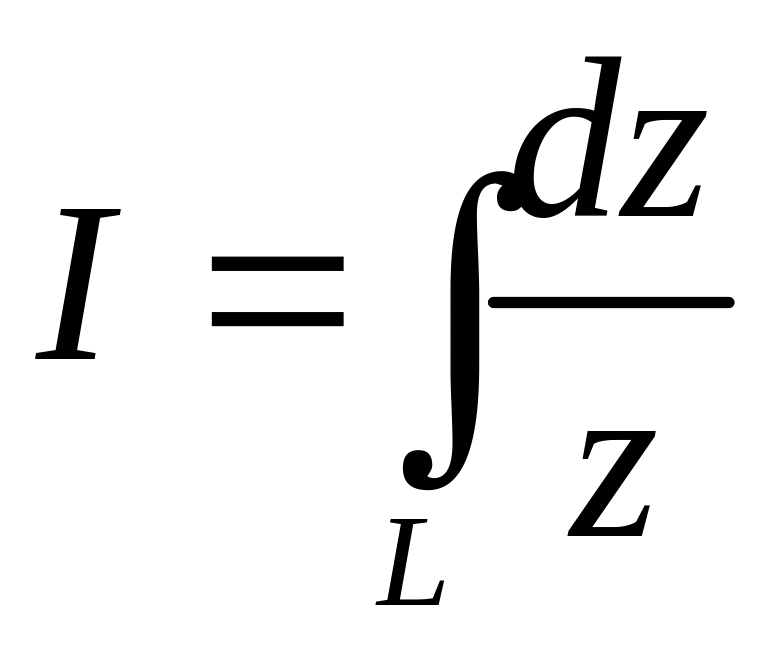 ,
L:
,
L:
![]() -
окружность радиуса r
с центром в точке (0;0).
-
окружность радиуса r
с центром в точке (0;0).
L: (
 )
– простой гладкий замкнутый контур.
Тогда
)
– простой гладкий замкнутый контур.
Тогда
 .
.
Пример
2. Вычислить
![]() ,
где L
– произвольная гладкая кривая
z(t)=x(t)+iy(t),
,
где L
– произвольная гладкая кривая
z(t)=x(t)+iy(t),
![]() ,
,
![]() .
.
 =
=![]() .
.
Таким образом, интеграл не зависит от кривой L, а зависит только от начальной и конечной точек.
Если
z()=z(),
т.е. L
– замкнутая кривая, то
![]() .
.
Если
![]() ,
то
,
то
![]() .
.
