
- •§1. Комплексные числа и действия над ними
- •1.Понятие комплексного числа. Действия над комплексными числами
- •2. Геометрическая интерпретация комплексного числа.
- •3. Комплексная плоскость как метрическое пространство
- •§2.Последовательности комплексных чисел. Предел последовательности
- •§3. Расширенная комплексная плоскость
- •§4. Функции комплексного переменного
- •1. Комплексно-значные функции действительной переменной
- •2. Кривые на комплексной плоскости
- •3.Функции комплексного переменного
- •§5. Предел и непрерывность функции комплексного переменного
- •1. Предел функции комплексного переменного
- •2.Непрерывность функции комплексного переменного
- •§6. Геометрическая интерпретация функции комплексного переменного
- •§7.Дифференцирование функции одной комплексной переменной
- •1.Производная функции комплексной переменной
- •2. Необходимые и достаточные условия
- •3. Понятие аналитической функции
- •4. Гармонические функции
- •5. Восстановление аналитической функции
- •6. Геометрический смысл аргумента и модуля производной
- •7. Понятие о конформном отображении
- •§8. Простейшие элементарные функции комплексной переменной
- •1. Линейная функция
- •2. Дробно-линейная функция
- •3.Многочлен
- •4. Показательная функция
- •5. Тригонометрические функции
- •6. Гиперболические функции
- •7. Области однолистности аналитических функций. Обратные функции
- •8. Степенная функция и радикал
- •9. Логарифмическая функция
- •10. Общие степенная и показательная функции
- •§9. Интегрирование функций комплексного переменного
- •1.Понятие интеграла
- •2.Вычисление интеграла от функции комплексного переменного
- •3.Основные свойства интеграла от функции комплексного переменного
- •§10. Интегральная теорема Коши
- •§11. Первообразная
- •§12. Интегральная формула Коши и ее следствия
- •1. Интегральная формула Коши
- •2. Бесконечная дифференцируемость аналитической функции
- •3. Теорема Морера
- •4. Теорема о среднем
- •5. Принцип максимума модуля аналитической функции
2. Геометрическая интерпретация комплексного числа.
Модуль и аргумент комплексного числа
В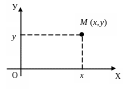 ыберем
на плоскости систему координат. Между
точками пространства
и точками координатной плоскости можно
установить взаимно-однозначное
соответствие: z=x+i·y=(x;y)
↔M(x;y).
ыберем
на плоскости систему координат. Между
точками пространства
и точками координатной плоскости можно
установить взаимно-однозначное
соответствие: z=x+i·y=(x;y)
↔M(x;y).
Т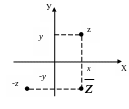 огда
точку М(х;у)
можно рассматривать как изображение
комплексного числа z=x+i·y.
При таком отображении действительные
числа изображаются точками оси абсцисс.
Ось ОХ
называется действительной осью. Чисто
мнимые комплексные числа изображаются
точками оси ординат. Ось ОУ
– мнимая ось. Плоскость, точки которой
изображают комплексные числа, называется
комплексной
плоскостью.
огда
точку М(х;у)
можно рассматривать как изображение
комплексного числа z=x+i·y.
При таком отображении действительные
числа изображаются точками оси абсцисс.
Ось ОХ
называется действительной осью. Чисто
мнимые комплексные числа изображаются
точками оси ординат. Ось ОУ
– мнимая ось. Плоскость, точки которой
изображают комплексные числа, называется
комплексной
плоскостью.
Комплексные
числа z
и –z
изображаются точками, симметричными
относительно начала координат.
Комплексные числа z
и
![]() –
точками, симметричными относительно
ОХ.
–
точками, симметричными относительно
ОХ.
Можно установить взаимно-однозначное соответствие между точками пространства и множеством радиус-векторов точек координатной плоскости. То есть комплексное число z изображается вектором с началом в точке О и концом в точке z. При таком изображении комплексного числа z=x+i·y, числа x и у – проекции радиус-вектора z на оси координат.
Расстояние
от точки О(0,0)
до точки z
равно
![]() =
=![]() .
.
Определение.
Модулем
комплексного числа z=x+i·y
называется
действительное неотрицательное число
|z|=![]() .
.
Отсюда видно, что
|z|≥|x|=|Rez|, |z|≥|y|=|Imz|, |z|≤|Rez|+|Imz|.
И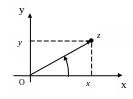 сходя
из векторной интерпретации комплексных
чисел, можно дать геометрическое
истолкование сложения и вычитания
комплексных чисел как сложение и
вычитание соответствующих радиус-векторов.
Расстояние между точками z1
и
z2
равно |z1-z2|.
сходя
из векторной интерпретации комплексных
чисел, можно дать геометрическое
истолкование сложения и вычитания
комплексных чисел как сложение и
вычитание соответствующих радиус-векторов.
Расстояние между точками z1
и
z2
равно |z1-z2|.
Пусть r – длина радиус-вектора z (r=|z|), a φ - угол между положительным направлением оси ОХ и вектором z, то есть (r;φ) – полярные координаты точки M(x;y), z=x+i·y. Число φ называется аргументом комплексного числа z и обозначается: Arg z (-∞<φ< ∞).
Для числа z=0 аргумент не определён.
Для любого комплексного числа (кроме z=0) Arg z может быть найден из системы
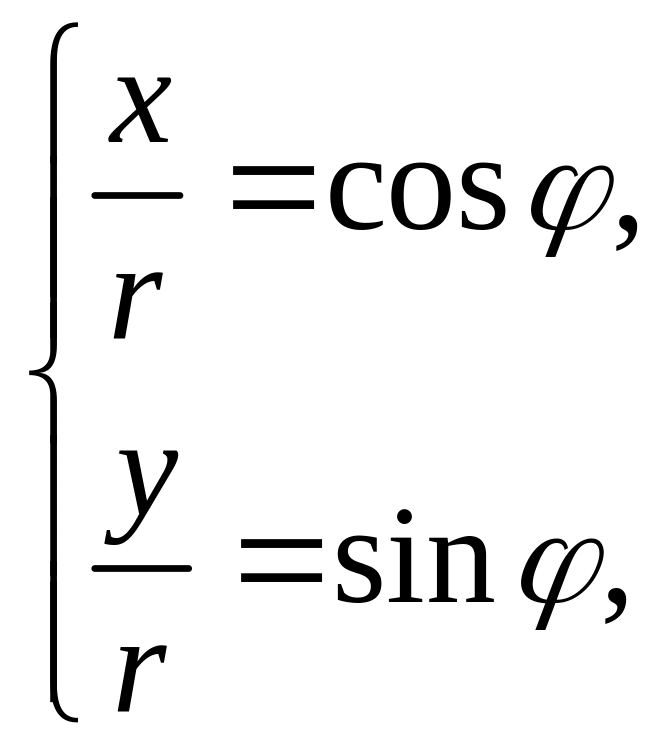
которая имеет, вообще говоря, бесконечное множество решений. Все они содержатся в формуле φ=φ0+2πk, k , где φ0–одно из решений системы.
Значение φ0, удовлетворяющее условию -π <φ0<π , называется главным значением аргумента и обозначается: arg z. Таким образом,
Arg z=argz+2πk, k .
Так как x=rcosφ, y=rsinφ, то
z=x+i·y=rcosφ+i·rsinφ,
z=r(cosφ+i·sinφ) -
тригонометрическая форма записи комплексного числа.
Действия с комплексными числами, записанными в тригонометрической форме
Пусть α=r(cosφ+i·sinφ), β=ρ(cosψ+i·sinψ).
1) α·β=rρ(cosφ+i·sinφ)·(cosψ+i·sinψ)=
=rρ(cosφcosψ-sinφsinψ+i(sinφcosψ+cosφsinψ))=rρ(cos(φ+ψ)+sin(φ+ψ)).
То есть
|α·β|=r·ρ=|α|·|β|, Arg(α·β)=φ+ψ=Argα+Argβ.
Модуль произведения двух комплексных чисел равен произведению их модулей, аргумент произведения двух комплексных чисел равен сумме аргументов сомножителей.
Это правило распространяется на случай любого конечного числа сомножителей.
2) В частности, если все сомножители равны, получим
|αⁿ|=|α|ⁿ, Arg(αⁿ)=nArg(α), или
αⁿ=(r(cosφ+isinφ))ⁿ=rⁿ(cos(nφ)+isin(nφ)) – формула Муавра.
3) Пусть α ≠0. Корнем натуральной степени из комплексного числа α называется такое комплексное число β, которое будучи возведено в n-ю степень даёт число α, то есть βn=α.
Очевидно, |![]() |=
|=![]() ,
, ![]()
![]() .
.
Или если α= r(cosφ+i·sinφ), то
![]() =
=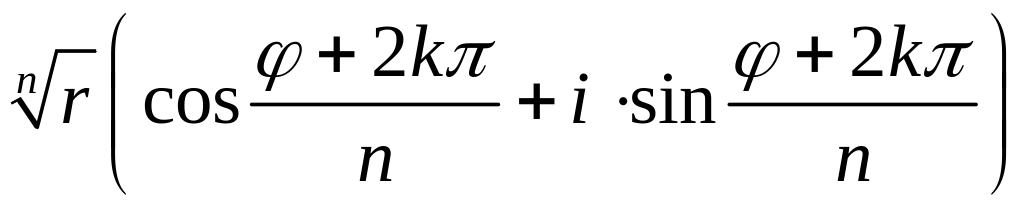 ,
k
=
0, 1, 2, …, n-1,
-π<φ≤π.
,
k
=
0, 1, 2, …, n-1,
-π<φ≤π.
То есть
среди значений
различными являются только n.
Геометрически они изображаются вершинами
правильного n-угольника,
вписанного в окружность с центром в
точке О(0;0),
радиуса
![]() .
.
4) Так
как по определению частного
![]() ,
то из 1) следует |β|=
,
то из 1) следует |β|=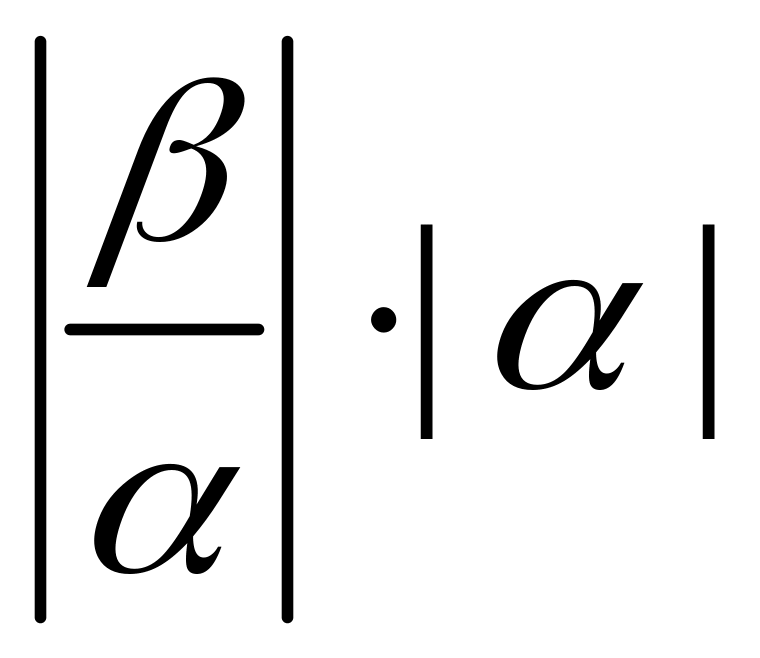 ,
Argβ=Arg
,
Argβ=Arg![]() +Argα.
Отсюда
+Argα.
Отсюда
![]() =
=![]() , Arg
=Argβ-Argα.
, Arg
=Argβ-Argα.
Модуль частного двух комплексных чисел равен частному их модулей, аргумент частного двух комплексных чисел равен разности аргументов делимого и делителя.
5) Используя геометрическую интерпретацию комплексных чисел с помощью радиус-векторов, легко получить соотношения для модуля суммы и разности двух комплексных чисел.
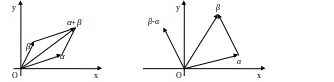 |α+β|≤|α|+|β| Так
как |α|+|β-α|≥|β|
и
|β|+|β-α|≥|α|,
то из
|α+β|≤|α|+|β| Так
как |α|+|β-α|≥|β|
и
|β|+|β-α|≥|α|,
то из
|β-α|≥|β|-|α| и |β-α|≥|α|-|β| следует
|β-α|≥||β|-|α||.
Имеет место соотношение
eiφ=cosφ+i·sinφ – формула Эйлера (более общий вид – позже).
Отсюда получается показательная форма записи комплексного числа
z=reiφ.
В показательной форме операции над комплексными числами принимают более наглядный вид.
Пусть α= reiφ, β=ρeiψ. Тогда
α β=rρei(φ+ψ),
αⁿ=rⁿ einφ,
=![]()
![]() ,-π<φ≤π,
k=1,
2, …, n-1,
,-π<φ≤π,
k=1,
2, …, n-1,
![]() =
=![]()
![]() ,
α0.
,
α0.
