
- •§1. Комплексные числа и действия над ними
- •1.Понятие комплексного числа. Действия над комплексными числами
- •2. Геометрическая интерпретация комплексного числа.
- •3. Комплексная плоскость как метрическое пространство
- •§2.Последовательности комплексных чисел. Предел последовательности
- •§3. Расширенная комплексная плоскость
- •§4. Функции комплексного переменного
- •1. Комплексно-значные функции действительной переменной
- •2. Кривые на комплексной плоскости
- •3.Функции комплексного переменного
- •§5. Предел и непрерывность функции комплексного переменного
- •1. Предел функции комплексного переменного
- •2.Непрерывность функции комплексного переменного
- •§6. Геометрическая интерпретация функции комплексного переменного
- •§7.Дифференцирование функции одной комплексной переменной
- •1.Производная функции комплексной переменной
- •2. Необходимые и достаточные условия
- •3. Понятие аналитической функции
- •4. Гармонические функции
- •5. Восстановление аналитической функции
- •6. Геометрический смысл аргумента и модуля производной
- •7. Понятие о конформном отображении
- •§8. Простейшие элементарные функции комплексной переменной
- •1. Линейная функция
- •2. Дробно-линейная функция
- •3.Многочлен
- •4. Показательная функция
- •5. Тригонометрические функции
- •6. Гиперболические функции
- •7. Области однолистности аналитических функций. Обратные функции
- •8. Степенная функция и радикал
- •9. Логарифмическая функция
- •10. Общие степенная и показательная функции
- •§9. Интегрирование функций комплексного переменного
- •1.Понятие интеграла
- •2.Вычисление интеграла от функции комплексного переменного
- •3.Основные свойства интеграла от функции комплексного переменного
- •§10. Интегральная теорема Коши
- •§11. Первообразная
- •§12. Интегральная формула Коши и ее следствия
- •1. Интегральная формула Коши
- •2. Бесконечная дифференцируемость аналитической функции
- •3. Теорема Морера
- •4. Теорема о среднем
- •5. Принцип максимума модуля аналитической функции
10. Общие степенная и показательная функции
Введем понятие степени с произвольным показателем.
Пусть
а0
–произвольное число. Если
![]() ,
то, как известно
,
то, как известно
an=|a|n(cos(nArga)+isin(nArga)),
если ,
где
![]() и
и
![]() - несократимая дробь, то
- несократимая дробь, то
![]() ,
,
где
![]() -
единственное действительное положительное
значение степени числа |a|.
-
единственное действительное положительное
значение степени числа |a|.
Пусть - иррациональное число. Зафиксируем =Arga и рассмотрим последовательность {rn} рациональных чисел, сходящуюся к тогда
![]() .
.
Это значение примем за одно из значений степени a. Чтобы получить остальные значения, будем придавать Arga различные значения. Так как два различных значения Arga отличаются на 2k, а это число не может быть целым кратным 2 (так как - иррациональное число), то все значения a, соответствующие различным значениям Arga различны.
Итак, если , то
), (21)
Причем,
если
![]() ,
то получаем одно значение, если
,
то получаем одно значение, если
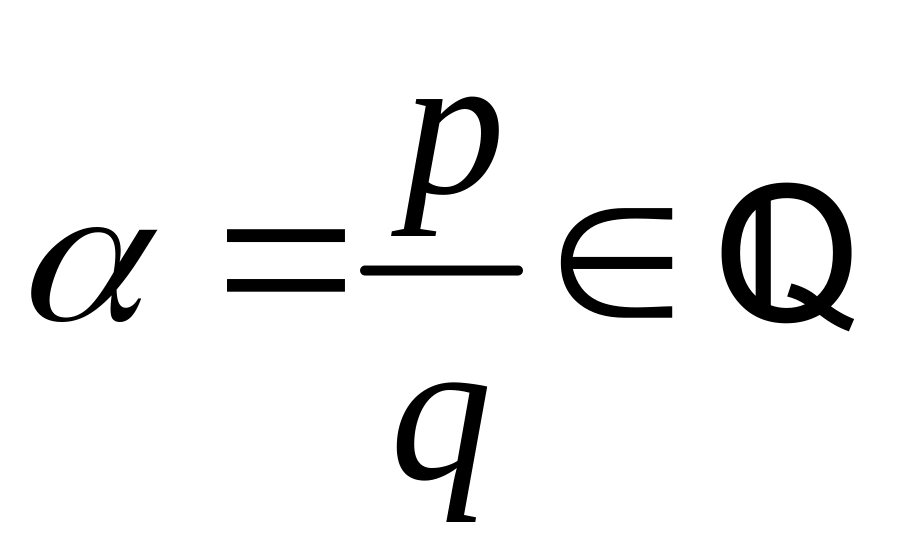 ,то q
значений, и если
- иррациональное число, то бесконечное
множество значений.
,то q
значений, и если
- иррациональное число, то бесконечное
множество значений.
Пусть . Формулу (21) можно записать в виде:
a=eln|a|(cos(Arga)+isin(Arga))=exp(ln|a|+iArga)=
=exp((ln|a|+iArga))=exp(Lna).
Определение. Пусть . Степенью комплексного числа а называется
a= exp(Lna).
Замечание. Для степени с произвольным показателем, вообще говоря,
1)
![]() , 2)
, 2)
![]() .
.
![]() ,
,
![]()
![]() .
.
С
другой стороны,
![]() .
Значит, в общем случае
.
.
Значит, в общем случае
.
Пример. Покажем, что
![]() ,k=0,1.
,k=0,1.
 ,
,  ,
,
тогда
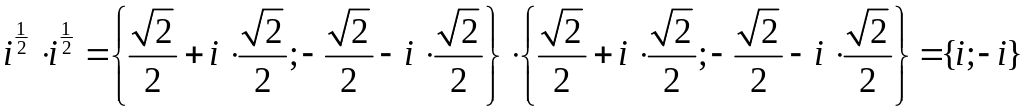
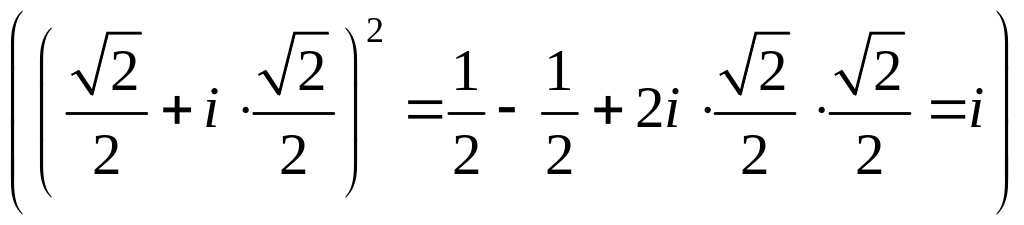 .
.
С
другой стороны,
![]() .
Множества
в правых и левых частях не равны.
.
Множества
в правых и левых частях не равны.
Определение. Степенной функцией комплексной переменного называется функция вида
f(z)=![]() =exp(Lnz),
=exp(Lnz),![]() . (22)
. (22)
Она
определена вообще
![]() .
Степенная функция в общем случае (но
не всегда!) многозначна. Если
.
Степенная функция в общем случае (но
не всегда!) многозначна. Если
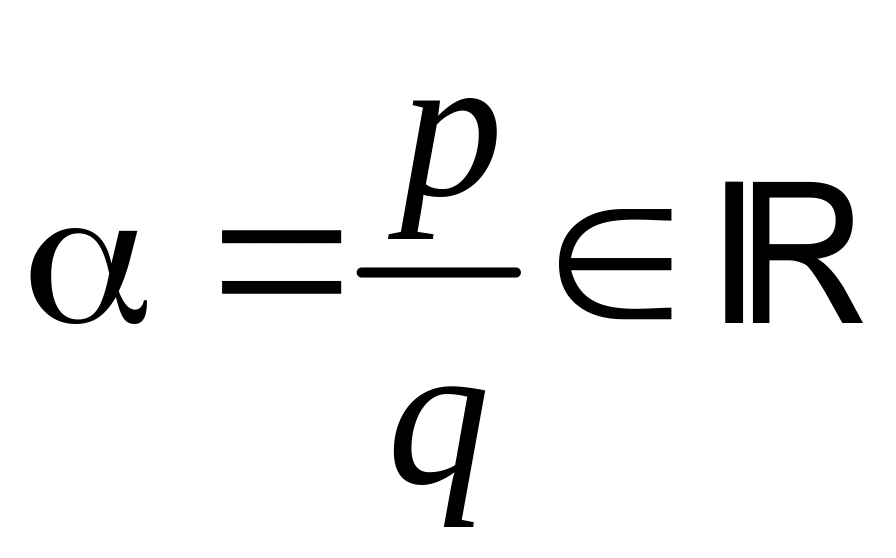 ,
то –конечнозначна (
,
то –конечнозначна (![]() -значна),
если
-значна),
если![]() ,
то- бесконечнозначна.
,
то- бесконечнозначна.
Каждому
значению независимой переменной z
соответствует счетное множество
значений степени z.
Если справа в (22) брать одну определенную
ветвь Lnz,то
будем получать
соответствующие
ветви степенной функции. Например,
![]() .
.
Отдельные
ветви, т.е. однозначные функции
![]() являются аналитическими функциями на
комплексной плоскости с разрезом вдоль
отрицательной действительной полуоси.
По правилу производной сложной функции:
являются аналитическими функциями на
комплексной плоскости с разрезом вдоль
отрицательной действительной полуоси.
По правилу производной сложной функции:
![]() .
.
Например,![]() .
.
Определение. Функция вида
![]() , (24)
, (24)
где , , называется общей показательной функцией.
Эта
функция многозначна в силу многозначности
Lna.
Чтобы получить определенную однозначную
ветвь, надо фиксировать одно из значений
![]() .
.
Пусть![]() ,тогда
,тогда![]() ,
,
![]() .
.
При
![]() ,
т.е. когда берем главное значение Lne,
получим
,
т.е. когда берем главное значение Lne,
получим
![]() ,
т.е. это значение совпадает с изученной
нами функцией
,
т.е. это значение совпадает с изученной
нами функцией
![]() .
.
Зафиксируем
![]() функции
функции
![]() одно из значений логарифма:
одно из значений логарифма:
![]() .
Тогда мы получим однозначную ветвь
функции
.
Тогда мы получим однозначную ветвь
функции
![]() и можем рассмотреть обратную к ней
функцию. Получим
и можем рассмотреть обратную к ней
функцию. Получим
![]() .
.
Так
как
![]() ,
то w
можно рассматривать как логарифм z
по основанию a.
,
то w
можно рассматривать как логарифм z
по основанию a.
Определение.
Логарифмом
произвольного комплексного числа
![]() по некоторому основанию a
(
-комплексное
число) называется
по некоторому основанию a
(
-комплексное
число) называется
![]() ,
,
где в знаменателе стоит одно фиксированное значение Lna.
