
- •§1. Комплексные числа и действия над ними
- •1.Понятие комплексного числа. Действия над комплексными числами
- •2. Геометрическая интерпретация комплексного числа.
- •3. Комплексная плоскость как метрическое пространство
- •§2.Последовательности комплексных чисел. Предел последовательности
- •§3. Расширенная комплексная плоскость
- •§4. Функции комплексного переменного
- •1. Комплексно-значные функции действительной переменной
- •2. Кривые на комплексной плоскости
- •3.Функции комплексного переменного
- •§5. Предел и непрерывность функции комплексного переменного
- •1. Предел функции комплексного переменного
- •2.Непрерывность функции комплексного переменного
- •§6. Геометрическая интерпретация функции комплексного переменного
- •§7.Дифференцирование функции одной комплексной переменной
- •1.Производная функции комплексной переменной
- •2. Необходимые и достаточные условия
- •3. Понятие аналитической функции
- •4. Гармонические функции
- •5. Восстановление аналитической функции
- •6. Геометрический смысл аргумента и модуля производной
- •7. Понятие о конформном отображении
- •§8. Простейшие элементарные функции комплексной переменной
- •1. Линейная функция
- •2. Дробно-линейная функция
- •3.Многочлен
- •4. Показательная функция
- •5. Тригонометрические функции
- •6. Гиперболические функции
- •7. Области однолистности аналитических функций. Обратные функции
- •8. Степенная функция и радикал
- •9. Логарифмическая функция
- •10. Общие степенная и показательная функции
- •§9. Интегрирование функций комплексного переменного
- •1.Понятие интеграла
- •2.Вычисление интеграла от функции комплексного переменного
- •3.Основные свойства интеграла от функции комплексного переменного
- •§10. Интегральная теорема Коши
- •§11. Первообразная
- •§12. Интегральная формула Коши и ее следствия
- •1. Интегральная формула Коши
- •2. Бесконечная дифференцируемость аналитической функции
- •3. Теорема Морера
- •4. Теорема о среднем
- •5. Принцип максимума модуля аналитической функции
8. Степенная функция и радикал
Определение.
Степенной
называется функция вида
![]() .
.
Если
![]() ,
то
,
то
![]() .
Следовательно,
.
Следовательно,
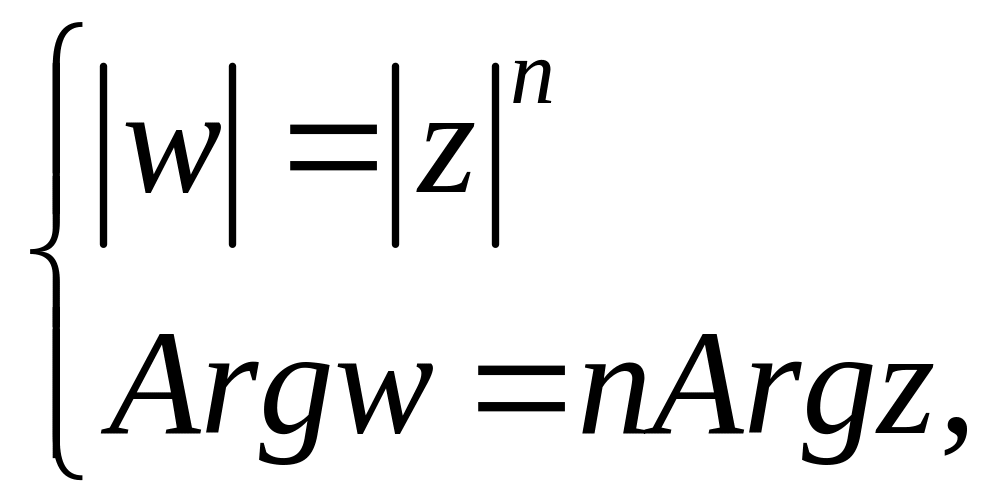
![]()
![]()
![]() -
многолистная функция.
-
многолистная функция.
![]() ,
при
,
при
![]() .
Следовательно,
.
Следовательно,
![]() -аналитическая
в
функция.
-аналитическая
в
функция.
Функция
обладает основными свойствами функции
![]() действительного переменного:
действительного переменного:
![]()
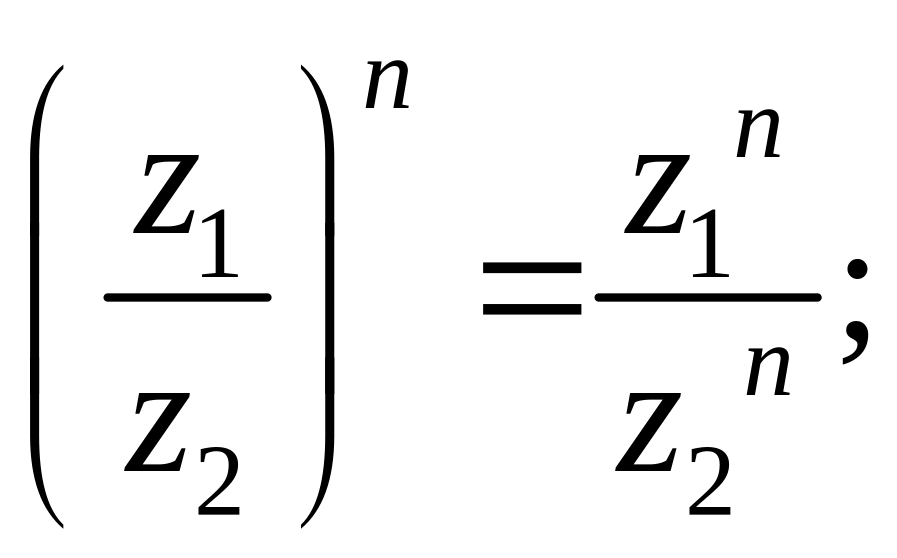
![]() .
.
Найдем
области однолистности функции
.
Выберем
произвольные
![]() ,
,
![]()
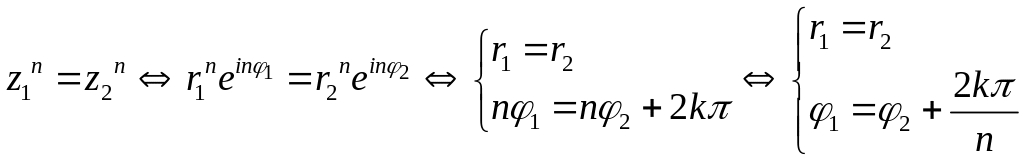
![]()
С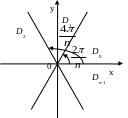 ледовательно,
областью однолистности функции
будет любой угол с вершиной в начале
координат и раствором
ледовательно,
областью однолистности функции
будет любой угол с вершиной в начале
координат и раствором![]() :
:
![]()
Если
![]() ,
то
,
то
![]() .
.
Рассмотрим
радикал
![]() -
функцию обратную к функции
-
функцию обратную к функции
![]() .
Пусть
.
Пусть
![]() т.е.
т.е.
![]() ,
тогда
,
тогда
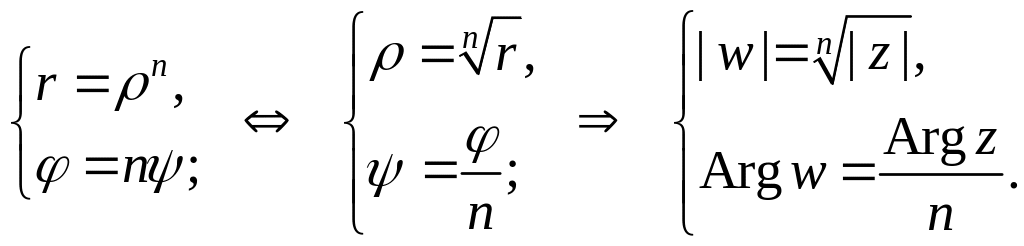 .
.
Следовательно,
![]() радикал имеет n
различных значений, которые выражаются
формулой
радикал имеет n
различных значений, которые выражаются
формулой
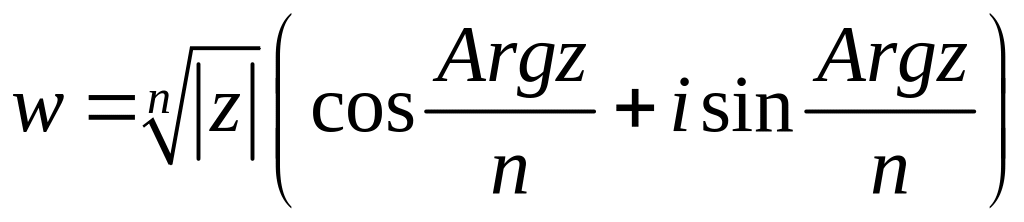
Следовательно,
функция
является
многозначной (n
– значной). Эти n
значений располагаются в вершинах
правильного n
– угольника, вписанного в окружность
![]() .
При
.
При
![]() и
и
![]() получаем по одному значению функции
получаем по одному значению функции
![]() и
и
![]() .
.
Чтобы
выделить однозначную ветвь, достаточно
указать, в какой области однолистности
изменяется w.
Мы установили выше, что областью
однолистности функции
![]() является
угол с вершиной в начале координат и
раствором
:
является
угол с вершиной в начале координат и
раствором
:
![]()
Любой
луч плоскости (
)
![]() при
отображении
переходит
в луч плоскости (z):
при
отображении
переходит
в луч плоскости (z):
![]() .
Если луч
пробегает
область
.
Если луч
пробегает
область
![]() против хода часовой стрелки, то луч
пробежит всю плоскость (z)
от
против хода часовой стрелки, то луч
пробежит всю плоскость (z)
от
![]() до
до
![]() .
Следовательно, любая из областей
однолистности
перейдет в одну и ту же область
.
Следовательно, любая из областей
однолистности
перейдет в одну и ту же область
![]() плоскости (z):
угол раствора 2π,
границей которой служит луч
плоскости (z):
угол раствора 2π,
границей которой служит луч
![]() .
.
Т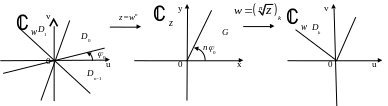 аким
образом, в области
получаем n
однозначных ветвей функции
Каждая из них определяется условием,
что ее значения
принадлежат области
.
Будем обозначать эти ветви
аким
образом, в области
получаем n
однозначных ветвей функции
Каждая из них определяется условием,
что ее значения
принадлежат области
.
Будем обозначать эти ветви
![]() .
.
Т.к.
![]() имеет
отличную от нуля производную во всех
точках
имеет
отличную от нуля производную во всех
точках
![]() ,
то обратные функции
имеют отличные от нуля производные:
,
то обратные функции
имеют отличные от нуля производные:
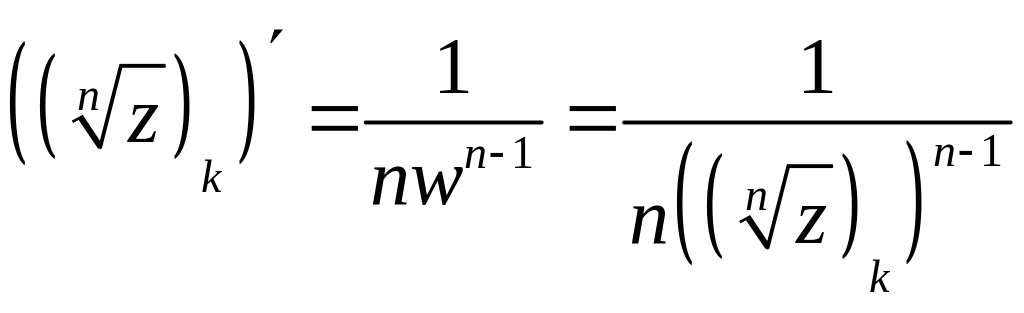 .
.
Зафиксируем
какое-либо значение
![]() .
Пусть точка z
описывает в плоскости (z)
некоторую кривую, содержащую внутри
начало координат. Тогда после полного
обхода Argz
изменится на 2π
(увеличится, если – против хода часовой
стрелки и уменьшится, если по ходу).
Следовательно, значение
.
Пусть точка z
описывает в плоскости (z)
некоторую кривую, содержащую внутри
начало координат. Тогда после полного
обхода Argz
изменится на 2π
(увеличится, если – против хода часовой
стрелки и уменьшится, если по ходу).
Следовательно, значение
![]() в первом случае перейдет от
к
в первом случае перейдет от
к
![]() (
(![]() перейдет в
перейдет в
![]() ),
а во втором - от
к
),
а во втором - от
к
![]() (
перейдет к
).
(
перейдет к
).
Определение. Точка, обладающая тем свойством, что обход вокруг нее переводит от одной ветви многозначной функции к другой, называется точкой разветвления этой функции.
Таким
образом, точка z=0
– точка разветвления для функции
.
Так как полный поворот от одной ветви
многозначной функции к другой на угол
2
является
в тоже время и полным оборотом вокруг
точки z=
(то есть обход по окружности бесконечно
большого радиуса с центром в начале
координат), то z=![]() - тоже точка разветвления.
- тоже точка разветвления.
Итак, многозначная функция имеет 2 точки разветвления: z=0 и z=.
Если после n-кратного обхода вокруг точки разветвления вновь возвратимся к исходной ветви, но говорят, что эта точка является точкой разветвления (n-1)-го порядка. Следовательно, z=0 и z= - точки разветвления (n-1)-го порядка функции .
