6. Гиперболические функции

Определение. Гиперболический косинус ,

гиперболический синус . (19)

Свойства chz и shz

1 Для chz=chx и shz=shx.

2 ch(-z)=chz и sh(-z)=-shz.

3 chz=cos(iz) и shz=-isin(iz) (20)

(или sin(iz)=ishz)

,

.

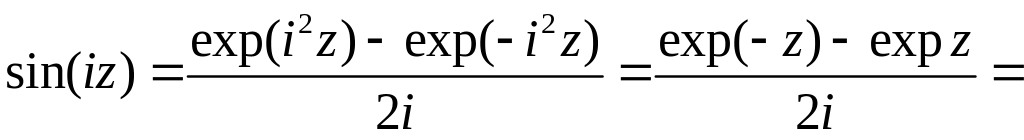
4 Из (20) следует .

5 chz и shz аналитические в

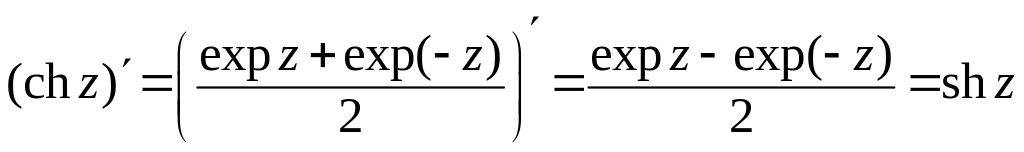
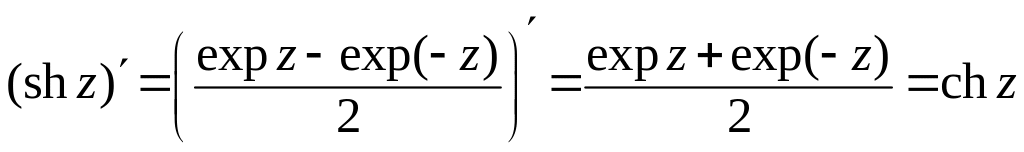
6 chz и shz - периодические с периодом .

Вернемся к sinz и cosz.

Определим их действительные, мнимые части и модули.

Покажем, что и - неограниченные функции.

,

.

Отсюда следует

,

.

(эти соотношения можно получить из (15)).

Т.к. 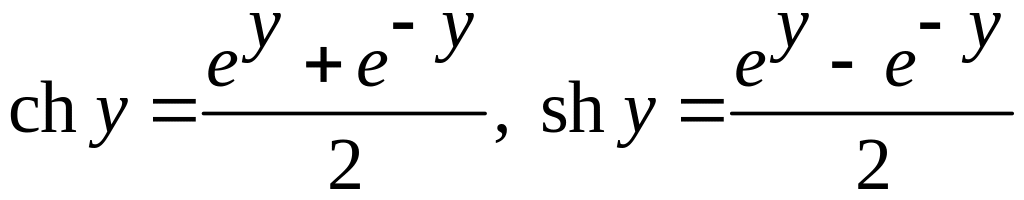, то из последних соотношений заключаем:

при , т. е. sinz и cosz- неограниченные функции.

7. Области однолистности аналитических функций. Обратные функции

Пусть функция w=f(z) - аналитическая в области D. Пусть G - образ области D при отображении w=f(z), т.е. G=f(D).

Определение. Если (т.е. в различных точках области D функция принимает различные значения), то аналитическая функция w=f(z) называется однолистной в области D.

Другими словами, однолистная функция w=f(z) взаимно однозначно отображает область D на G.

При однолистном отображении w=f(z) прообраз любой точки wG состоит из единственного элемента: : .

Поэтому z можно рассматривать как функцию от переменной , определенную на G. Она обозначается и называется обратной функцией.

Справедливы тождества:

и имеет место

Теорема. Если f(z)- однолистная и аналитическая на D, и на D, то - аналитическая на G=f(D).

Определение. Если в области D существует, по крайней мере, одна пара точек , то функцию f(z) называют многолистной в области D.

Если отображение w=f(z) является многолистным на D (например, w=e^z, w=sinz, w=cosz, w=zⁿ), то в этом случае некоторым значениям wG соответствует более, чем одна точка zD: f(z)=w.

Следовательно, обратное отображение не является однозначным, оно является многозначной функцией.

Определение. Функция w=f(z) называется многозначной функцией на множестве E, если некоторыми значениям zE соответствует более чем одно значение w.

Теорема. Если аналитическая функция w=f(z) многолистна в области D, то эту область можно разбить на конечное или счетное множество областей, в каждой из которых функция f(z) является однолистной.

К многозначным функциям неприменимы понятия аналитичности и непрерывности. Они могут применяться только к однозначным функциям. Для того, чтобы их использовать, выделяют однозначные ветви многозначных функций.

Определение. Однозначная на области D функция w=f(z) называется ветвью многозначной функции F, если значение f в любой точке zD совпадает с одним из значений F в этой точке.

Е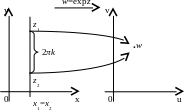 сли функция w=f(z) многолистна на D, то обратная функция будет многозначной. Чтобы выделить однозначную ветвь этой функции поступают, следующим образом: область D разбивают на области однолистности функции w=f(z) так, что никакие две из областей не имеют общих внутренних точек и так, чтобы каждая точка zD принадлежала одной из этих областей или границе некоторых из них. В каждой из этих областей однолистности определяют функцию, обратную к w=f(z). Она и является однозначной ветвью многозначной функции .

Н айдем области однолистности функции expz. Выберем

.

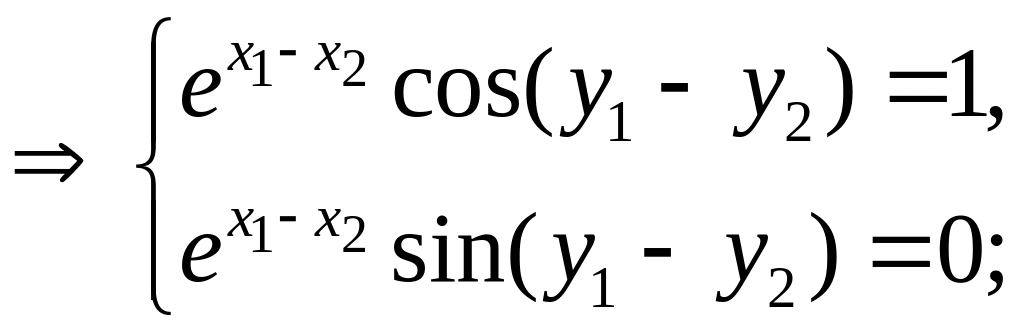
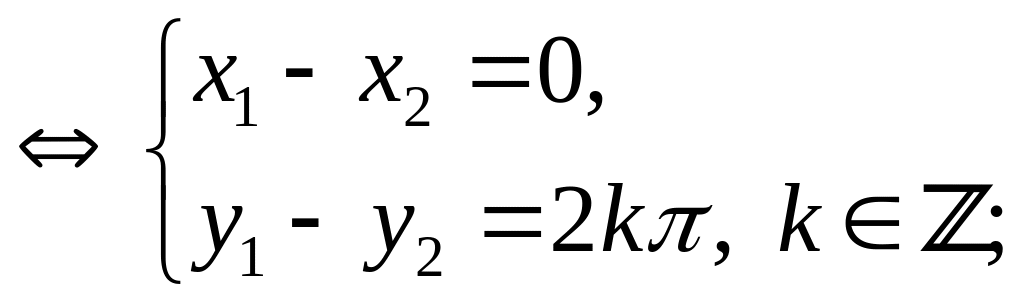
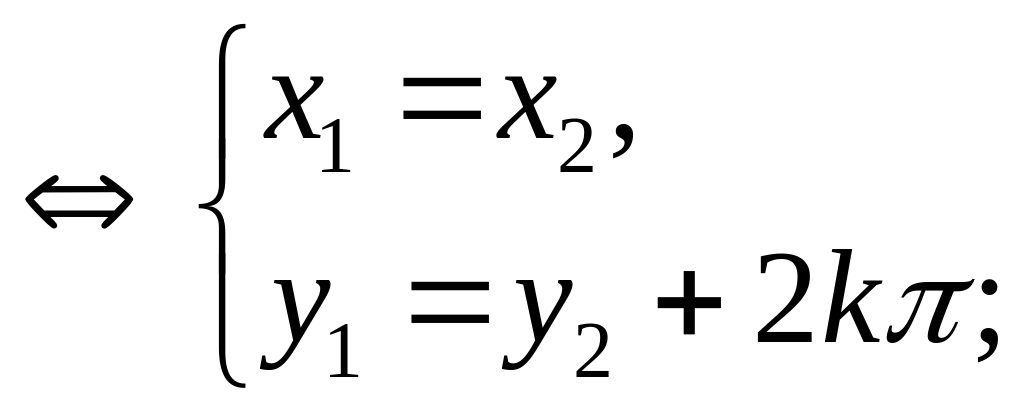
Тогда областью однолистности функции будут полоса шириной не больше , параллельная действительной оси.

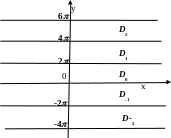
Разобьем плоскость на области однолистности: .

Если, например, , то .