5. Тригонометрические функции

Т. к. , то при сложении и вычитании соответственно получим:

, (14)

Формулы (14) – формулы Эйлера, верные .

Если , то функции , определены и являются аналитическими, следовательно они целые. При они принимают действительные значения, совпадающие соответственно с cosx и sinx. Поэтому по определению первую обозначают через cosz, а вторую – sinz и называют косинусом и синусом z.

Определение.

(15)

Формулы (15) тоже называются формулами Эйлера. Если вторую умножить на i и сложить с первой, то получим

– (16) – тоже формула Эйлера.

Свойства cosz и sinz

1 Из (15) следует cos(-z)=cosz, sin(-z)=sinz , следовательно cosz – чётная, sinz – нечётная.

2 cosz и sinz – периодические с периодом 2.

,

т. к. 2i– основной период expz.

Покажем, что 2 – основной период cosz и sinz.

Пусть w – период cosz. Следовательно, cos(z+w)=cosz.

Если , то .

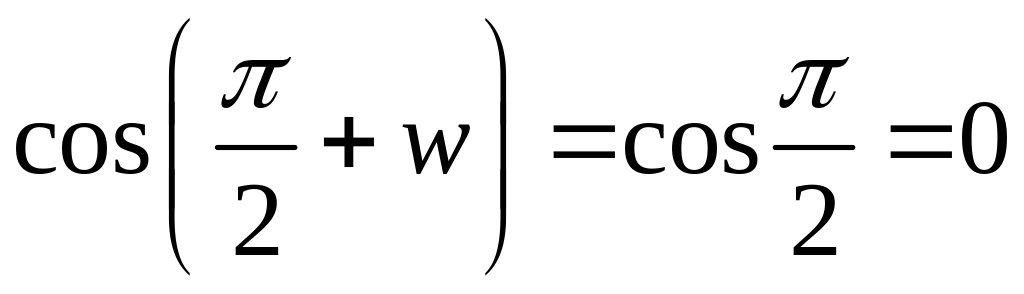Следовательно, 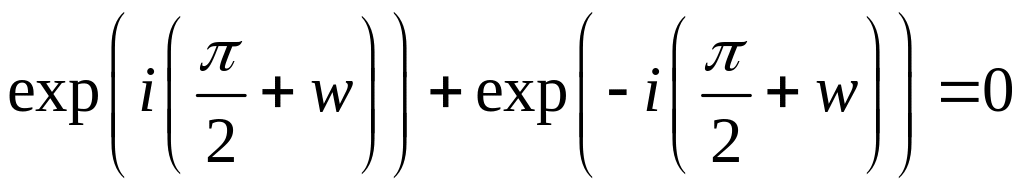(по определению cosz).

Отсюда  .

Тогда, поскольку из expz=w следует , то

. Значит w=k.

Если z=0, то 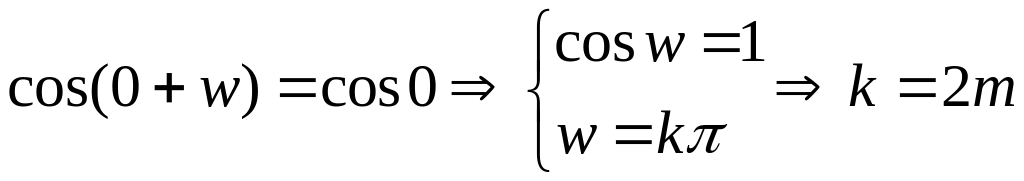(чётное число).

Значит w=2m. Следовательно, 2 – основной период функции cosz.

Для sinz аналогично.

3 Для sinz и cosz справедливы основные формулы тригонометрии:

а) 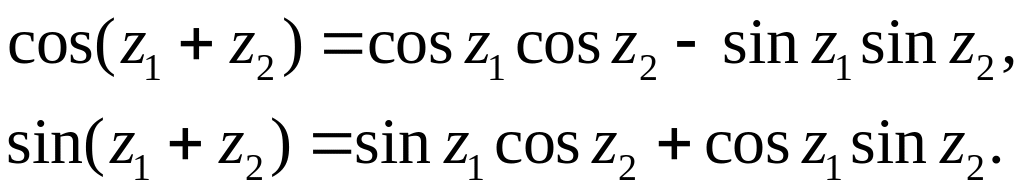(17)

Заменяя в (16) z на , получим

Следовательно,

.

Заменяя здесь z₁ и z₂ на -z₁ и -z₂ и учитывая свойство 1, получим

.

Складывая и вычитая две последних формулы, получим (17).

Формулы (17) являются основными в теории тригонометрических функций.

б) Из них следуют «формулы приведения».

Положим в (17) z₁=z, . Тогда

, .

Положим в (17) z₁=z, . Следовательно,

, .

в) Положим в 1-й из формул (17) z₁=z, z₂=-z, получим

. (18)

4 Из (18) не следует, что .

Далее покажем, что .

Пример.  Пусть z=i.

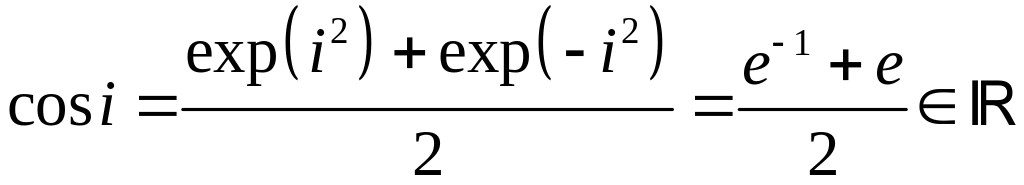
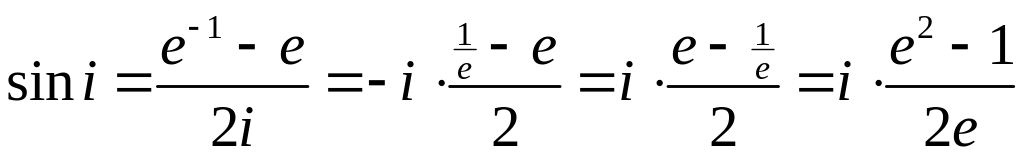– чисто мнимое.

.

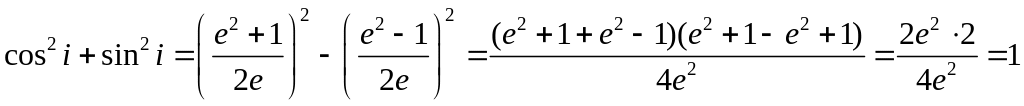Но , . 

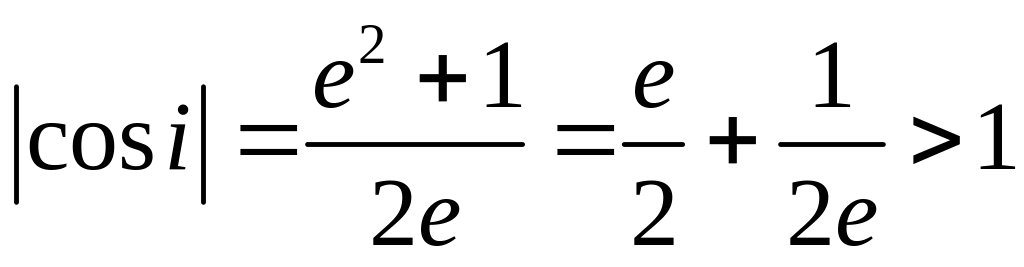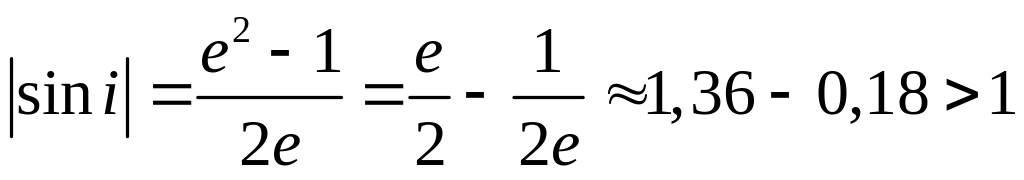5 cosz=0 при , sinz=0 при .

cosz=0

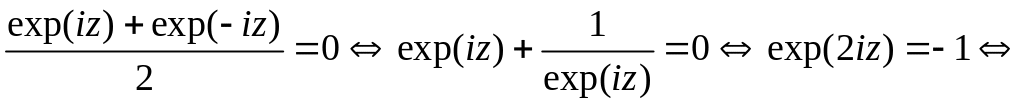
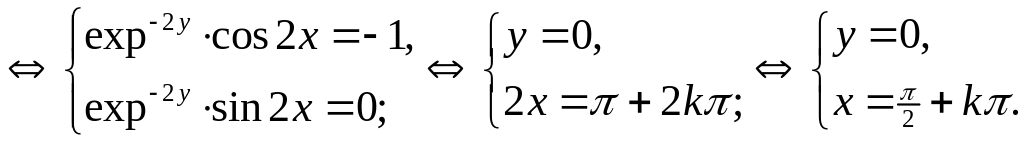
Следовательно, .

Для sinz=0 аналогично.

6 Функции cosz и sinz аналитические в .

,

.

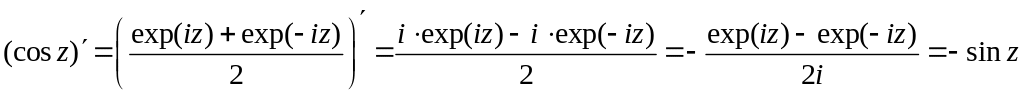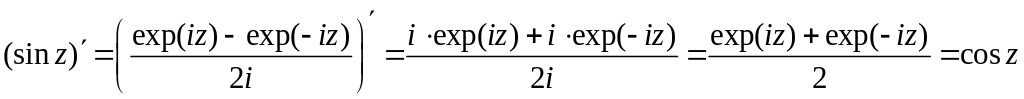Определение. .

Свойства tgz и ctgz

1. , .

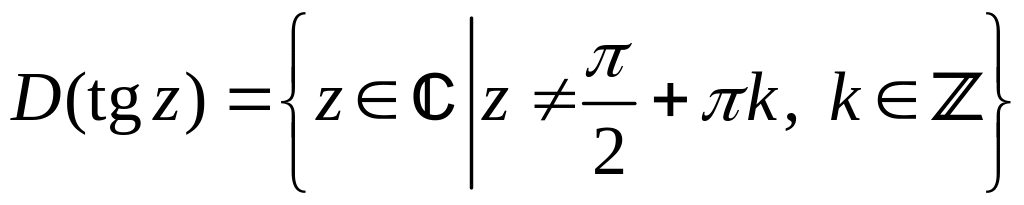2. tgz=tgx, ctgz=ctgx при .

3. tg(-z)=-tgz, ctg(-z)=-ctgz .

4. tgz и ctgz – периодические с периодом .

5. tgz и ctgz – непрерывны в своих областях определения.

6. tgz и ctgz – аналитические в своих областях определения,

, .

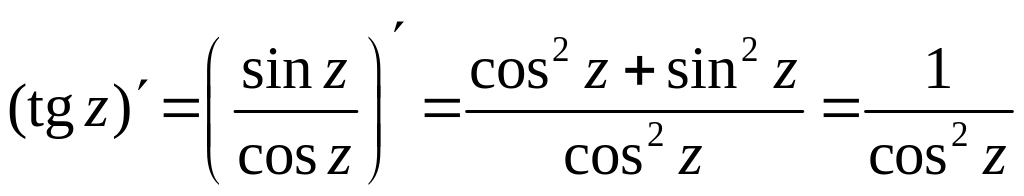7. Нули tgz совпадают с нулями sinz, нули ctgz – с нулями cosz.

8. tgz и ctgz принимают любые значения из , кроме z=i и z=-i.

.

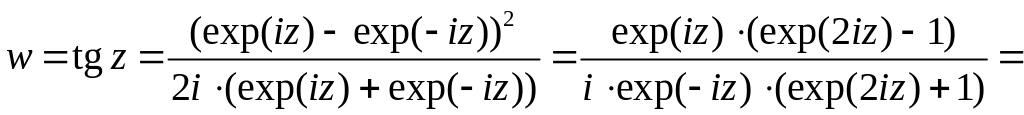
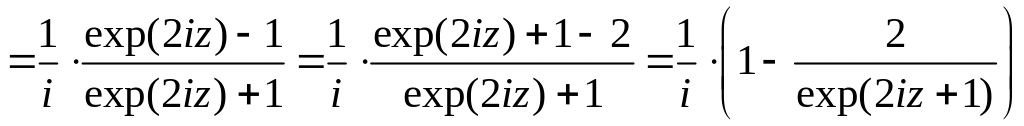Следовательно,

. (*)

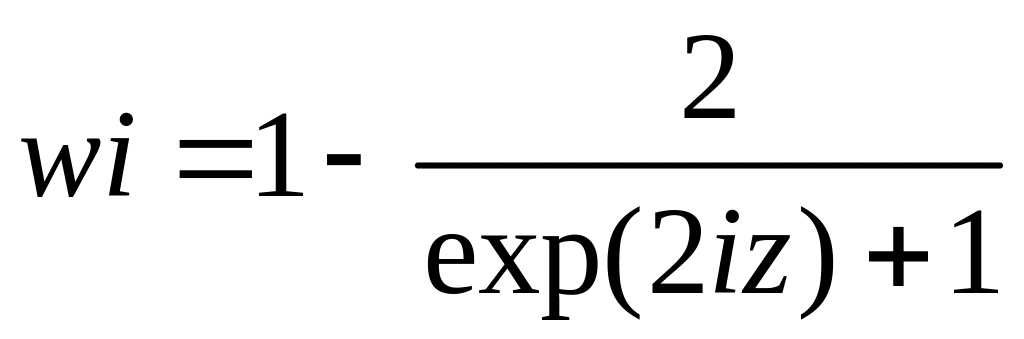
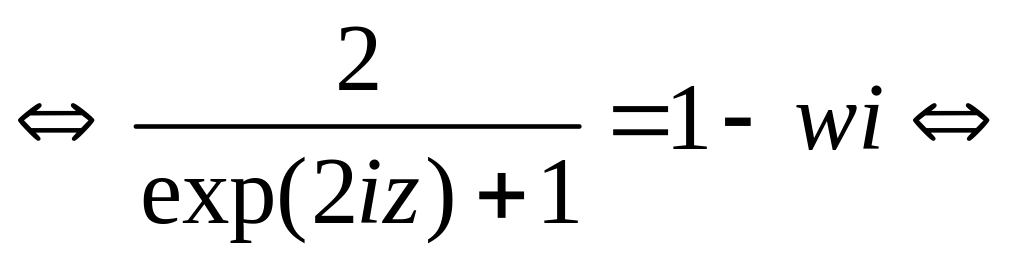
Если w=i, то (*) примет вид – нет решений;

если w=-i, то (*): 0=2 – не имеет смысла. Т. е. .

Пусть w=A ( ), тогда

.

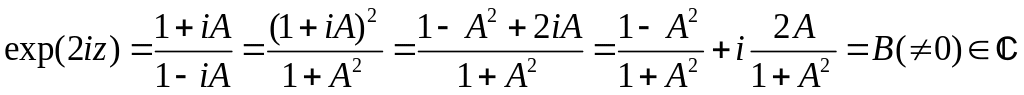Следовательно, существует точка z₀: . Т. к. , то, следовательно, существует .