3.Многочлен

К классу целых функций относятся однозначные функции, аналитические во всей конечной комплексной плоскости. Частным случаем является многочлен:

. (10)

Если n=0, то . Если n>0 и , то . Пусть - произвольное число. Тогда уравнение имеет n корней, среди которых могут быть равные (кратные корни). Следовательно, у любой точки w при отображении существует n прообразов z₁, z₂, …, z_n. Прообразами точки , служат корни уравнения , т. е. точка .

Итак, многочлен степени отображает расширенную комплексную плоскость на себя так, что каждая конечная точка образа w имеет n прообразов z₁, z₂, … , z_n.

Отображение является конформным во всех точках, за исключением точек ₁, ₂, …, _n, в которых , а также, за исключением, быть может, точки z= .

Если n=1, то - целая линейная функция – взаимно однозначное и конформное отображение в .

Рассмотрим случай n>1. Пусть , тогда z=z₀ является кратным корнем уравнения , где k 2 – кратность корня z=z₀ (k на 1 больше, чем кратность корня z=z₀ для уравнения ), а многочлен при z=z₀ . Положим , , тогда . Отсюда

. (11)

Пусть L: z=(t) - кривая, проходящая через точку z₀ (т.е. z₀=(t₀)) и имеющая в точке z₀ касательную с углом наклона

(12)

к действительной оси.

- образ кривой L при отображении .

Так как , то мы непосредственно не можем сказать, существует ли касательная к  в точке .

Рассмотрим секущую, проходящую через точку w₀, ww₀. При t>t₀

,

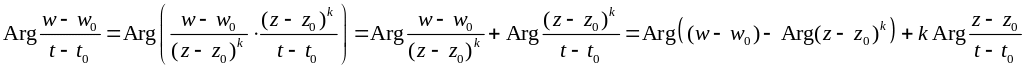т.к. . Учитывая (11), (12), получим

. Следовательно, касательная к  в точке существует, и .

Пусть , - кривые, проходящие через точку z₀ и образующие в ней угол .

.

Тогда образы этих кривых ₁ и ₂ проходят через точку и образуют в ней угол:

.

Следовательно, при отображении все углы с вершинами в точках, в которых , изменяяются, а именно, увеличиваются в число раз, равное кратности соответствующего корня уравнения .

Покажем, что в точке отображение при n>1 тоже неконформно.

Пусть L₁ и L₂- две кривые, проходящие через точку , - угол между ними.

₁ и ₂- их образы при отображении , проходящие через точку .

При отображении кривые L₁ и L₂ переходят в L₁ и L₂, точка - в точку =0 и угол между ними в точке =0 равен  (по определению угла в точке ).

Точка =0 является нулём (n-1)-го порядка производной многочлена

, , .

При отображении точка =0 переходит в точку w^*=0, кривые и - в кривые и . Угол между и в точке w^*=0 будет равен n (по доказанному выше). При отображении точка w^*=0 переходит в точку , кривые и в кривые и , и угол между ними будет n.

Итак, угол с вершиной в бесконечно удалённой точке при отображении увеличивается в n раз.