2. Дробно-линейная функция

Рассмотрим функцию вида

, (2)

где a,b,c,d- комплексные числа.

Если , то получаем -линейную функцию.

Если , выделим в дроби целую часть

.

Если ,то получаем, что . В дальнейшем будем считать, что , .

Определение. Функция вида (2), где a, b, c, d - комплексные числа, такие что , , называется дробно-линейной.

Свойства дробно-линейного преобразования

1 Конформность

.

существует во всех конечных точках комплексной плоскости, кроме точки и 0 (т.к. ). Функция является аналитической во всех конечных точках плоскости, кроме . Следовательно, отображение является конформным во всех конечных точках к плоскости, кроме .

Пусть - произвольная точка к плоскости

.

Тогда касательные к кривым, проходящим через эту точку повернутся на один и тот же угол, равный . Следовательно, угол изменяется от точки к точке.

, т.е он сохраняет постоянное значение для точек каждого из прямолинейных лучей, входящих из точки .

К оэффициент растяжения в точке равен и тоже меняется от точки к точке. , т.е он сохраняет постоянные значения для точек окружностей с центром в точке . , - изометрическая окружность дробно-линейного преобразования.

внутри , , вне , .

Дополним определение функции , положив ,

т.к. , .

Таким образом, функция определена на .

Дадим понятие угла с вершиной в бесконечно удаленной точке.

Определение. Любые две кривые и , проходящие через точку , образуют в ней угол ,если образы этих кривых и при отображении образуют в точке О(0,0) угол .

Покажем, что отображение является конформным в точке .

Пусть две кривые и образуют угол с вершиной в точке . Т.к. , то образы их и проходят через точку . По определению угол между и должен равняться углу между их образами и при отображении . Это тоже дробно-линейное отображение и, следовательно, оно конформно в точке . , значит, кривые и образуют в точке угол . Следовательно, и образуют в точке угол . А значит, отображение конформно в точке .

Покажем, что оно конформно и в точке .

Рассмотрим обратную функцию к . Из уравнения

-

тоже дробно-линейное отображение.

Обозначим . .

конформно в точке . Т.к. , то . Следовательно, конформно в точке .

Итак, дробно-линейная функция отображает взаимно однозначно и конформно расширенную комплексную плоскость саму на себя.

2  Круговое свойство.

Частный случай . (3).

Положим , .Тогда (3) примет вид

Следовательно, отображение (3) разбивается на два отображения. Сначала точка переходит в точку 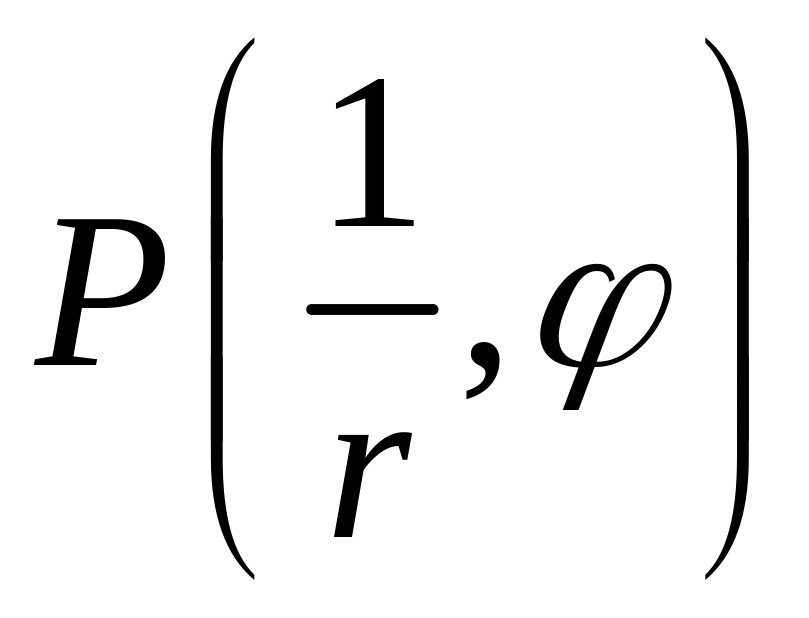.Т.к. эти точки лежат на одном луче, выходящем из начала координат и их модули связаны соотношением , то это преобразование инверсии относительно единичной окружности. Затем точка переходит в точку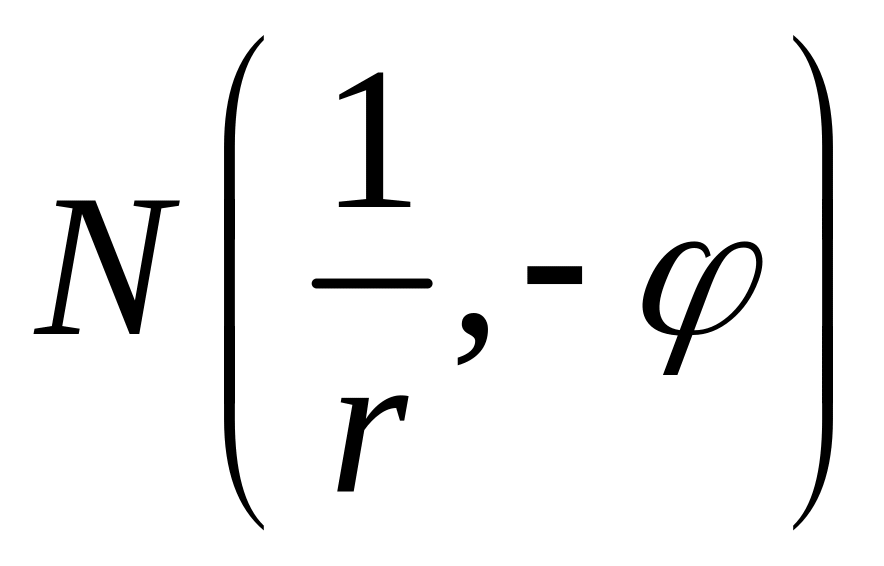 , симметричную ей относительно действительной оси.

Теорема. При отображении совокупность прямых и окружностей на комплексной плоскости переходит в себя.

Доказательство.

Уравнение для любой прямой или окружности имеет вид:

А(x²+y²)+2Bx+2Cy+D=0. (4)

При А=0 и В, С 0 одновременно это уравнение определяет прямую, при А=0 и В²+С² -AD>0 – окружность.

Заменим , , , (5)

получим .

Обозначим , тогда

. (6)

Если А=0, а Е0, то уравнение (6) определяет прямую, если А0 и , то окружность. Т.е. любая окружность или прямая на комплексной плоскости определяется уравнением (6).

Верно и обратное: уравнение вида (6) определяет прямую или окружность на комплексной плоскости. Для доказательства надо в (6) сделать замену по формулам (5). Получим (4) , которое является уравнением либо прямой, либо окружности.

При преобразовании имеем . Линия (6) перейдет в линию:

. (7)

Уравнение (7) имеет тот же вид, что и (6), с заменой A на D, D на А, E на . Следовательно, при D=0 – это уравнение прямой, а при - уравнение окружности.

Следствие. Образом прямой или окружности при дробно-линейном отображении w=L(z) является прямая или окружность, (причем образом прямой может быть как окружность, так и прямая, и образом окружности – как прямая, так и окружность).

Доказательство.

.

Следовательно, w=L(z) является композицией трех отображений: t=cz+d, , w=kq+l, где , . Первое и третье - линейные отображения. Они и отображение переводят в себя совокупность прямых и окружностей.

Замечание. Несложно установить, что при отображении w=L(z) все прямые и окружности, проходящие через точку переходят в прямые плоскости (w), а все прямые или окружности, не проходящие через точку , - в окружности плоскости (w).

3 Инвариантность двойного отношения

Дробно-линейное преобразование однозначно определяется заданием трех параметров (например, если с0, то ими могут быть ). Поэтому это отображение определяется заданием образов трех точек. Выведем формулу дробно-линейного преобразования.

Пусть , k=1,2,3. Пусть . Образуем разности

,

, ,

, .

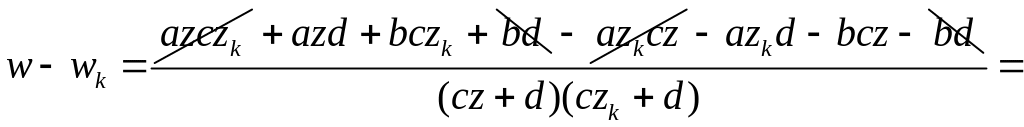
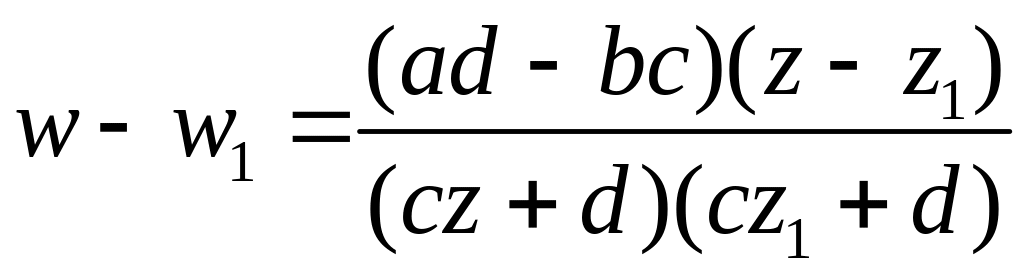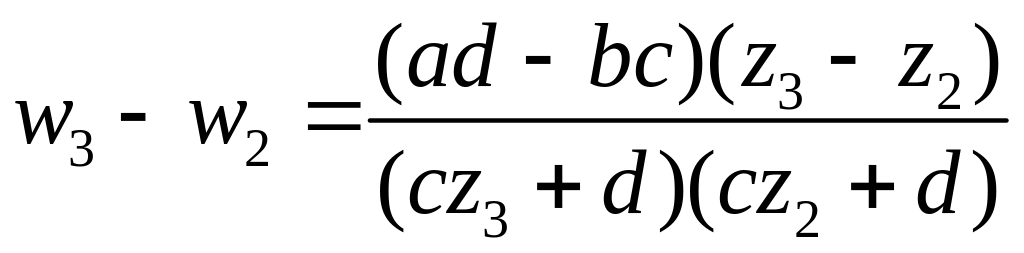Разделим почленно первое уравнение на второе и третье и на четвертое.

,

.

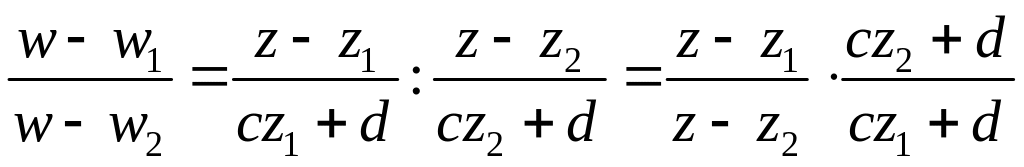Разделим теперь снова первое уравнение на второе:

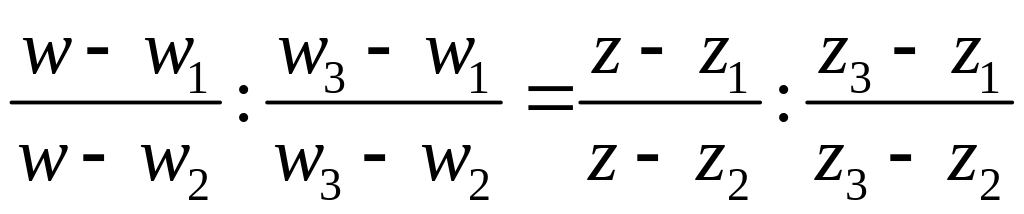. (8)

Это и есть искомое линейное преобразование.

Т.к. за z₁, z₂, z₃, z и w₁, w₂, w₃, w могут быть приняты любые четверки точек, соответствующие друг другу при дробно-линейном преобразовании, то (8) выражает следующее свойство:

отношение сохраняется при дробно-линейном отображении, т.е является его инвариантом. Это отношение называется двойным отношением четырех точек.

4 Сохранение симметрии

Если точки z₁ и z₂ симметричны относительно некоторой прямой или окружности , то при любом дробно-линейном отображении w=L(z) их образы w₁ и w₂ будут симметричны относительно образа : .

В случае, когда  - окружность, преобразование называют инверсией.

5 Принцип соответствия обхода границ (отображение областей, ограниченных прямыми или окружностями)

Е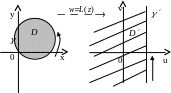 сли при дробно-линейном отображении прямая или окружность  переходит в прямую или окружность  ,то область D, которую ограничивает , преобразуется в одну из двух областей, которые ограничивает . При этом имеет место принцип соответствия обхода границ: если при каком-то обходе линии  область D оказывается слева (справа), то при соответствующем обходе линии  область D тоже должна оказаться слева (справа).