6.2 Понятие о статических и динамических силах

На рис. 4.2 представлен ротор массой m, выполненный в виде диска, насаженного на вал, который вращается в подшипниках А и В с постоянной угловой скоростью W. Для простоты рассуждения допускается, что главная центральная ось инерции параллельна оси вращения ротора и отстоит от нее на расстоянии ps Пусть к ротору приложены силы Р_] и Р₂, постоянные по величине и направлению, и пара сил с моментом M(рис. 4.2). Требуется определить давление подшипников на ротор.

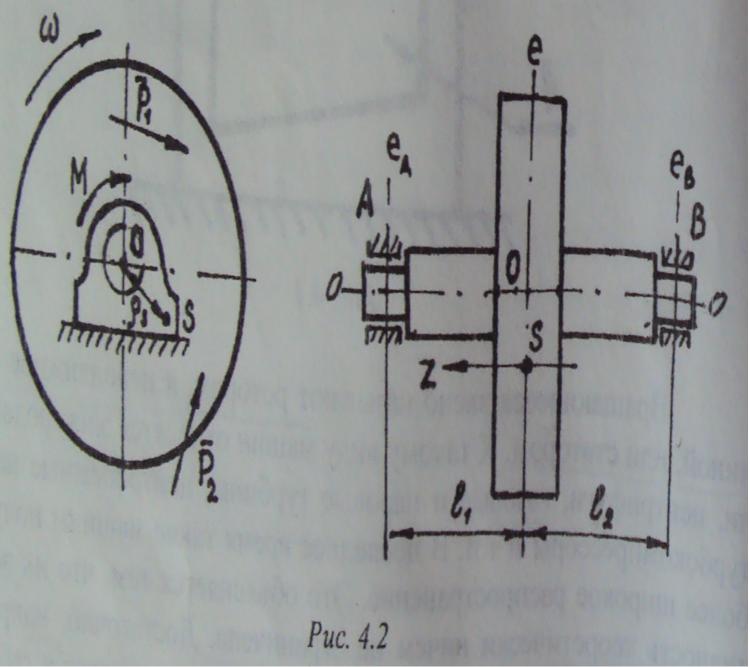
Силы Р, и Р₂ переносят в точку О (рис. 4.3). При этом в плоскости е появляются соответствующие пары сил с моментами М, = М(Р,) и М₂ = М(Р2). В плоскостях еa_А eb_в, проходящих через середины подшипников, возникают реакции Q1a и Q1b Действие которых заменяется одной неизвестной силой (Q1, приложенной к точке О. Причем направления сил Q1a Q1b и Q1 показаны условно, а плоскости ea еb и е перпендикулярны оси вращения.

В результате на ротор будут действовать система сходящихся сил P1, p2 и Q1 система пар сил с моментами M1,M2,M3

Силы, приложенные в центре О, можно заменить одной равнодействующей:

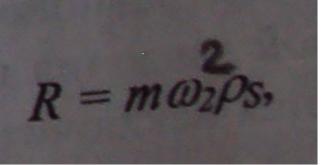
где = - представляет собой нормальное составляющее ускорения центра масс, которое направляется по ps к центру вращения. Такое же направление будет иметь и R.

Согласно теореме о сложении пар сил, все моменты можно заменить результирующим моментом:

Поскольку равнодействующая пересекает ось вращения, Mr=0, следовательно, и сумма моментов М1,M2,M3 равна нулю, то есть приложенные пары сил взаимно уравновешиваются, поэтому их можно исключить из рассмотрения.

На основании свойств равнодействующей:

Графическое решение данного векторного уравнения приведи но на рис. 4.4, что позволяет определить величину и направлений силы Q1

Для нахождения сил давления на ротор со стороны каждого подшипника достаточноQ1 _] разложить на две параллельные силы, определяемые из соотношений

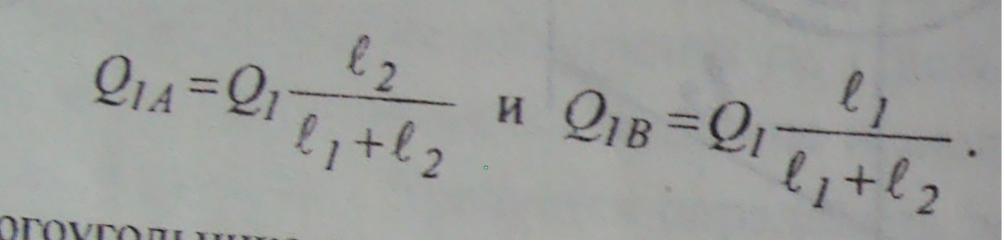
Из многоугольника сил на рис. 4.4 можно заметить, что в нега; входят две категории сил: силы, которые не зависят от вращения ротора(P1 и P2) и силы, обусловленные вращением ротора (сила R), по- этому силу Q1 - давление подшипника на ротор раскладывают на две составляющие:Q1c и R. Составляющие Q1c, Р₁ и Р₂ образуют треугольник взаимно уравновешивающихся сил, поэтому Q1c можно определить, пользуясь условиями равновесия сил. Эту составляющую называют статической силой давления подшипников на ротор. Итак! статическая сила определяется исключительно приложенными к роте ру силами, не зависящими от характера движения ротора. Она всегда остается постоянной и по величине, и по направлению. К статической силе можно отнести вес ротора, давление между зубьями в зубчатой передаче, силу натяжения ремня в ременной передаче и другое. Чтобы

получил, статическую силу давления на ротор каждого подшипника в отдельности, необходимо Q1c разложить на две параллельные составляющие (рис. 4.5):

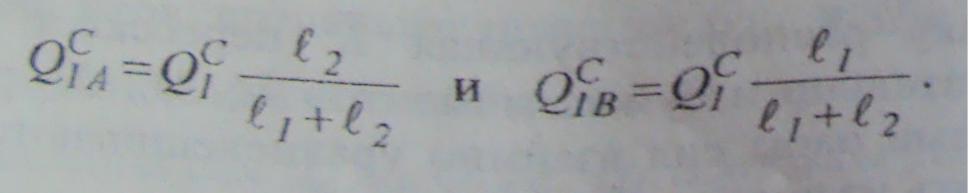
В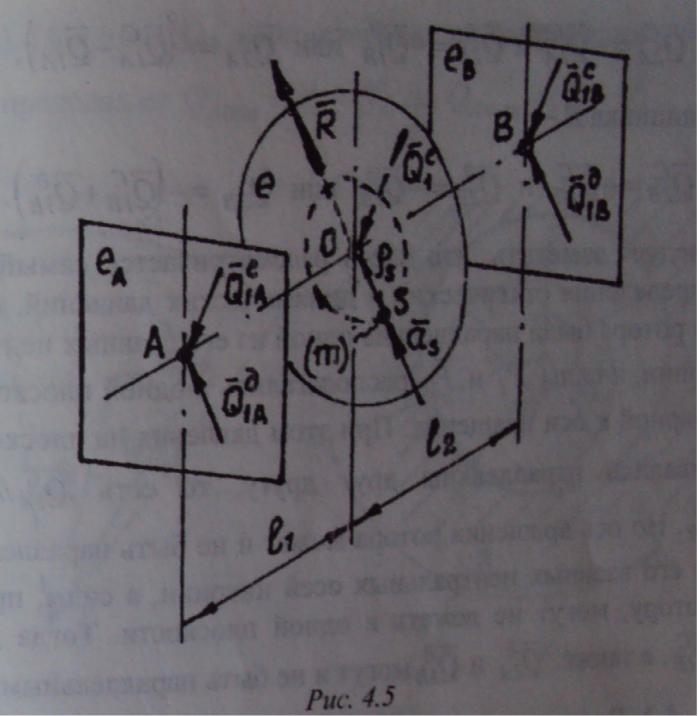 торая составляющая - R =mw2^2ps - пропорциональна ускорению центра масс. Если это ускорение сделать равным нулю, остановить ротор или совместить ось вращения с его главной центральной осью инерции, то и R окажется равной нулю. При вращении ротора с Угловой скоростью w вектор R вращается вместе с ротором с той же угловой скоростью. Вызванная неуравновешенностью ротора составляющая

н азывается силой динамического давления подшипников на ротор. Она для каждого подшипника в отдельноcти(рис. 4-5) будет находиться но формулам

Давления ротора на подшипники численно равны давлениям подшипников на ротор но направлены в противоположную сторону, следует, что для подшипника А имеет место соотношение

С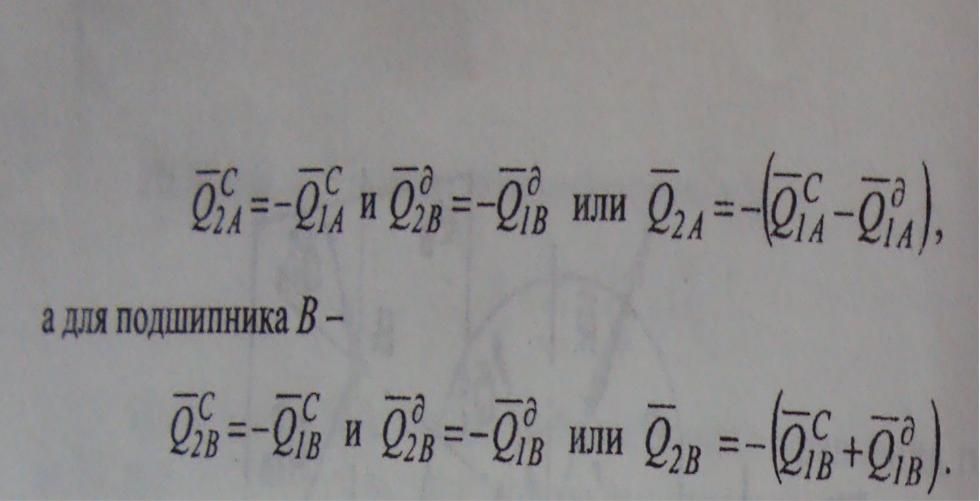 ледует заметить, что здесь рассматривается самый простой случай определения статических и динамических давлений, когда ось вращения ротора была параллельна одной из его главных центральной осей инерции, а силы Р1 и Р₂ располагались в одной плоскости, перпендикулярной к оси вращения. При этом давления на плоскостях е_А | е_в оказывались параллельны друг другу, то есть

ось вращения ротора может и не быть параллельной ни одной из его главных центральных осей инерции, а силы, приложенные к ротору, могут не лежать в одной плоскости. Тогда давление

могут и не быть параллельными 4.2. Режимы движения цапфы в подшипнике

Для определения полного давления подшипника на цапфу ротора необходимо статическое давление геометрически сложить с динамическим:

В зависимости от значений Q^эи Q^е возможны три случая, которые приводятся ниже для подшипника А.

Вектор Q^еa статического давления остается неизменным а вектор Q^эа динамического давления вращается вместе с ротором с той I же угловой скоростью, что и ротор. Поэтому вектор Qa представляющий их геометрическую сумму, будет поворачиваться вокруг точки р в пределах некоторого угла альфа то в одну, то другую сторону (рис. 4.6а). При этом Qa изменяется как по направлению, так и по величине в пределах от

У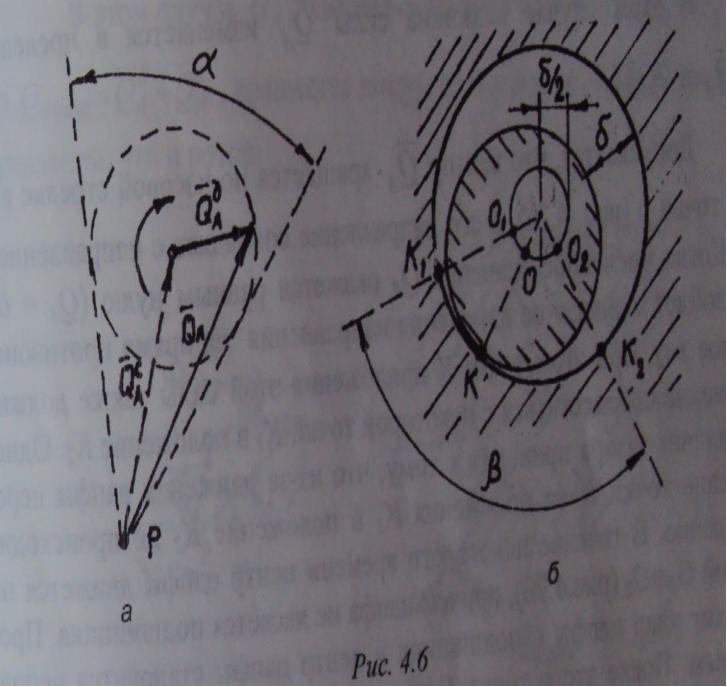 читывая трение скольжения при движении цапфы в подшипниках, силу Q_А следует направить по касательной к кругу трения (см. 2.1.2). Тогда вектор Qa будет совершать колебательное движение

в пределах угла альфа, а точка К касания цапфы с подшипником - по определенной дуге. Однако эти рассуждения справедливы для случая, когда отсутствуем зазор между цапфой и подшипником. В действительности же диаметр цапфы всегда меньше внутреннего диаметра подшипника на величину б (рис. 4.66), поэтому перемещение точки К влечет за собою к перемещение центра О цапфы. При этом точка К будет двигаться по дуге К1КК2 а точка О - по дуге О1ОО2 радиуса б/2. Причем угол Бэта который стягивается этими дугами, отличается от, угла альфа. Этот режим называется режимом колебательного движения, или первым режимом. При таком движении подшипник изнашивается в зоне соприкосновения с цапфой, то есть с одной стороны, а цапфа - кругом,