5.3. Силовой анализ кулачковых механизмов

Силовой анализ кулачковых механизмов заключается в определении сил взаимодействия между его звеньями. Знание о величинах и характере действия этих сил необходимо для проведения прочностных расчетов деталей, для определения энергозатрат, необходимых при работе механизма, и для определения КПД. Методика и последовательность силового расчета кулачковых механизмов в основном зависит от их конструктивных особенностей и может быть выполнена! если известны геометрические и конструктивные размеры механизма, скорости и ускорения толкателя, массы звеньев, а также моменты! инерции масс звеньев, совершающих вращательные движения.

53.1. Определение сил в кулачковом механизме с роликом и толкателем

На рис. 5.9а представлен кулачковый механизм с толкателем, 1 оканчивающийся роликом. Необходимо определить силы, действующие на толкатель в заданном его положении.

В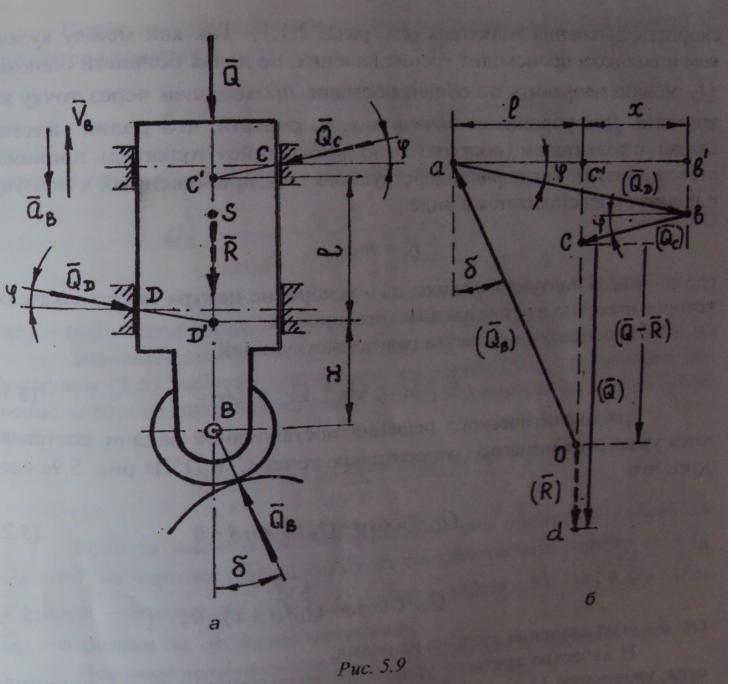 водятся следующие обозначения сил: Q- известная сила, прижимающая толкатель к кулачку, направленная вдоль прямой C'D', по которой двигается общий центр масс S толкателя и ролика; Q_С

Q_D- силы реакции станины; Q_B сила давления кулачка на ролик. Силы Q_{С И}Q_D- и можно считать приложенными в серединах поверхностей соприкосновения толкателя с опорой (в точках D и С). Эти силы отклоняются от общей нормали к поверхностям опор на угол трения фи, не превышающий угол в момент начала скольжения, против скорости движения толкателя (см. разд. 2.1.1). Так как между кулачком и роликом происходит трение качения, не делая большой ошибки, Q_В можно направить по общей нормали, проходящей через точку их контакта. Дня упрощения задачи можно считать, что ролик жестко связан с толкателем (поступательно движущийся толкатель принимается за ползун). Тогда равнодействующая сил, приложенных к ползуну и ролику, представляется в виде

г де т - масса ползуна и ролика, Aв - ускорение центра масс толкателя, которое известно из кинематического анализа.

На основании свойства равнодействующей

(5.1)

Для аналитического решения поставленной задачи составляются уравнения моментов относительно точек С'иD' рис. 5.9а следует, что

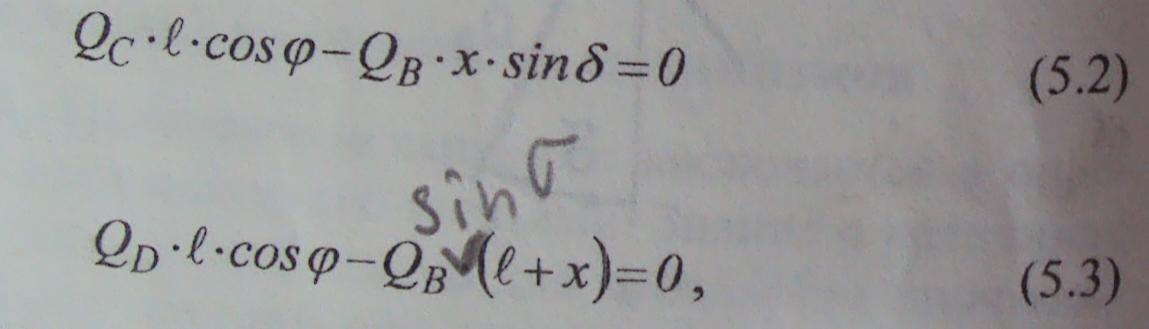
где б- угол давления кулачка на ролик.

В качестве третьего уравнения, связывающие силы, принимается уравнение (5Л), спроектированное по направлению ускорения

а_в ,то есть

П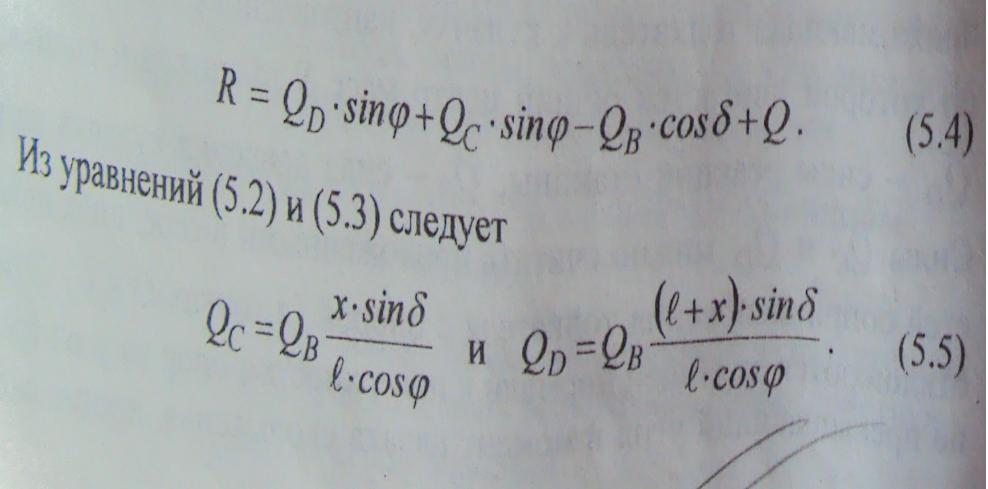 осле подстановки последнего соотношения в формулу (5.4), получится уравнение

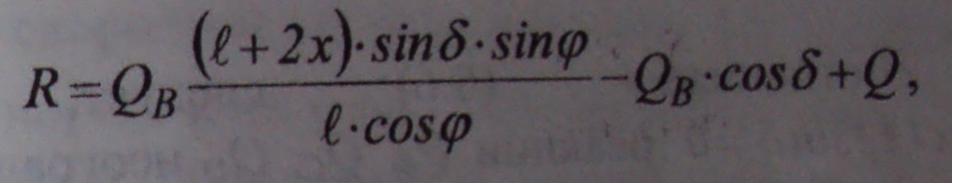решение которого приводит к определению Qb

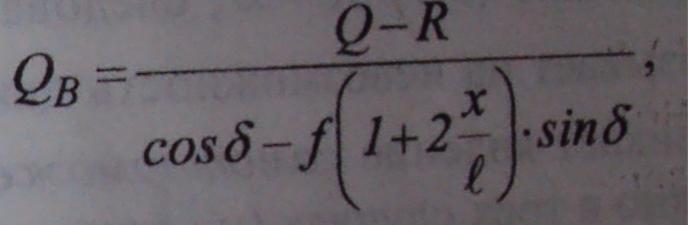
где f=tg фи - коэффициент трения скольжения.

Значения сил Qc и Qdпри известном Qb можно находить по формулам (5.5) либо из векторного уравнения (5.1), графическое решение которого показано на рис. 5.96. Из выражений (5.2) и (5.3) следует, что

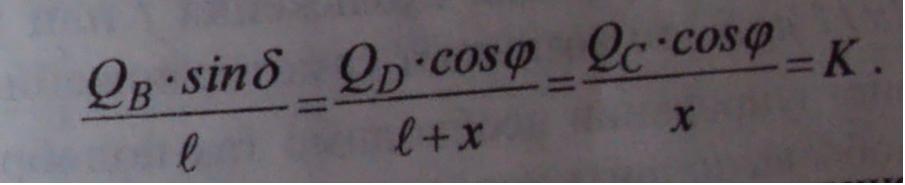Если за масштабный коэффициент сил принять К (н/мм), то Qb*sin(b)_в на чертеже (рис. 5.96) будет соответствовать отрезку ас'=l'; Qd*cos(Фи) - отрезку ab'=l+x Qc*cos(фи)-отрезку b'c'=x, а Qc,Qb,Qd - отрезкам оа, аЬ, Ьс соответственно.

Искомые величины сил Qd,Qc,Qb находят из соотношений

Qв = Коа; Qd = КаЬ; Qс=Kdс, а силы Q и R на чертеже пропорциональны отрезкам cd и od

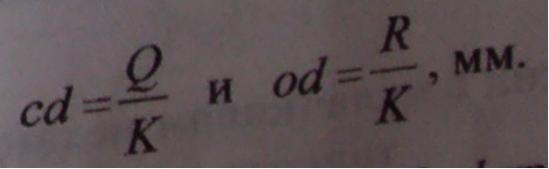
Следовательно, многоугольник оаbcd представляет собой план сил, выполненных в масштабе

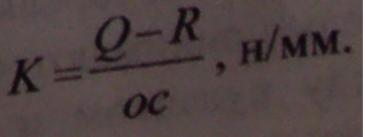
В случае когда R будет иметь противоположное направление,

Из соотношения (5.6) следует, что при

реакции Qb,Qc,Qd неограниченно возрастают. Такая же картина наблюдается, когда точки О и С (рис, 5.96) совпадут и согласно выражению (5.7) К=оо, следовательно, Qb=оо, Qc=оо, Qd=oo. Это указывает на невозможность движения толкателя, то есть при этом возникает явление самоторможения механизма. Подобное явление возможно в трех случаях (по трем параметрам): 1

1. По углу давления б. При угле давления, удовлетворяющей условию tgб-f(1+2x/l)sinб=0 кулачковый механизм не работает,по этому при конструировании необходимо добиваться, чтобы tgб<1f(1+2х/l).

2. По коэффициенту трения скольжения f или углу трения W Если f<1/(1+2х/1)tgб, то возникает самоторможение. Отсюда следует, что при конструировании необходимо так подобрать материал! трущихся тел, чтобы выполнить условие f<1/(1+2х/l)tgб.

3. По геометрическим размерам х и I. При увеличении х/l до величины х/l=(1-f-tgб)/(2f tgб) сила Qb следовательно, и сил Qd и Qc будут бесконечно большими. Из этого следует, что кулачковый механизм будет работоспособным только при х/l<(1-f tgб)/(2f Tgб).

Таким образом, при конструировании кулачковых механизмом нужно стремиться к уменьшению угла давления б, угла трения скольжения фи и x/l.