
- •6.4 Режимы движения цапфы в подшипнике
- •6.5 Уравновешивание ротора
- •6.6 Статическая балансировка
- •6.7 Динамическая балансировка роторов
- •6.8 Допустимая неуравновешенность
- •7 Исследование кпм
- •7,1 1.Назначение и уст-во кпм.
- •7.2. Аналитический способ определения положения, скорости и ускорения ползуна
- •7,3 3.Индикаторная диаграмма и силы прилож. К ползуну
- •7,4. Момент инерции вращающегося звена и маховика
- •5.Степень неравномерности колеб. Кривошипа в кпм.
6.5 Уравновешивание ротора
Ротор считается неуравновешенным, если главная центральная ось инерции не совпадает с осью его вращения, иначе говоря, неуравновешенность характеризуется ассиметричным расположением его массы относительно оси вращения.
Цель уравновешивания- совмещение главной центральной оси инерции с осью его вращения. Уравновесить ротор - значит устранить асимметрию массы ротора по всему объему относительно оси вращения. Это достигается с помощью уравновешивающих грузов - противовесов. Вопрос сводится к тому, где и сколько таких грузов следует установить, чтобы ось вращения стала одновременно и главной центральной осью инерции.
Обычно противовесу придают такую форму, при которой одна из главных центральных осей инерции становится параллельной оси вращения, а сами «плоскости противовесов» назначаются конструктором в зависимости от конструктивных особенностей ротора.
Пусть требуется уравновесить ротор определенной массы, вращающийся на подшипниках А и В с постоянной угловой скоростью w (рис. 4.9).
Можно представить, что тела I и 111 вращаются вокруг своих
г лавных
центральных осей инерции, следовательно,
не вызывают появления динамических
давлений. Центр масс
S
тела
11 находится на расстоянии
ps
от оси вращения. Тогда при движении
ротора в подшипниках А и
В возникают динамические
силы:
лавных
центральных осей инерции, следовательно,
не вызывают появления динамических
давлений. Центр масс
S
тела
11 находится на расстоянии
ps
от оси вращения. Тогда при движении
ротора в подшипниках А и
В возникают динамические
силы:

Назначают на роторе две произвольные плоскости е' и е", отстоящие от оси е тела II на расстоянии l1 и l2, которые мысленно переносят подшипники А и В. При этом в этих мнимых (фиктивных) подшипниках А' и В' также появляются динамические давления:
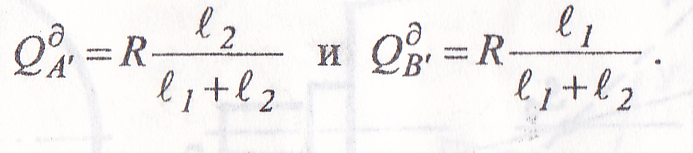
Следовательно, для их уравновешивания в плоскостях е' и е" необходимо ввести такие противовесы Q1д и Q2д ,чтобы выполнялись условия
![]()
Если обозначить массы противовесов через m1 и т2, а расстояние центров масс Si и S2 до оси вращения через p1и р2, то согласно соотношению R=mw2ps можно из (4.3) установить, что

Таким образом, для уравновешивания любого жесткого ротора необходимо и достаточно установить два противовеса. Плоскости, в которых устанавливаются противовесы, называются плоскостями уравновешивания или коррекции. Неуравновешенность любого жесткого ротора можно представить двумя силами Q1д и Q2д, расположенными в произвольных плоскостях е' и е", перпендикулярных оси вращения ротора.
6.6 Статическая балансировка
Статическая балансировка может производиться на горизонтальных линейках, в центрах, на вращающихся роликах, на аэростатических опорах. Так как принципиально это одно и то же, можно ограничиться рассмотрением статической балансировки на горизонтальных стальных линейках.
Ротор кладут на горизонтальные стальные линейки так, чтобы он опирался на них своими цапфами (рис. 4.10).

Если центр масс ротора S не лежит на оси вращения, то под действием сил G (вес ротора) и Q (давление линеек) ротор будет перекатываться и через некоторое время займет наинизшее положение
(S). Тогда в вертикальной плоскости, проходящей через ось вращения OO, к ротору прикрепляется противовес G1 Вес противовеса подбирают так, чтобы ротор мог оставаться в покое в любом положении (безразличное равновесие).
Установить противовес так, чтобы общий
центр масс So ротора и
противовеса находился на оси вращения,
не удается. Действительно, при качении
цапфы по горизонтальной линейке из-за
наличия трения качения создается момент
трения (рис. 4.11), препятствующий качению:
![]()
где к - плечо трения качения, Q - давление линейки на цапфу.
Если смещение рs центра масс S не больше плеча трения качения k, то балансируемый ротор не обнаружит стремления к качению, так как сила тяжести G уравновесится давлением линеек Q , и создастся впечатление уравновешенности.
Если даже общий центр массы So лежит на оси вращения (рис. 4.12), главная центральная ось инерции может не совпадать с осью вращения, а будет образовывать угол альфа между осями. В результате этого при вращении статически отбалансированного ротора возникают динамические давления QAд и Ов п подшипников на цапфы, образующие пару сил с моментом
![]()
где Jy и Jz — моменты инерции относительно осей Y и Z соответственно.
Динамические силы давления подшипников на ротор определяются по формуле
Qд a * Q дb =M rr/L.
О сновным
недостатком статической балансировки
является низкая точность уравновешивания,
и поэтому допустима лишь для
малоответственных и тихоходных, а также
доскообразных роторов.
сновным
недостатком статической балансировки
является низкая точность уравновешивания,
и поэтому допустима лишь для
малоответственных и тихоходных, а также
доскообразных роторов.
