19. Обобщенный закон Ома. Сторонние силы, эдс. Закон Ома для замкнутой цепи.

Закон Ома для замкнутой цепи выводится из закона Джоуля-Ленца:

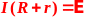
Электродвижущая сила ЭДС — отношение работы сторонних сил к вел-не перемещаемого заряда Сторонние силы – это сиды не электростатической природы.

Устройства, обеспечивающие возникновение и действие сторонних сил, называют источниками тока.

Количественной характеристикой поля сторонних сил является напряженность :

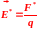
Отношение работы сторонних сил A^* к величине перемещаемого заряда называется электродвижущей силой источника тока.

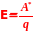
20. Работа и мощность тока. Закон Джоуля-Ленца в интегральной и локальной форме.

Закон Джоуля — Ленца:

При протекании тока проводник нагревается. Пусть за время t в нем выделяется количество тепла Q.

Величину, равную теплоте, выделившейся в единицу времени, называют тепловой мощностью тока:

количество теплоты, выделяемой в цепи:

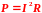
т епловая мощность тока:

Используя закон Ома, можно записать:

Удельная тепловая мощность P_уд определяет количество теплоты, которое выделяется в единице объема проводника за единицу времени:

З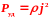 апись Закона Джоуля – Ленца в локальной форме:

Работа = Количеству теплоты

21. Классическая теория электропроводности (кэт). Вывод законов Ома и Джоуля-Ленца в рамках кэт. Электрическая проводимость. Формула Друде-Лоренца.

Согласно теории Друде-Лоренца свободные электроны металлического проводника представляют собой идеальный газ. Частицы этого газа участвуют в хаотическом тепловом движении и испытывают неупругие столкновения с ионами, образующими кристаллическую решетку.

Среднее время между двумя последовательными соударениями электрона с решеткой называют средним временем свободного пробега , а расстояние, которое проходит электрон за это время  средней длиной свободного пробега .

З акон Ома в электронной теории:

Запишем формулу для плотности тока:

где n – концентрация электронов.

Средняя дрейфовая скорость равна половине максимальной:

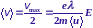
Видим, что дрейфовая скорость линейно зависит от напряженности. Коэффициент пропорциональности между ними называют подвижностью. Это понятие может относиться не только к электронам, но и к другим носителям заряда.

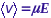
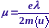
- подвижность

Выполняем подстановку <v> в формулу для плотности тока и получаем:

Видим, что электронная теория позволила получить закон Ома и вычислить удельную электрическую проводимость.

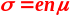- это знаменитая формула Друдэ-Лорэнца.

22. Электропроводность твердых тел. Проводники, полупроводники и диэлектрики. Температурная зависимость электропроводности твердых тел.

Энергия электрона в атоме может принимать только дискретные значения. Если какая то зона при Т=0 заполнена частично, то это проводник. Типичные полупроводники – это эл-ты 4й группы табл менделеева (кремний, германий).Концентрация электронов в зоне проводимости идырок в валентной зоне в собственном полупроводнике – 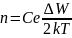. Полупроводники n-типа (электронные) получают путём введение в собственный полу/пров-ик примеси. Примесь, отдающую электроны наз-ют донорной. Полупроводник р-типа (дырочный) получают путём добавления в собств проводник примеси.