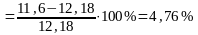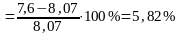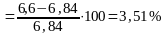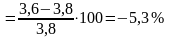- •Лабораторная работа № 7. Изгиб с кручением ломаного бруса круглого и прямоугольного сечения……………... 57
- •Лабораторная работа № 5 испытание консольной балки на косой изгиб
- •Лабораторная работа №6
- •Лабораторная работа № 7 изгиб с кручением ломаного бруса (плоской рамы) круглого и прямоугольного сечения
- •Лабораторная работа №8
- •Лабораторная работа №9
Лабораторная работа № 7 изгиб с кручением ломаного бруса (плоской рамы) круглого и прямоугольного сечения
Цель работы: Экспериментальное определение упругих прогибов плоской рамы при изгибе с кручением, проверка прочности бруса прямоугольного и круглого сечения.
Оборудование, приборы и инструменты:
- мерительная линейка, с = 1 мм;
- штангенциркуль, с = 0,1 мм;
- набор грузов весом 2 кг;
- настольная установка плоской рамы (2 варианта сечений);
- угольник мерительный, с = 1 мм
Материал бруса - сталь 45 закалённая.
Схема установки плоской рамы
К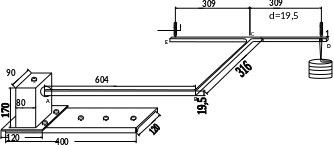 онструктивная
и расчётная схема плоской рамы для двух
вариантов исполнения сечения коренного
участка (прямоугольное и круглое)
представлена на рисунках 45 и 46.
онструктивная
и расчётная схема плоской рамы для двух
вариантов исполнения сечения коренного
участка (прямоугольное и круглое)
представлена на рисунках 45 и 46.
Рисунок 45 - Схема установки плоской рамы при пространственном нагружении
а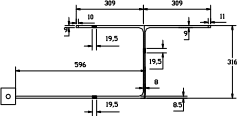 )
)
б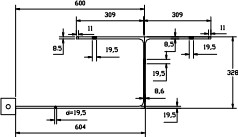 )
)
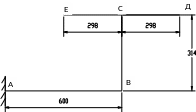
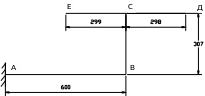
Рисунок 46 - Конструктивная и расчётная схема плоской рамы.
а) прямоугольное сечение на всех участках; б) круглое сечение на коренном участке
По результатам геометрических обмеров конструктивных схем составим таблицу исходных размеров и расчётных геометрических характеристик (табл.20)
Таблица 20 - Таблица геометрических характеристик участков плоской рамы
Тип рамы |
Участок рамы |
l, мм |
b, мм |
h, мм |
d, мм |
|
|
|
|
|
γ |
|
|
Рисунок59а |
AB BC CD CE |
600 307 298 299 |
8.5 8 9 9 |
19.5 19.5 19.5 19.5 |
─ ─ ─ ─ |
2.294 2.44 2.17 2.17 |
0.5387 0.507 0.57040.5704 |
0.5252 0.4943 0.5561 0.5561 |
0.3583 0.3218 ─ ─ |
0.2897 0.2472 ─ ─ |
0.7826 0.7765 ─ ─ |
4.53 5.0 ─ ─ |
105 98.9 111.2 111.2 |
Рисунок59б |
AB BC CD CE |
600 314 298 298 |
─ 8.6 8.5 8.6 |
─ 19.5 19.5 19.5 |
19.5 ─ ─ ─ |
─ 2.27 2.29 2.27 |
0.728 0.545 0.5387 0.545 |
0.7098 0.5314 0.5252 0.5314 |
1.4559 0.3665 ─ ─ |
1.4195 0.2991 ─ ─ |
─ 0.7837 ─ ─ |
1.25 4.441 ─ ─ |
142 106.3 105 106.3 |
*Для круглого сечения использованы следующие формулы:
Wx = πd3/32, Jx = πd4/64, Wk = πd3/16, Jk = πd4/32.
Теоретический расчёт прогибов рамы при изгибе с кручением
Прогибы определяем в двух точках D и E по концам рамы для двух схем нагружения силой P в этих же точках, по универсальной формуле Мора-Максвелла.
Существенными являются деформации изгиба и кручения. Эпюры изгибающих и крутящих моментов в плоской раме, выраженные через геометрический параметр «а», представлены в общем виде на рисунке 63 для двух схем загружения.
Выполним расчет прогибов рамы (рисунок 62 а).
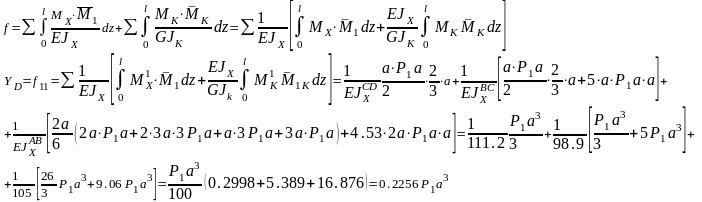
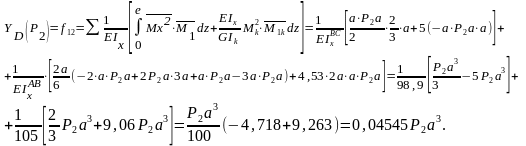 Для
варианта рамы с круглым сечением на
участке АВ (рисунок 59), производим
пересчёт прогибов с учётом таблицы 21.
Для
варианта рамы с круглым сечением на
участке АВ (рисунок 59), производим
пересчёт прогибов с учётом таблицы 21.
Р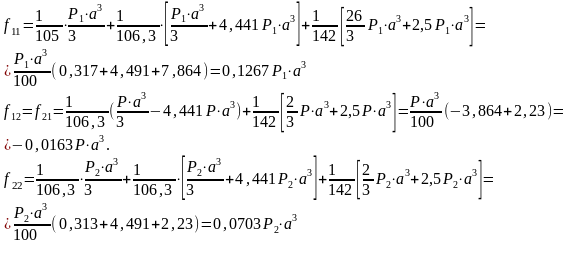
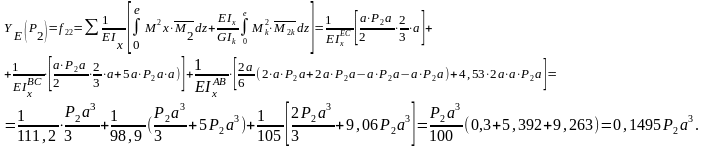
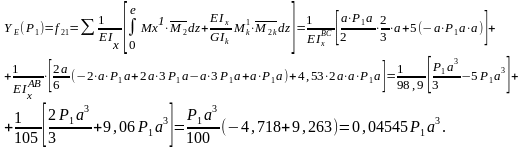 езультаты
расчёта теоретических прогибов сводим
в таблице 22.
езультаты
расчёта теоретических прогибов сводим
в таблице 22.
С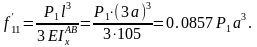 равним
прогиб f11
в плоской
раме с прогибом в консольной балке такой
же длины l
= 3a.
равним
прогиб f11
в плоской
раме с прогибом в консольной балке такой
же длины l
= 3a.
Р1а







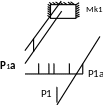
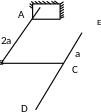

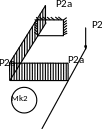
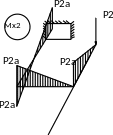
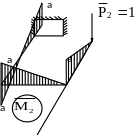
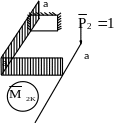
a
B






Рисунок 47 - Эпюры изгибающих и крутящих моментов в раме
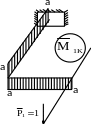
Таблица 21 - Теоретические прогибы двух точек плоской рамы при изгибе с кручением (а=0.3м, P=2 кг)
Прогиб |
Рама рисунок 46а |
Рама рисунок 46б |
Консольная балка |
|||
Формула |
Значение, мм |
Формула |
Значение, мм |
Формула |
Значение, мм |
|
f11 f12 = f21 f22 |
0.22560P1а3 0.04545Pа3 0.14950P2а3 |
12.18 2.45 8.07 |
0.1267 P1а3 -0.0163 Pа3 0.0703 P2а3 |
6.84 -0.88 3.80 |
0.0857P1а3 |
4.62 |
Расчёт на прочность плоской рамы.
Опасное сечение рамы устанавливаем из совместного рассмотрения эпюр изгибающих и крутящих моментов (рисунок 47), оно находится в заделке (сечение А) и соответствует схеме нагружения на свободном конце силой P1, MXA = 3P1а, MKA = P1а. Эпюры нормальных σz и касательных τк напряжений в заделке для прямоугольного и круглого сечений представлены на рисунке 45 от нагрузки P1 = 2кг для размера а = 0.3м.
MXA = 3P1а = 3·2кг·0.3м = 1.8кг∙м,
MKA = P1а = 2кг·0.3м = 0.6кг∙м
Геометрические характеристики сечений двух типов для расчёта напряжений на участке AB даны в таблице 20. Для прямоугольного сечения (рисунок 46) напряжения будут равны.
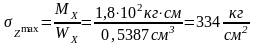
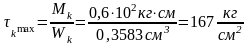
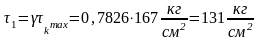
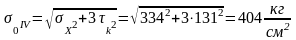
где
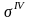 -
приведенное эквивалентное напряжение
по IV
энергетической теории прочности Ван
Мизеса.
-
приведенное эквивалентное напряжение
по IV
энергетической теории прочности Ван
Мизеса.
Для круглого сечения (рисунок 45) напряжения будут равны
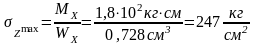
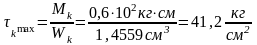
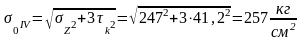
Таким
образом, при значении допускаемого
напряжения
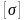 для стали ст. 45 максимальная величина
силы P1
не должна превышать для рамы прямоугольного
сечения
для стали ст. 45 максимальная величина
силы P1
не должна превышать для рамы прямоугольного
сечения
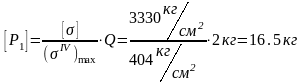
Число ступеней загружения грузами весом 2кг не должно превышать восьми
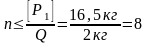
С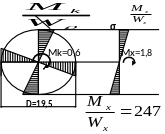
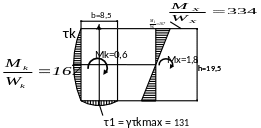 равним
максимальные эквивалентные напряжения
в раме прямоугольного и круглого сечения
такой же длины от нагрузки Р=2 кг (рисунок
46).
равним
максимальные эквивалентные напряжения
в раме прямоугольного и круглого сечения
такой же длины от нагрузки Р=2 кг (рисунок
46).
Рисунок 48 - Эпюры нормальных σz [кг/см2] и касательных τк напряжений
в прямоугольном и в круглом сечении бруса (MX = 1.8кгּм, MK = 0.6 кгּм)
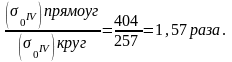
Порядок проведения испытаний.
Нагрузка прикладывается ступенями грузами Q=2кг (не более 8-ми ступеней) по двум схемам:
1) в сечении D сила P1;
2) в сечении E прикладывается сила P2 .
На каждой ступени измеряются прогибы в точках D и E по разности отчётов мерительного угольника А1 для точки D и А2 для точки Е (рисунок 46).
Показания заносятся в таблицу результатов испытаний (табл. 22, 23)
Таблица 22 – Результаты испытания плоской рамы (рисунок 47-а)
на изгиб с кручением от загружения силой Р1
№ ступени |
Нагрузка P1, кг |
Отчёты мерительного угольника А1, А2 и прогибы f, мм |
||||||
А1 (для точки D) |
f11 |
Δf11 |
А2 (для точки Е) |
f21 |
Δf21 |
|||
1 2 3 4 5 |
0 2 4 6 8 10 |
180 169 157 145 134 122 |
0 11 23 35 46 58 |
− 11 12 12 11 12 |
188 185 182 179 176 173 |
0 3 6 9 12 15 |
− 3 3 3 3 3 |
|
|
Δ P1 =2кг |
Δf11ср=11,6 δf11
|
Δf21ср=3
|
|||||
Таблица 22 а – Результаты испытания плоской рамы (рисунок 47-а)
на изгиб с кручением от загружения силой Р2
№ ступени |
Нагрузка P2, кг |
Отчёты мерительного угольника А1, А2 и прогибы f, мм |
||||||
А1 (для точки D) |
f 12 |
Δf12 |
А2 (для точки Е) |
f22 |
Δf22 |
|||
1 2 3 4 5 |
0 2 4 6 8 10 |
180 176 174 171 168 165 |
0 4 6 9 12 15 |
− 4 2 3 3 3 |
188 180 173 165 158 150 |
0 8 15 23 30 38 |
− 8 7 8 7 8 |
|
|
Δ P2 = 2кг |
Δf12ср=3
|
Δf22ср=7,6 δf22 |
|||||
Таблица 23 – Результаты испытания плоской рамы (рисунок 47-б)
на изгиб с кручением от загружения силой Р1
№ ступени |
Нагрузка P1, кг |
Отчёты мерительного угольника А1, А2 и прогибы f, мм |
|||||
А1 (для точки D) |
f11 |
Δf11 |
А2 (для точки Е) |
f21 |
Δf21 |
||
1 2 3 4 5 |
0 2 4 6 8 10 |
177 170 164 157 150 144 |
0 7 13 20 27 33 |
− 1 8 8 7 7 |
188 189 189 189 189 190 |
0 -1 -1 -1 -1 -2 |
− -1 0 0 0 -1 |
|
Δ P1 = 2кг |
Δf11ср=6,6 δf11
|
Δf21ср=-0,4
|
||||
Таблица 23 а – Результаты испытания плоской рамы (рисунок 47-б)
на изгиб с кручением от загружения силой Р2
№ ступени |
Нагрузка P1, кг |
Отчёты мерительного угольника А1, А2 и прогибы f, мм |
|||||
А1 (для точки D) |
f12 |
Δf12 |
А2 (для точки Е) |
f22 |
Δf22 |
||
1 2 3 4 5 |
0 2 4 6 8 10 |
178 178 179 179 178 179 |
0 0 1 0 0 1 |
− 0 1 -1 0 1 |
190 187 183 180 176 172 |
0 3 7 10 14 18 |
− 3 4 3 4 4 |
|
Δ P2 = 2кг |
Δf12ср=0,2
|
Δf22ср=3,6 δf22
|
||||
ВЫВОДЫ
1) Экспериментально подтверждается справедливость универсальной формулы упругих перемещений бруса - интеграла Мора- Максвелла - при изгибе с кручением. Максимальная погрешность упругого прогиба для рамы прямоугольного сечения (рисунок 47 а) составляет 5,82%, для рамы круглого сечения (рисунок 47 б) погрешность составляет 5,3%.
2) Основной вклад в максимальный прогиб рамы дают деформации кручения, прогиб в раме превышает прогиб в консольной балке такой же длины в 2,6 раза.
3) Прочность плоской рамы круглого сечения выше, чем прямоугольного сечения (при высоте, равной диаметру) в 1,57 раза.

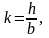
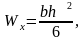 см3
см3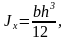 см4
см4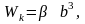 см3
см3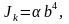 см4
см4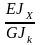
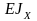 кг·м2
кг·м2