Пирамида
Математика, Алгебра, Геометрия
В некоторой плоскости построим многоугольник (n-угольник)
AI,AZ,—1",
а вне берем точку Р. Эту точку соединим отрезками прямых со всеми вершинами многоугольника. Получим n треугольников
(на рис. 54 изображен случай n = 5).
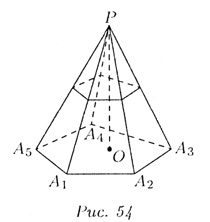
Геометрическая фигура, состоящая из n треугольников и первоначальпого n-угольника, называется пирамидой. Обозначение: PA1A2....An, P — вершина пирамиды. Часть пространства, расположенного внутри пирамиды, также присоединяется к пирамиде. Многоугольник A1A2....Anназывается основанием, треугольники — боковыми гранями, их стороны — ребрами. Отрезки PA1 , PA2....PAn называются боковыми ребрами, стороны многоугольника — ребрами (сторонами) основания. Отрезок ОР перпендикуляра, опушенного из вершины Р на плоскость основания пирамиды, называется ее высотой.
В виде пирамиды строят купола отдельных зданий.
Треугольная пирамида называется тетраэдром. Плоскость, параллельная основанию пирамиды и пересекающая ее, отсекает подобную пирамиду, а в сечении получается многоугольник, подобный основанию. Оставшаяся часть называется усеченной пирамиды.
Объем призмы
Математика, Алгебра, Геометрия
Объем призмы ранен V = Sоснов • H. где Sоснов — площадь основания призмы. H — ее высота.
Исходим из известного факта: объем параллелепипеда, равен
Vпар = Sоснов • H
(Sоснов - площадь основания, H — высота).
Начнем с частного случая. Пусть нам дана треугольная призма.
Достроим ее до параллелепипеда. Следовательно, параллелепипед состоит из двух равных призм, поэтому
С другой стороны,
а высота призмы и параллелепипеда общая. Из равенства
следует, что
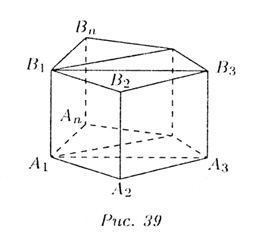
Переходим теперь к общему случаю. Дана произвольная призма. В ее основании лежит многоугольник. Проведя в нем диагонали, исходящие, из одной вершины, разбиваем многоугольник на треугольники (рис. 39). Сечения, проведенные через эти диагонали и соответствующие боковые ребра призмы делят ее на определенное число n треугольных призм. Для призмы с номером k объем равен
Vk = Sk • H
где Sk — площадь ее основания, H — высота первоначальной призмы. Складывая объем треугольных призм, получаем объем первоначальной призмы:
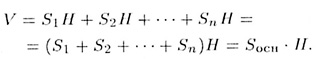
Формула установлена.
Логарифмическая функция, ее свойства и график
Математика, Алгебра, Геометрия
Логарифмическая функция у = loga x (а > 0, a # 1 ) определена только при х > 0 (у = loga x <=> х = аy) и обладает следующими свойствами:
1. монотонности: 0 < x1 < x2<=>
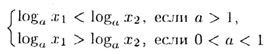
2. сохранения знака:у = loga x > 0 <=>
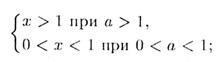
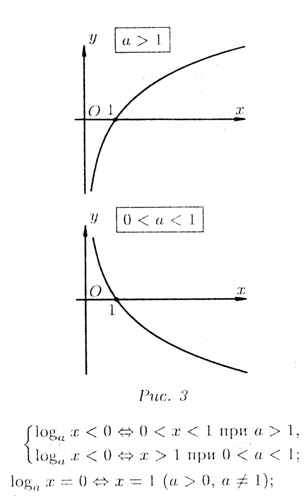
3. асимптотического стремления к бесконечности: при х —> 0 (x > 0),
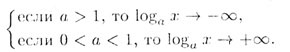
Прямая х = 0 называется вертикальной асимптотой графика функции у = loga x.