Признак перпендикулярности плоскостей
Математика, Алгебра, Геометрия
Две пересекающиеся плоскости образуют четыре двугранных угла с общим ребром: пары вертикальных углов равны, а сумма двух смежных углов равна 180°. Если один из четырех углов прямой, то три остальных также равны и прямые. Две плоскости называются перпендикулярными, если угол между ними прямой.
Теорема. Если плоскость проходит через прямую, перпендикулярную к другой плоскости, то эти плоскости перпендикулярны.
Пусть и - две плоскости такие, что проходит через прямую АВ, перпендикулярную к и пересекающуюся с ней в точке А (рис. 49). Докажем, что _|_ . Плоскости и пересекаются по некоторой прямой AC, причем AВ _|_ AC, т.к. AB _|_ . Проведем в плоскости прямую AD, перпендикулярную прямой АС.
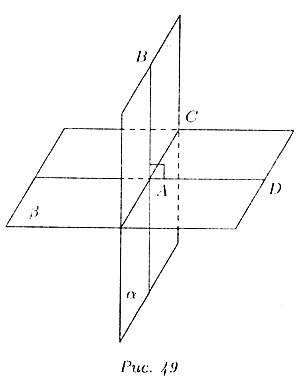
Тогда угол BAD — линейный угол двугранного угла, образованного и . Но < ВАD - 90° (ибо AB _|_ ), а тогда, по определению, _|_ . Теорема доказана.
Сфера и шар (формулировки и примеры)
Математика, Алгебра, Геометрия
Сферой называется поверхность, состоящая из всех точек пространства, расположенных на данном расстоянии R от данной точки О.
Данная точка называется центром сферы, а данное расстояние - радиусом сферы.
Отрезок, соединяющий центр О сферы с любой ее точки М, также называется радиусом.
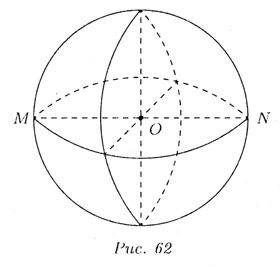
Отрезок, соединяющий две точки сферы и проходящий через ее центр, называется ее диаметром, а соответствующие концы диаметра называются диаметрально противоположными. Диаметр D сферы равен двум радиусам: D = 2R (см. рис. 62).
Тело, ограниченное сферой, называется шаром. Центр, радиус, диаметр сферы являются также центром, радиусом, диаметром шара. Шар радиуса R с центром в точке О содержит все точки пространства, которые расположены от точки О на расстоянии не больше, чем R. Сечения сферы (шара) плоскостью являются окружностями (кругами).
Перпендикулярность прямой и плоскости
Математика, Алгебра, Геометрия
Прямая а, пересекающая плоскость , называется перпендикулярной этой плоскости, если она перпендикулярна любой прямой плоскости, проходящей через точку О пересечения прямой a и плоскости .
Теорема. Если прямая а перпендикулярна двум прямым b и с, плоскости , проходящим через точку О пересечения а и , то а перпендикулярна .
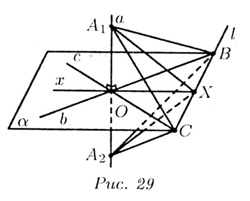
Пусть дана прямая a и две прямые b и с, лежащие в плоскости : а _|_ b, a _|_ с (рис. 29), О — точка пересечения b и с. Пусть х — другая (отличная от b и с) прямая, лежащая в и проходящая через точку О. Надо доказать, что a _|_ x.
Проводом
в плоскости
произвольную
прямую l, пересекающую прямые b и с и не
проходящую через точку О. Обозначим В
= l
b,
С = l
с
и X = l
х.
Берем на а две точки А1 и
А2,
так что OА1 =
ОА2 (А1 и
А2 —
по разные стороны от
.
Рассмотрим образовавшиеся треугольники.
1. 
А1ОВ
=
А2ОВ
как прямоугольные треугольники с ранными
катетами. Значит, А1В
= А2В.
2. А1ОС = А2ОС по аналогичной причине. Отсюда А1С = А2С.
3. А1СВ = А2СВ по трем сторонам. Значит, < А1BC = < А2BC .
4. Обратимся к треугольникам А1BX и А2BX. В них А1B = А2B, ВХ — общая, < А1BX = < А2BX (по первому признаку). Отсюда следует, что А1X = А2X. Значит, А1XА2 - равнобедренный, О — середина А1А2. Значит, ОX - медиана, а тогда и высота, равнобедренного треугольника. Следовательно, a _|_ х.
Теорема. Если прямая, проведенная на плоскости через основание наклонной, перпендикулярна ее проекции, то она перпендикулярна и самой наклонной. И обратно, если прямая на плоскости перпендикулярна наклонной, то она перпендикулярна и проекции наклонной.
Дана наклонная МО с проекцией NO и MN _|_ , в частности, MN _|_ NO (рис. 63).
Дано: PQ _|_ NO (т.е. PQ _|_ а1).
Надо доказать, что PQ _|_ МО (PQ _|_ а).
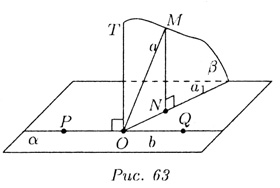
а) Через точку О проводим прямую ОТ, перпендикулярную плоскости . Тогда ОТ || MN, т.к. и MN _|_ и ОТ _|_ . Прямые ОТ и ON образуют плоскость , и PQ перпендикулярна этой плоскости, ибо PQ _|_ ON и PQ _|_ ОТ. Значит, PQ _|_ ОМ, т. е. b _|_ а, т.к. ОM — прямая из плоскости .
Аналогично доказывается и обратная теорема. Если b _|_ а и b _|_ ОТ, то b _|_ (проходящей через ОТ и ОМ), а значит, и проекции а1, принадлежащей этой плоскости . Теорема доказана.