
Шпоры к междису / ДМ
.doc« Дискретная
математика»
Дискретная
математика»
1) СДНФ (0,0,0,0,0,0,1,1)
|
№ |
X1 |
x2 |
x3 |
f |
|
0 |
0 |
0 |
0 |
0 |
|
1 |
0 |
0 |
1 |
0 |
|
2 |
0 |
1 |
0 |
0 |
|
3 |
0 |
1 |
1 |
0 |
|
4 |
1 |
0 |
0 |
0 |
|
5 |
1 |
0 |
1 |
0 |
|
6 |
1 |
1 |
0 |
1 |
|
7 |
1 |
1 |
1 |
1 |
берём строки где f=1
6:
![]()
7:
![]()
![]()
2 )СДНФ (0,0,0,1,0,0,1,0)
|
№ |
X1 |
x2 |
x3 |
f |
|
3 |
0 |
1 |
1 |
1 |
|
6 |
1 |
1 |
0 |
1 |
берём строки где f=1
6:
![]()
3:
![]()
![]()
3) СДНФ (0,1,0,0,0,1,0,0)
|
№ |
X1 |
x2 |
x3 |
f |
|
1 |
0 |
0 |
1 |
1 |
|
5 |
1 |
0 |
1 |
1 |
берём строки где f=1
1:
![]()
5:
![]()
![]()
4) СДНФ (1,0,0,0,0,0,1,0)
|
№ |
X1 |
x2 |
x3 |
f |
|
0 |
0 |
0 |
0 |
1 |
|
6 |
1 |
1 |
0 |
1 |
берём строки где f=1
0:
![]()
6:
![]()
![]()
5) СДНФ (0,0,0,0,0,1,0,1)
|
№ |
X1 |
x2 |
x3 |
f |
|
5 |
1 |
0 |
1 |
1 |
|
7 |
1 |
1 |
1 |
1 |
берём строки где f=1
5:
![]()
7:
![]()
![]()
6 )
СКНФ
(1,1,0,1,1,1,1,1)
)
СКНФ
(1,1,0,1,1,1,1,1)
|
№ |
X1 |
x2 |
x3 |
f |
|
0 |
0 |
0 |
0 |
1 |
|
1 |
0 |
0 |
1 |
1 |
|
2 |
0 |
1 |
0 |
0 |
|
3 |
0 |
1 |
1 |
1 |
|
4 |
1 |
0 |
0 |
1 |
|
5 |
1 |
0 |
1 |
1 |
|
6 |
1 |
1 |
0 |
1 |
|
7 |
1 |
1 |
1 |
1 |
берём строки где f=0
2:
![]()
![]()
7) СКНФ (1,1,1,1,0,1,1,1)
|
№ |
X1 |
x2 |
x3 |
f |
|
4 |
1 |
0 |
0 |
0 |
берём строки где f=0
4:
![]()
![]()
8) СКНФ (1,1,1,1,1,0,1,1)
|
№ |
X1 |
x2 |
x3 |
f |
|
5 |
1 |
0 |
1 |
0 |
берём строки где f=0
5:
![]()
![]()
9) СКНФ (1,0,1,1,1,1,1,1)
|
№ |
X1 |
x2 |
x3 |
f |
|
1 |
0 |
0 |
1 |
0 |
берём строки где f=0
1:
![]()
![]()
10) СКНФ (1,1,1,0,1,1,1,1)
|
№ |
X1 |
x2 |
x3 |
f |
|
3 |
0 |
1 |
1 |
0 |
берём строки где f=0
3:
![]()
![]()
11) Полином Жегалкина (0,1,1,0)
Общий вид полинома:
![]() f(0,0)=a0=0
f(0,0)=a0=0
f(0,1)=a2a0=a2 0=1 => a2=1
f(1,0)=a1a0=a1 0=1 => a1=1
f(1,1)=a12a1a2a0=
=a12110= a120=0
=> a12=0
f=X1X2
1
 2)
полином
Жегалкина (0,1,0,1)
2)
полином
Жегалкина (0,1,0,1)
Общий вид полинома:
![]() f(0,0)=a0=0
f(0,0)=a0=0
f(0,1)=a2a0=a2 0=1 => a2=1
f(1,0)=a1a0=a1 0=0 => a1=0
f(1,1)=a12a1a2a0=
=a12100= a121=1
=> a12=0
f= X2
13) полином Жегалкина (1,0,1,0)
Общий вид полинома:
![]() f(0,0)=a0=1
f(0,0)=a0=1
f(0,1)=a2a0=a2 1=0 => a2=1
f(1,0)=a1a0=a1 1=1 => a1=0
f(1,1)=a12a1a2a0=
=a12101= a120=0
=> a12=0
f= X21
14) полинома Жегалкина (1,1,1,0)
Общий вид полинома:
![]()
f(0,0)=a0=1
f(0,1)=a2a0=a2 1=1 => a2=0
f(1,0)=a1a0=a1 1=1 => a1=0
f(1,1)=a12a1a2a0=
=a12001= a121=0
=> a12=1
f= X1X21
15) полинома Жегалкина (1,0,0,1)
Общий вид полинома:
![]()
f(0,0)=a0=1
f(0,1)=a2a0=a2 1=0 => a2=1
f(1,0)=a1a0=a1 1=0 => a1=1
f(1,1)=a12a1a2a0=
=a12111= a121=1
=> a12=0
f= X1X21
16)
Упростить выражение
![]()
17)
Упростить выражение
![]()
18)
Упростить выражение
![]()
19)
Упростить выражение
![]()
20)
Упростить выражение
![]() 21)
Упростить выражение
21)
Упростить выражение
![]() 22)
Упростить
выражение
22)
Упростить
выражение
![]() 23)
Упростить выражение
23)
Упростить выражение
![]()
2 4)
Упростить
выражение
4)
Упростить
выражение
![]()
25)
Упростить
выражение
![]()
26)
Упростить
выражение
![]()
27)
Упростить
выражение
![]()
28)Упростить
выражение
![]() 29)
Упростить
выражение
29)
Упростить
выражение
![]()
30)
Упростить
выражение
![]()
31)являются отношениями эквивалентности.
Ответ:2, потому что явл-ся рефлексивным, симметричн. и транзитивн.
1) “<” на множестве действительных чисел;
2) “быть подобными геометрическими фигурами”;
3) “” на множестве целых чисел;
32)являются отношениями частичного порядка
Ответ:1, потому что явл-ся рефлексивным, антисимметричн. и транзитивн.
1) “” на множестве всех множеств;
2) “быть подобными геометрическими фигурами”;
3) “” на множестве целых чисел;
33)являются отношениями линейного порядка.
Ответ:1
1) “” на множестве действительных чисел;
2) “быть подобными геометрическими фигурами”;
3) “” на множестве всех множеств
34) Какие из следующих отношений не являются отношениями эквивалентности
Ответ:3
1) “=” на множестве действительных чисел;
2) “быть подобными геометрическими фигурами”;
3) “иметь непустое пересечение” на множестве непустых множеств
35)являются функционально полными
Ответ:1,2
-
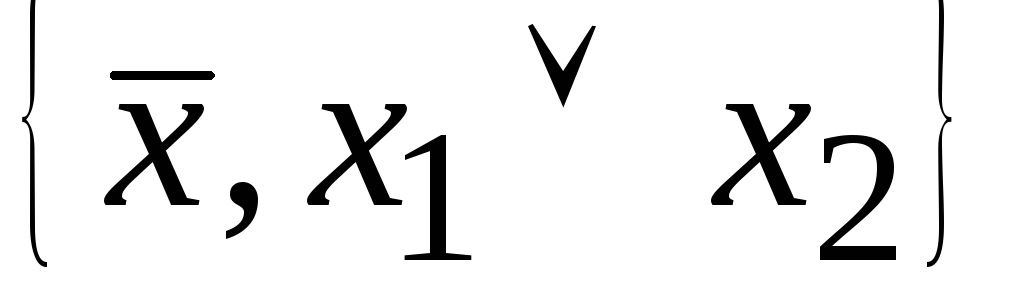 -
да
-
да -
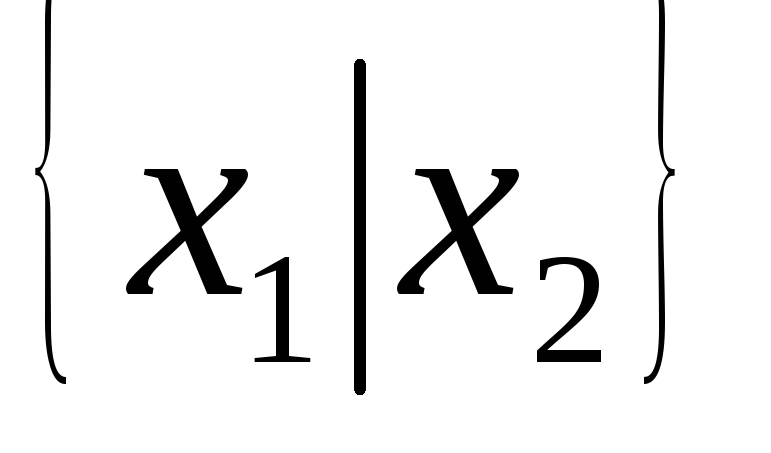 -
да
-
да -
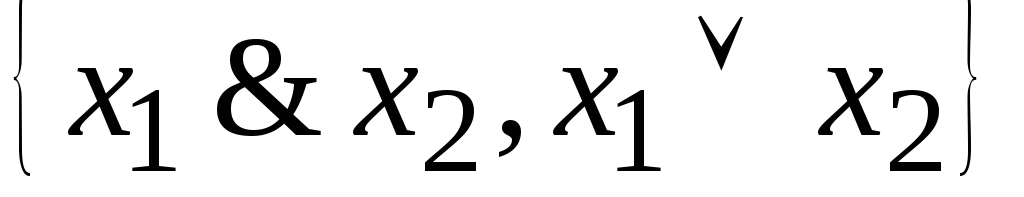 -нет
-нет
т.к через них можно выразить все функции стандартного базиса
1)![]()
2)![]()
![]()
