3.1.2 Дисконтирование по простым процентам

Прорабатывая материал предыдущих глав вы уже убедились, что важнейшей характеристикой любой финансовой операции является современная стоимость (величина) потоков платежей PV, определяемая методом дисконтирования.

В зависимости от вида процентной ставки, при анализе краткосрочных финансовых операций применяют два метода дисконтирования – математическое и коммерческое (т.н. банковский учет).

В первом случае в качестве нормы приведения используют ставку r, применяемую при наращении (3.1). Во втором случае в роли нормы приведения выступает т.н. учетная ставка, для обозначения которой в дальнейшем будет использоваться символ d.

Математическое дисконтирование

Математическое дисконтирование представляет собой задачу обратную наращению и сводится к определению величины PV по известным значениям величин FV, r, n. С учетом принятых обозначений формула дисконтирования по ставке r будет иметь следующий вид:

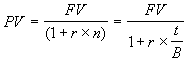. (3.4)

Разность FV - PV называют дисконтом или скидкой, а используемую норму приведения r – декурсивной ставкой процентов.

Банковский или коммерческий учет

Этот метод дисконтирования применяется, в основном, при банковском учете векселей, смысл которого будет рассмотрен ниже. Суть данного метода заключается в том, что проценты начисляются на сумму, подлежащую уплате в конце срока операции. При этом применяется учетная ставка d. Формула дисконтирования по учетной ставке имеет следующий вид:

. (3.5)

При дисконтировании по учетной ставке чаще всего используют временную базу 360/360 или 360/365. Используемую при этом норму приведения d называют антисипативной ставкой процентов.

Нетрудно заметить, что применение двух рассмотренных методов дисконтирования приводит к разным результатам, даже при r = d. Учетная ставка d дает более быстрый рост задолженности, чем обычная ставка r.

Учетная ставка d иногда применяется и для наращения по простым процентам. Необходимость в таком наращении возникает при определении будущей суммы контракта, например – общей суммы векселя. Формула определения будущей величины в этом случае имеет следующий вид:

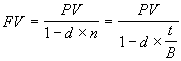. (3.6)

3.1.3 Определение процентной ставки и срока проведения операции

Величина процентной ставки r или учетной ставки d может быть определена из соотношений (3.1) и (3.5). Решив соответствующие уравнения относительно r или d получим:

. (3.7)

. (3.8)

Соответственно срок операции в днях определяется как:

. (3.9)

. (3.10)

3.1.4 Эквивалентность процентных ставок r и d

Принцип эквивалентности процентных ставок широко применяется в финансовом анализе. Его используют при сравнении условий сделок, замене одного вида ставок на другой, определении эффективности операций и т.д.

В общем случае две различные процентные ставки считаются эквивалентными, если их использование при одинаковых условиях сделки приводит к одному и тому же финансовому результату.

В настоящей работе мы ограничимся рассмотрением условий эквивалентности ставки наращения r и учетной ставки d, исчисляемых по методу простых процентов.

Вывод формул эквивалентности базируется на равенстве соответствующих множителей наращения:

1 + nr = (1 - nd)^-1 . (3.11)

С учетом n = t / B, для операций с продолжительностью менее года соотношения эквивалентности примут следующий вид:

а) временная база ставок одинакова и равна В (360 или 365 дней)

. (3.12)

. (3.13)

б) временная база ставки r равна 365 дням, а d – 360 дням

. (3.14)

. (3.15)

Детальное изложение методов процентных вычислений и их применения в финансовом анализе можно найти в [7, 13].

В дальнейшем, рассматривая методы анализа краткосрочных ценных бумаг, мы будем использовать ставку наращения r и математическое дисконтирование. Техника применения учетной ставки d и соответствующего ей метода дисконтирования будет показана при рассмотрении анализа операций с векселями