
- •1.Кинематика точки. Система координат. Траектория движения точки. Способы задания уравнений движения тела.
- •5.Относительное движение. Абсолютная скорость и абсолютное ускорение.
- •10. Центр тяжести. Методы нахождения центров тяжести (симметричные тела, отрицательные объемы). Центры тяжести простейших фигур.
- •11.Введение в динамику. Второй закон ньютона.
- •12.Дифференциальные движения материальной точки (естественный и координатный способ).
- •13.Прямолинейное движение материальной точки.
- •14.Свободные колебания материальной точки.
- •15.Свободные колебания с учетом сопротивления.
- •18.Теорема об изменении количества движения материальной системы.
- •19.Теорема Эйлера.
- •20.Теорема о движении центра масс.
- •21.Теорема об изменении момента количества движения материальной системы.
- •22.Динамика вращательного движения вокруг неподвижной оси.
- •23.Работа и мощность.
- •24.Теорема об изменении кинетической энергии. Теорема Кенига.
- •25.Принцип Даламбера.
- •26.Принцип Лагранжа (принцип возможных перемещений).
- •28.Уравнение Лагранжа 2-го рода.
18.Теорема об изменении количества движения материальной системы.
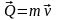 – количество
движения материальной точки,
– количество
движения материальной точки,
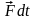 – элементарный импульс силы.
– элементарный импульс силы.
 – элементарное изменение количества
движения материальной точки равно
элементарному импульсу силы, приложенной
к этой точке (теорема в дифференц-ной
форме) или
– элементарное изменение количества
движения материальной точки равно
элементарному импульсу силы, приложенной
к этой точке (теорема в дифференц-ной
форме) или
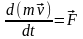 –
производная по времени от количества
движения материальной точки равна
равнодействующей сил, приложенных к
этой точке. Проинтегрируем:
–
производная по времени от количества
движения материальной точки равна
равнодействующей сил, приложенных к
этой точке. Проинтегрируем:
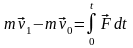 – изменение количества движения
материальной точки за конечный промежуток
времени равно элементарному импульсу
силы, приложенной к этой точке, за тот
же промежуток времени.
– изменение количества движения
материальной точки за конечный промежуток
времени равно элементарному импульсу
силы, приложенной к этой точке, за тот
же промежуток времени.
 –
импульс силы за промежуток времени
[0,t].
В проекциях на оси координат:
–
импульс силы за промежуток времени
[0,t].
В проекциях на оси координат:
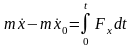 и т.д.
и т.д.
19.Теорема Эйлера.
Найдём
число координат, определяющих положение
абсолютно твёрдого тела. Определить
положение тела => определить координаты
![]() точки
относительно некоторой системы отсчёта
в
момент
времени. П
точки
относительно некоторой системы отсчёта
в
момент
времени. П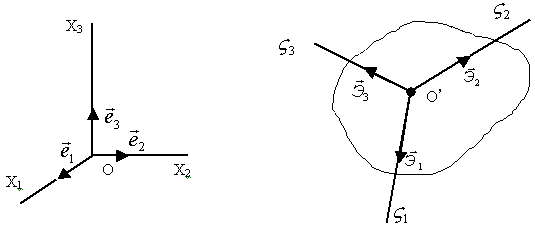 усть
Х1 , Х2 , Х3 – неподвижные оси (рис. 38);
орты:
усть
Х1 , Х2 , Х3 – неподвижные оси (рис. 38);
орты:
![]() [декартова система].
[декартова система].
,
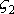 ,
,
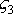 , - оси, жёстко связанные с телом; орты:
, - оси, жёстко связанные с телом; орты:
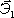 ,
,
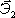 ,
,
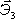 - [декартова система]. Так как координаты
точек относительно собственных осей
- [декартова система]. Так как координаты
точек относительно собственных осей
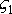 ,
,
не зависят от времени, то задача сводится
к определению положения координатных
осей, жёстко связанных с телом
(подвижных), относительно неподвижных
осей Х1 , Х2 , Х3. Составим таблицу косинусов
углов между осями Х и
,
,
не зависят от времени, то задача сводится
к определению положения координатных
осей, жёстко связанных с телом
(подвижных), относительно неподвижных
осей Х1 , Х2 , Х3. Составим таблицу косинусов
углов между осями Х и
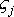 :
:
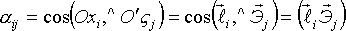
![]() -
скалярное произведение. Так как системы
координат ортогональны, то скалярное
произведение:
-
скалярное произведение. Так как системы
координат ортогональны, то скалярное
произведение:
![]() , где
, где
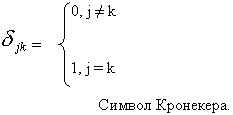
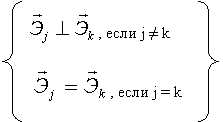
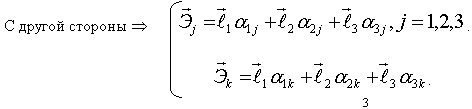
![]() Итак:
Итак:
![]() .
Число таких соотношений = 6 (Из 9 – ти в
силу симметрии по jи k). Имеем 6 соотношений
для 9 косинусов => 3 косинуса
.
Число таких соотношений = 6 (Из 9 – ти в
силу симметрии по jи k). Имеем 6 соотношений
для 9 косинусов => 3 косинуса
![]() , не расположенные в одном столбце, или
в одной строке, могут быть приняты за
независимые, а остальные можем определить
из составленных 6 – ти
, не расположенные в одном столбце, или
в одной строке, могут быть приняты за
независимые, а остальные можем определить
из составленных 6 – ти
 соотношений.
соотношений.
Кроме того => три координаты определяют положение точки О’ – начало системы , , .
Но
9 координат и 3 соотношение длин:
![]() .
это условия постоянства расстояний
между точками в абсолютно твёрдом
теле.Выведем формулу Эйлера для
распределения скоростей точек абсолютно
твёрдого тела.
.
это условия постоянства расстояний
между точками в абсолютно твёрдом
теле.Выведем формулу Эйлера для
распределения скоростей точек абсолютно
твёрдого тела.
![]() , 1)
, 1)
![]() ,
,
![]() -
скорость точки О’,
-
скорость точки О’,![]() - скорость точки Q во вращательном
движении тела (так как длина постоянна).
Так как координаты
- скорость точки Q во вращательном
движении тела (так как длина постоянна).
Так как координаты
![]() точки Qпостоянны, то
точки Qпостоянны, то
![]() .
Тогда: 2)
.
Тогда: 2)
![]() ,
,
где
![]() . Скорость точки Q:
. Скорость точки Q:
![]() .
3) Выразим
.
3) Выразим
![]() и производные через направляющие
косинусы
и производные через направляющие
косинусы
![]() :
:
![]() .
Тогда:
.
Тогда:
![]() (в неподвижной системе). 4) Проекция
(в неподвижной системе). 4) Проекция
![]() на ось
на ось
![]() (k= 1,2,3):
(k= 1,2,3):
![]() .
Скорости точек во вращательном движении
– линейные функции координат точек.
5) Получим более простую и наглядную
форму закона распределения скоростей,
используя свойства функции
.
Скорости точек во вращательном движении
– линейные функции координат точек.
5) Получим более простую и наглядную
форму закона распределения скоростей,
используя свойства функции
![]() .
.
![]() ,
Дифференцируем по t:
,
Дифференцируем по t:
![]() .
По свойству производной от произведения:
при j= k => ,
.
По свойству производной от произведения:
при j= k => ,
![]() при j≠ k=> .
при j≠ k=> . ![]() Свойства:а)
симметрия по kи j; б) при j= k=>равенство
«0»; в) размерность t-1 , т. е. угловая
скорость (угол в радианах), так как
Свойства:а)
симметрия по kи j; б) при j= k=>равенство
«0»; в) размерность t-1 , т. е. угловая
скорость (угол в радианах), так как
![]() -
скорость.
-
скорость.
П окажем,
что
окажем,
что

Действительно:
![]() ,
,
![]() - по аналогии. Итак:
- по аналогии. Итак:
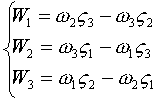 или: 7)
или: 7)
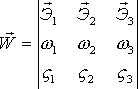 ,
где
,
где
![]() - единичные вектора, жёстко связанные
с телом. Положим
- единичные вектора, жёстко связанные
с телом. Положим
![]() - вектор, где
- вектор, где
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,8)
Тогда:
,8)
Тогда:
![]()
![]() -Описывает распределение скоростей.
Назовём
вектором мгновенной угловой скорости,
а прямая на которой он располагается,
в рассматриваемый момент времени,
проходящую через точку О’ – осью
мгновенного вращения, или мгновенной
осью. Таким образом, закон распределения
скоростей точек абсолютно твёрдого
тела в любом движении:
-Описывает распределение скоростей.
Назовём
вектором мгновенной угловой скорости,
а прямая на которой он располагается,
в рассматриваемый момент времени,
проходящую через точку О’ – осью
мгновенного вращения, или мгновенной
осью. Таким образом, закон распределения
скоростей точек абсолютно твёрдого
тела в любом движении:
![]() .
.
