
- •Математические модели и их виды. Классификация моделей
- •Экстемум функций многих переменных. Линии уровня. Градиент. Условный экстремум
- •Постановка и свойства задачи линейного программирования. Геометрическая интерпретация.
- •Симплекс- метод решения задачи линейного программирования
- •Двойственная задача линейного программирования, ее интерпретация и свойства
- •Транспортная задача и ее математическая модель. Определение опорного плана транспортной задачи
- •Определение оптимального плана транспортной задачи методом потенциалов. Приемы решения методом потенциалов транспортных задач
- •Геометрическая и экономическая интерпретация задач нелинейного программирования. Метод множителей Лагранжа. Возможности численного решения нелинейных и целочисленных задач
- •Основные понятия и общая характеристика задач динамического программирования, их геометрическая и экономическая интерпретация. Нахождение решение задач методом динамического программирования
- •Оптимизационные задачи, решаемые при помощи графов. Алгоритмы на графах
- •Нахождение максимального и минимального пути в графе. Решение транспортной задачи с помощью графов
- •Основные понятия теории массового обслуживания. Компоненты и классификация моделей систем массового обслуживания
- •Определение характеристик систем массового обслуживания. Марковский процесс. Уравнения Колмогорова
- •Одноканальные и многоканальные смо с пуассоновским входным потоком и экпотенциальным распределением длительности обслуживания
- •Основные количественные характеристики простейшего потока.
- •Распределение интервала времени t между произвольными двумя соседними событиями простейшего потока.
- •Одноканальная смо с отказами и ее характеристики
- •Многоканальная смо с отказами и ее характеристики
- •Одноканальная смо с ожиданием и его характеристики. Формула Литтла
- •Многоканальное смо с ожиданием и ее характеристики. Формула Литтла
- •Простейшие задачи решаемые методом имитационного моделирования. Теоретические основы метода имитационного моделирования
- •Моделирование смо с использованием метода Монте- Карло
- •Имитация процессов, происходящих во времени. Основная идея и методы прогнозирования. Количественные методы прогноза. Прогнозирование временных рядов. Модель линейной регрессии
- •Предмет теории игр, основные понятия. Матричные игры. Цны, доминирующие и оптимальные стратегии игр. Принцип минмакса. Решение задач теории игр в чистых стратегиях
- •Стратегические игры в смешанных стратегиях. Основная теорема теории игр. Решение задачи в смешанных стратегиях методами линейного программирования
- •Оценка сложных систем в условиях неопределенности. Матрица рисков. Критерии: Байеса, Лапласа, Вальда, Сэвиджа, Гурвица.
Двойственная задача линейного программирования, ее интерпретация и свойства
Понятие двойственности
рассмотрим на примере задачи оптимального
использования сырья. Пусть на предприятии
решили рационально использовать отходы
основного производства. В плановом
периоде появились отходы сырья m видов
в объемах ![]() единиц
единиц ![]() .
Из этих отходов, учитывая специализацию
предприятия, можно наладить выпуск n
видов неосновной продукции. Обозначим
через
.
Из этих отходов, учитывая специализацию
предприятия, можно наладить выпуск n
видов неосновной продукции. Обозначим
через ![]() норму
расхода сырья i-го вида на единицу
j-й
норму
расхода сырья i-го вида на единицу
j-й ![]() продукции,
продукции, ![]() -
цена реализации единицы j-й продукции
(реализация обеспечена). Неизвестные
величины задачи:
-
цена реализации единицы j-й продукции
(реализация обеспечена). Неизвестные
величины задачи: ![]() — объемы
выпуска j-й
продукции, обеспечивающие предприятию
максимум выручки.
Математическая модель
задачи:
— объемы
выпуска j-й
продукции, обеспечивающие предприятию
максимум выручки.
Математическая модель
задачи:
![]() (2.23)
(2.23)
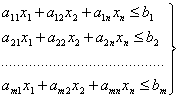 (2.24)
(2.24)
![]()
![]() (2.25)
Предположим далее, что с самого начала
при изучении вопроса об использовании
отходов основного производства на
предприятии появилась возможность
реализации их некоторой организации.
Необходимо установить прикидочные
оценки (цены) на эти отходы. Обозначим
их
(2.25)
Предположим далее, что с самого начала
при изучении вопроса об использовании
отходов основного производства на
предприятии появилась возможность
реализации их некоторой организации.
Необходимо установить прикидочные
оценки (цены) на эти отходы. Обозначим
их ![]() .
Оценки должны быть установлены исходя
из следующих требований, отражающих
несовпадающие интересы предприятия и
организации:
1) общую
стоимость отходов сырья покупающая
организация стремится минимизировать;
2) предприятие согласно уступить отходы
только по таким ценам, при которых оно
получит за них выручку, не меньшую той,
что могло бы получить, организовав
собственное производство.
Эти требования формализуются в виде
следующей ЗЛП.
Требование
1 покупающей организации – минимизация
покупки:
.
Оценки должны быть установлены исходя
из следующих требований, отражающих
несовпадающие интересы предприятия и
организации:
1) общую
стоимость отходов сырья покупающая
организация стремится минимизировать;
2) предприятие согласно уступить отходы
только по таким ценам, при которых оно
получит за них выручку, не меньшую той,
что могло бы получить, организовав
собственное производство.
Эти требования формализуются в виде
следующей ЗЛП.
Требование
1 покупающей организации – минимизация
покупки:
![]() (2.26)
Требование 2
предприятия, реализующего отходы сырья,
можно сформулировать в виде системы
ограничений. Предприятие откажется от
выпуска каждой единицы продукции первого
вида, если
(2.26)
Требование 2
предприятия, реализующего отходы сырья,
можно сформулировать в виде системы
ограничений. Предприятие откажется от
выпуска каждой единицы продукции первого
вида, если ![]() ,
где левая часть означает выручку за
сырьё идущее на единицу продукции
первого вида; правая – её цену.
Аналогичные рассуждения логично провести
в отношении выпуска продукции каждого
вида. Поэтому требование предприятия,
реализующего отходы сырья, можно
формализовать в виде сл. системы
ограничений:
,
где левая часть означает выручку за
сырьё идущее на единицу продукции
первого вида; правая – её цену.
Аналогичные рассуждения логично провести
в отношении выпуска продукции каждого
вида. Поэтому требование предприятия,
реализующего отходы сырья, можно
формализовать в виде сл. системы
ограничений:
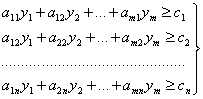 (2.27)
По смыслу задачи
оценки не должны быть
отрицательными:
(2.27)
По смыслу задачи
оценки не должны быть
отрицательными:
![]() .
(2.28)
Переменные
.
(2.28)
Переменные ![]()
![]() называют
двойственными оценками или объективно
обусловленными оценками.
Задачи (2.23) - (2.25) и (2.26) - (2.28) называют
парой взаимно двойственных ЗЛП.
Между прямой и двойственной задачами
можно установить следующую взаимосвязь:
1. Если прямая задача на максимум, то
двойственная к ней — на минимум, и
наоборот.
2.
Коэффициенты
называют
двойственными оценками или объективно
обусловленными оценками.
Задачи (2.23) - (2.25) и (2.26) - (2.28) называют
парой взаимно двойственных ЗЛП.
Между прямой и двойственной задачами
можно установить следующую взаимосвязь:
1. Если прямая задача на максимум, то
двойственная к ней — на минимум, и
наоборот.
2.
Коэффициенты ![]() целевой
функции прямой задачи являются свободными
членами ограничений двойственной
задачи.
3. Свободные
члены
ограничений
прямой задачи являются коэффициентами
целевой функции двойственной.
4. Матрицы ограничений прямой и двойственной
задач являются транспонированными друг
к другу.
5. Если прямая
задача на максимум, то ее система
ограничений представляется в виде
неравенств типа
целевой
функции прямой задачи являются свободными
членами ограничений двойственной
задачи.
3. Свободные
члены
ограничений
прямой задачи являются коэффициентами
целевой функции двойственной.
4. Матрицы ограничений прямой и двойственной
задач являются транспонированными друг
к другу.
5. Если прямая
задача на максимум, то ее система
ограничений представляется в виде
неравенств типа ![]() .
Двойственная задача решается на минимум,
и ее система ограничений имеет вид
неравенств типа
.
Двойственная задача решается на минимум,
и ее система ограничений имеет вид
неравенств типа ![]() .
6. Число ограничений прямой задачи равно
числу переменных двойственной, а число
ограничений двойственной — числу
переменных прямой.
7.
Все переменные в обеих задачах
неотрицательны.
.
6. Число ограничений прямой задачи равно
числу переменных двойственной, а число
ограничений двойственной — числу
переменных прямой.
7.
Все переменные в обеих задачах
неотрицательны.
