Одноканальная смо с ожиданием и его характеристики. Формула Литтла
Система массового обслуживания имеет один канал. Входящий поток заявок на обслуживание - простейший поток с интенсивностью l. Интенсивность потока обслуживания равна m(т. е. в среднем непрерывно занятый канал будет выдавать m. обслуженных заявок). Длительность обслуживания — случайная величина, подчиненная показательному закону распределения. Поток обслуживании является простейшим пуассоновским потоком событий. Заявка, поступившая в момент, когда канал занят, становится в очередь и ожидает обслуживания. Предположим, что независимо от того, сколько требований поступает на вход обслуживающей системы, данная система (очередь+ обслуживаемые клиенты) не может вместить более N-требований (заявок), т. е. клиенты, не попавшие в ожидание, вынуждены обслуживаться в другом месте. Наконец, источник, порождающий заявки на обслуживание, имеет неограниченную (бесконечно большую) емкость. Граф состояний СМО в этом случае имеет вид, показанный на Рис. 3.2.
Рис 3 2 Граф состояний одноканальной СМО с ожиданием (схема гибели и размножения)
Состояния СМО имеют следующую интерпретацию:
S0 - канал свободен
S1 - канал занят (очереди нет);
S2 - канал занят (одна заявка стоит в очереди);
……………………………….
Sn-канал занят (n - 1 заявок стоит в очереди);
……………………………
SN - канал занят (N - 1 заявок стоит в очереди).
Стационарный провес в данной системе будет описываться следующей системой алгебраических уравнений:
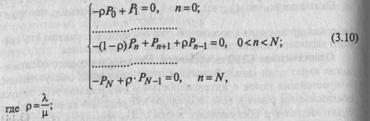
п -номер состояния.
Решение приведенной выше системы уравнений (3.10) для нашей модели СМО имеет вид
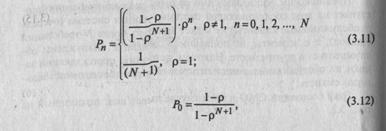
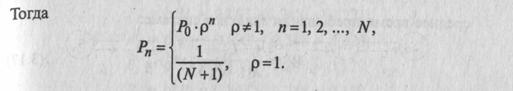
Следует отметить, что
выполнение условия стационарности 
для
данной СМО необязательно, поскольку
число допускаемых в обслуживающую
систему заявок контролируется путем
введения ограничения на длину очереди
(которая не может превышать N—
1), а не соотношением между интенсивностями
входного потока, т. е. не отношением
l/m
= p
Определим характеристики
одноканальной СМОс
ожиданием и ограниченной длиной очереди,
равной (N
—1):
вероятность отказа в обслуживании заявки:
среднее время пребывания заявки в системе:
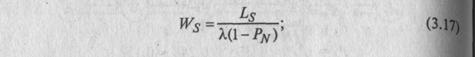
средняя продолжительность пребывания клиента (заявки) в очереди:
среднее число заявок (клиентов) в очереди (длина очереди):
Формула Литтла
Среднее число заявок в системе равно произведению интенсивности входного потока на среднее время пребывания заявки в системе.
Многоканальное смо с ожиданием и ее характеристики. Формула Литтла
Рассмотрим многоканальную СМО (n ? 1) с ожиданием, т. е. заявка, поступившая в СМО в момент времени, когда все каналы заняты, в отличие от СМО с отказами, не покидает систему необслуженной, а становится в очередь и ожидает обслуживания. Следует отметить, что большинство обслуживающих фирм и учреждений устроены как раз по такому принципу. Пусть максимальное число мест в очереди равно т ? 1, т. е. в очереди могут ожидать своего обслуживания не более т заявок. Поэтому заявка, пришедшая на вход в СМО в момент, когда в очереди уже находятся т заявок, получает отказ и покидает систему. Иными словами, «заполнение» СМО заявками из входного потока идет в два этапа: сначала происходит загрузка каналов обслуживания, затем заполняется очередь. Нумерация состояний системы в этом случае имеет следующий вид: от состояния s0 (в СМО нет заявок и все каналы свободны) до состояния sn (в СМО n заявок и все каналы заняты) очереди нет; от состояния sn+1 (в СМО n + 1 заявка, все каналы заняты и одна заявка находится в очереди) до состояния sn + m(все каналы заняты и все т мест в очереди заняты заявками) происходит заполнение очереди.
Граф
состояний СМО показан на рис. 2. Переход
системы из состояния sk в состояние sk+1
слева направо (k = 0, 1,..., n + т - 1) происходит
под воздействием одного и того же
входного потока заявок интенсивности
, следовательно, плотности вероятности
перехода из состояния в состояние слева
направо одинаковы и равны
.
Переход системы из состояния
в состояние справа налево происходит
с разными плотностями вероятностей
внутри двух циклов состояний, отмеченных
выше. Если заявка продолжает оставаться
в очереди (состояние sk, n+1?k?n+т), т.
е. все каналы заняты, то эти переходы
имеют плотность вероятности,
равную n 
(перемещение
системы из состояния в состояние
обусловлено общей работой nканалов).
Если система находится в состоянии,
когда занято k каналов
(1 ? k
? n ), то
переход ее в левое состояние обусловлен
потоком, представляющим собой
сумму k потоков
обслуживании (общей работой k каналов);
в таком случае плотность вероятности
перехода равна k
.
Следует
отметить, что система не может
«перескакивать» через промежуточное
состояние, а переходит из состояния в
состояние последовательно: либо слева
направо, либо справа налево по графу
состояний.
Предельные вероятности р0, р1,..., рn, рn+1, ..., рn+т соответствующих состояний СМО удовлетворяют системе линейных однородных алгебраических уравнений, которая получается из системы дифференциальных уравнений Колмогорова путем, аналогичным описанному выше. Эта система имеет вид:
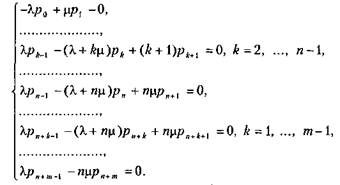
К этой системе уравнений необходимо добавить нормировочное условие
Введем величину 
= р/n =
/(n
) -
показатель нагрузки на один канал. Решение
системы уравнений выражается, как и в
случае СМО с отказами, через вероятность
простоя системы (или вероятность того,
что все каналы свободны) р0:
Второе слагаемое в правой
части этого равенства является
суммой т членов
геометрической прогрессии с первым
членом 
изнаменателем
,
т. е. формула для р0 упрощается:
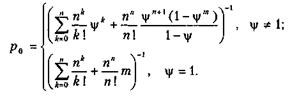
Остальные предельные вероятности состояний имеют вид, аналогичный формулам:
Характеристики СМО
Вероятность
отказа (заявка, поступившая в момент,
когда заняты все n каналов
и все т мест
в очереди) есть вероятность того, что
СМО находится в состоянии sn+m, откуда
получаем:
Так как события отказа заявки и приема ее в СМО являются противоположными, то вероятность приема заявки в СМО равна вероятности psys и относительной пропускной способности системы:
Отсюда получаем формулу для абсолютной пропускной способности:
Так как каждый занятый канал обслуживает в среднем ц заявок в единицу времени, то среднее число заявок, находящихся под обслуживанием (или среднее число занятых каналов) подсчитывается по формуле:
Для вычисления среднего
числа заявок 
line, находящихся
в очереди, рассмотрим дискретную
случайную величину Nline, —
число заявок в очереди. Закон
распределения Nline имеет
вид:
Nline |
0 |
1 |
2 |
… |
т |
Р |
Ps |
Рп+1 |
Рп + 2 |
… |
Рп + т |
Здесь
,
поскольку событие, состоящее в том, что в очереди нет ни одной заявки, является объединением событий, состоящих в том, что СМО находится в одном из состояний s0, s1..., sn. Так как lineявляется математическим ожиданием М случайной величины Nline;, то отсюда получаем и преобразуем:
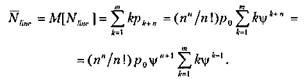
Сумма в последнем равенстве
имеет выражение в виде компактной
формулы как при 
(формула
суммирования), так и при 
(сумма
отрезка натурального ряда чисел).
Соответственно мы получаем окончательное
выражение для среднего числа заявок в
очереди:
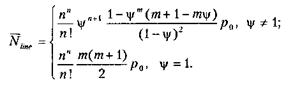
Среднее число заявок, находящихся в системе, равно сумме средних чисел обслуживаемых заявок и заявок, находящихся в очереди:
Для средних величин времени обслуживания заявки, времени ожидания заявки в очереди и времени пребывания заявки в системе имеем, соответственно, следующие формулы (формулы Литтла):
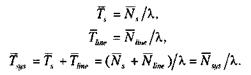
Выше названные формулы позволяют рассчитать все характеристики работы многоканальной СМО с ожиданием и ограничением на длину очереди. Эти формулы используются для проверки результатов моделирования.