Министерство образования Российской Федерации

Казанский государственный технический университет им. А.Н.Туполева

Лабораторный практикум

По гидравлике

Казань 2002

Работа 1

Исследование потока жидкости в канале переменного сечения

I. Цель работы

• определение давлений и среднерасходных скоростей жидкости в трех сечениях канала с горловиной;

• вычисление полных давлений в трех сечениях канала с горловиной;

• построение графиков изменения скорости, статического давления и полного давления по длине канала.

II. Теоретические основы

Для решения задач механики жидкости и газа используются уравнения основных законов природы – закона сохранения массы, закона сохранения энергии и других. Их записывают для выделенного объема, сквозь который протекает жидкость, в такой форме, чтобы отразить специфику изучаемой материальной среды.

При движении жидкости по трубе через поперечное сечение трубы в единицу времени протекает масса жидкости, равная произведению  u F.

Это произведение называется массовым расходом и обозначается буквой G. Здесь , u – плотность и скорость жидкости соответственно, F – площадь поперечного сечения трубы (канала).

Закон сохранения массы математически выражается уравнением неразрывности (расхода), которое для канала переменного сечения (рис.1) при установившемся движении жидкости имеет вид

(1)

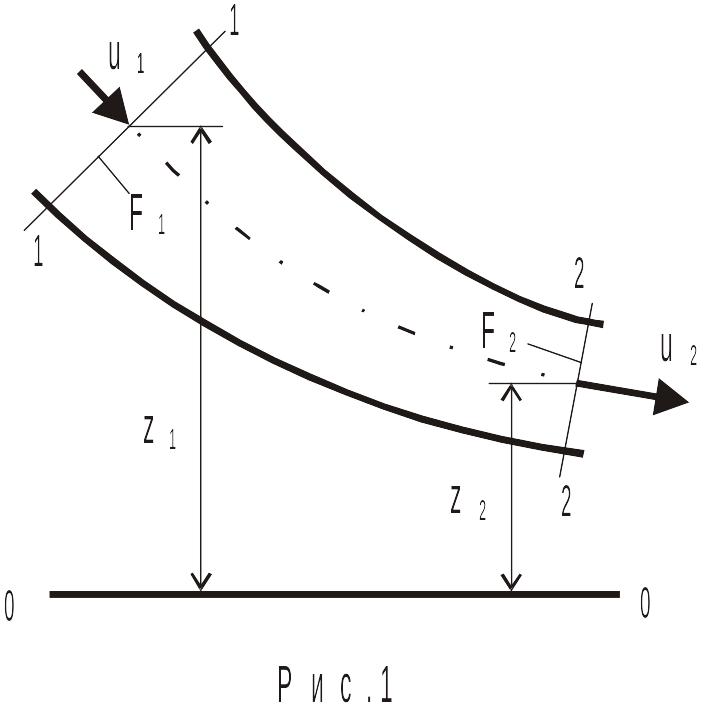У равнение (1) говорит о том, что, какая масса жидкости втекает в единицу времени в канал, такая же и протекает в единицу времени через любое другое поперечное сечение канала с непрони-цаемыми стенками, т.е. вдоль канала выполняется условие постоянства расхода:

G = ρuF = const (2)

Можно сказать, что при установившемся движении сколько жидкости втекает в канал, столько же и вытекает из него в единицу времени.

Д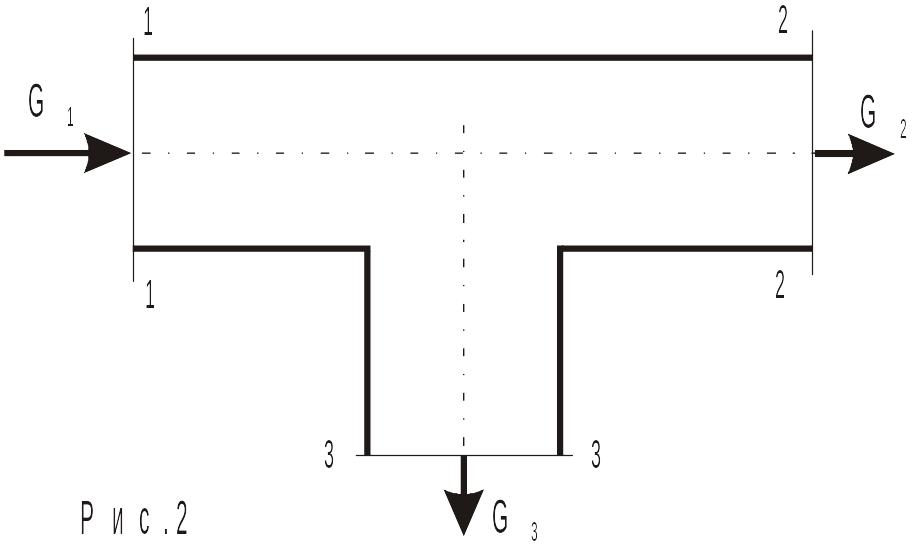 ля разветвленного канала, как, например, на рисунке 2, уравнение неразрывности записывается в таком виде

G₁=G₂+G₃ (3)

Если жидкость несжимаема, то есть, ρ = const, уравнения (1), (2) и (3) можно поделить на плотность ρ и записать следующим образом

u₁ F₁ = u₂ F₂ (4)

Q = u F = const (5)

Q₁ = Q₂+ Q₃ (6)

Произведение Q = uF представляет собой объем жидкости, протекающей через поперечное сечение канала в единицу времени, и называется объемным расходом. Его размерность в системе СИ – м³/с. Для несжимаемой жидкости из уравнений (4) и (5) следует, что в канале переменного сечения скорость изменяется обратно пропорционально площади поперечного сечения канала.

При записи уравнений (4) и (5) предполагается, что скорости всех частиц жидкости в сечении одинаковы во всех его точках. Для вязкой жидкости это не так, поскольку вследствие прилипания скорость жидкости на стенке неподвижного канала равна нулю и отлична от нуля в других точках сечения. Поэтому объемный расход нужно вычислять как интеграл

Для того, чтобы можно было пользоваться простыми и удобными уравнениями (4) и (5) вводят понятие среднерасходной скорости

.

Закон сохранения и превращения энергии для участка 1-2 (см.рис.1) потока вязкой несжимаемой жидкости записывается в виде уравнения Д.Бернулли

(7)

В этом уравнении каждый член имеет размерность давления и представляет собой энергию, приходящуюся на единицу объема жидкости (удельную энергию):

• ρgz – удельная потенциальная энергия положения; координата z отсчитывается от выбираемой произвольно горизонтальной плоскости (плоскости сравнения 0-0; см. рис.1);

• p – удельная потенциальная энергия давления (статическое давление);

• ρu²/2 – удельная кинетическая энергия (скоростное, динамическое давление);

•  p_r – потеря механической энергии единицы объема жидкости между сечениями 1 и 2.

Входящие в уравнение коэффициенты Кориолиса α₁ и α₂ учиты-вают неравномерность распределения скорости в сечениях 1 и 2, так что в формуле (7) u – среднерасходная скорость. Для ламинарного течения α= 2, для турбулентного обычно принимают α = 1.

Если канал расположен горизонтально, то z₁= z₂, и уравнение (7) для турбулентного течения принимает вид

(8)

Величину называют давлением торможения, полным давлением, давлением заторможенного потока.

Потерю механической энергии  p_r можно выразить из (8) в виде разности полных давлений: , поэтому  p_r часто называют потерей полного давления. Величина потерь зависит от формы проточной части канала, его длины, режима течения и шероховатости омываемых жидкостью стенок. Потери полного давления обусловлены вязкостью жидкости.

В

Рис.3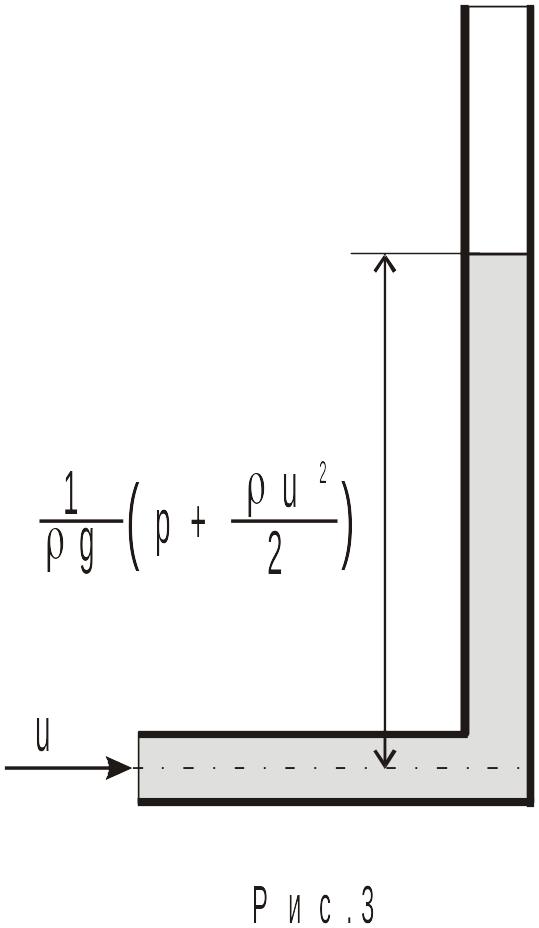

экспериментальных исследова-ниях давление торможения обычно измеряют с помощью специальной тонкой трубочки, трубки Пито, вводимой в поток (рис.3). Плоскость отверстия этой трубочки, в которое затекает жидкость, располагается перпенди-кулярно вектору скорости набегающего потока, поэтому показание прибора, присоеди-ненного к трубке Пито, включает в себя и скоростное давление. В случае, когда введение трубки Пито в поток затруднительно, например, в силу малых размеров сечения, давление торможения вычисляют, используя результаты других измерений.

Р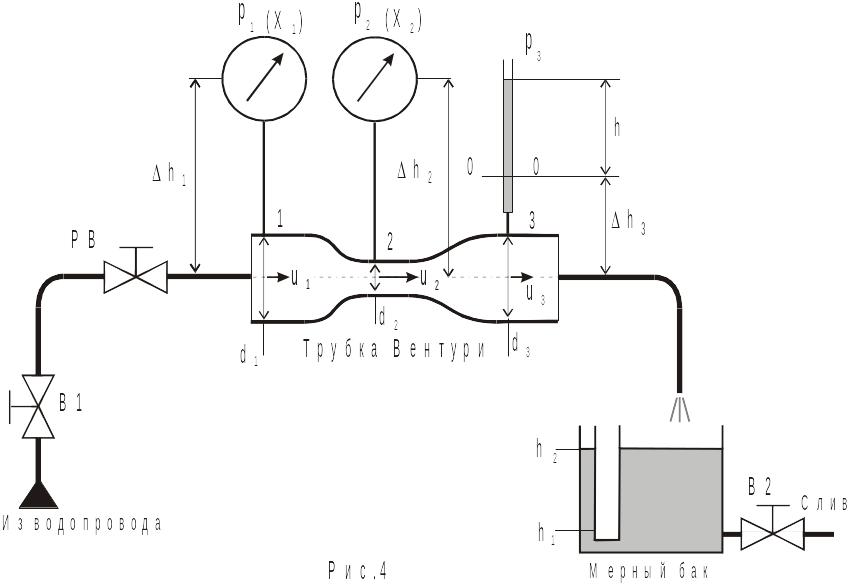 ассмотрим течение в канале с горловиной – трубке Вентури (рис.4). В этом канале согласно уравнению расхода (4) скорость жидкости изменяется обратно пропорционально площади сечения, т.е., возрастает от сечения 1 до сечения 2, а затем уменьшается от сечения 2 до сечения 3. Статическое давление изменяется в соответствии с уравнением Бернулли: уменьшается с ростом скорости и увеличивается при ее уменьшении. Давление торможения вдоль трубки уменьшается вследствие действия вязкости (наличия потерь). Его можно вычислить по результатам измерения статических давлений в выбранных сечениях и расхода жидкости при известных площадях выбранных сечений.

Запишем уравнения расхода и Бернулли для сужающегося и расширяющегося участков. Будем иметь:

сужение 1 – 2: ;

расширение 2 – 3: .

Вычислив скорость как u=Q/F, можно подсчитать давление торможения

и определить потери как разницу полных давлений

.

В случае, когда площади входа и выхода одинаковы, u₃ = u₁ , потери давления на трубке равны разности статических давлений на входе в трубку и на выходе из нее:

_.

Это можно показать, записывая уравнение Бернулли (8) для сечений 1 – 3 (вход и выход из трубки Вентури).