Лямин К.В. М 390502

Министерство образования и науки Российской Федерации

Федеральное государственное автономное образовательное учреждение

высшего профессионального образования

«Уральский федеральный университет

имени первого Президента России Б.Н. Ельцина»

Механико-машиностроительный институт

:

Реферат

Обработка зубчатых колес

Руководитель	С.Ю.Маталасов
Студент гр. М390502	К.В. Лямин

2012

Содержание.

Зубчатые передачи классифицируются по признакам, приведенным ниже. 4

Контроль зубчатых колес 7

Рис.5.Длина общей нормали. 7

Эвольвентное зацепление. 8

Технология изготовления зубчатых колёс. 8

Базирование. 9

Технологические задачи 12

Обработка заготовки зубчатых колес до нарезания зубьев. 14

Основные методы формообразования зубьев зубчатых колес 15

Отделочные виды обработки зубчатых колес. 19

Эвольвента окружности.

Геометрическое место центров кривиз­ны какой-либо кривой называется эволютой, а сама кривая по от­ношению к эволюте — разверткой или эвольвентой. Следователь­но, эвольвента окружности есть кривая, центры кривизны которой лежат на окружности. Эвольвента (для краткости в дальнейшем опускаем слово «окружно­сти») может быть получена как траектория точки пря­мой, перекатывающейся без скольжения по окружности. В теории зацепления окруж­ность, эвольвентой которой является профиль зуба, на­зывается основной окруж­ностью.

Н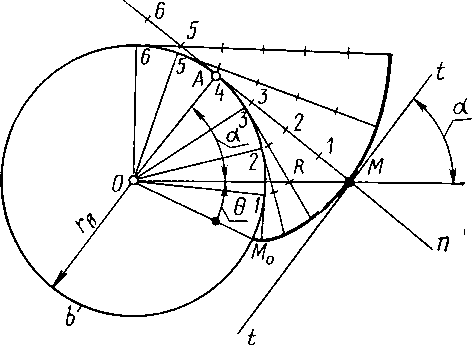 а рисунке 1 показано пос­троение эвольвенты основ­ной окружности b при пере­катывании по ней прямой, называемой произво­дящей прямой. Пусть производящая прямая показана в положении, когда она касается основной окружности в точке А и надо построить эвольвенту, опи­сываемую точкой М. Делим отрезок AM на равные части (напри­мер, на четыре части) и откладываем на основной окружности дуги, равные соответствующим частям отрезка AM: 43=43, 32=32, и т. д. (при малых центральных углах дуги можно заменять хор­дами). Через полученные точки деления окружности проводим к ней касательные и откладываем на них отрезки, последовательно уменьшая длину каждого отрезка на одну часть. Например, из точ­ки 3 откладываем отрезок, содержащий три части, из точки 2 — две части и т. д. Соединяя концы отложенных отрезков, получаем эвольвенту.

Е

Рис.1.

сли нужно продолжить эвольвенту, то на производящей пря­мой откладывают отрезки 45=56 и т. д., а на окружности — дуги 45, 56, равные по длине отрезкам 45, 56. Для построения точек эвольвенты из точки 5 проводят касательную к основной окружно­сти и на ней откладывают отрезок, содержащий пять частей, и т. д.

З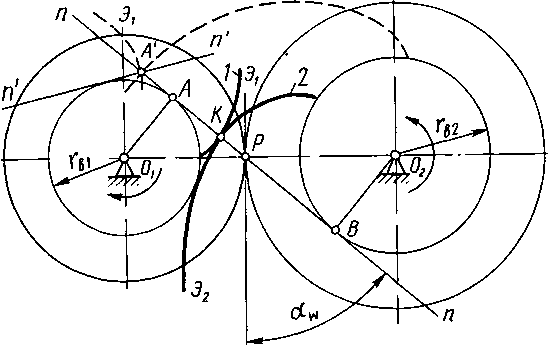 аметим также, что эвольвенту можно представить как траек­торию точки М конца нити, которая в натянутом положении нама­тывается на барабан, диаметр которого равен диаметру основной окружности.

Рис.2.

Зубчатые передачи классифицируются по признакам, приведенным ниже.

По взаимному расположению осей колес (Рис. 4.): с параллельными осями (цилиндрическая передача, I—IV); с пересекающимися осями (коническая передача, V, VI); со скрещивающимися осями (винтовая передача, VII; червячная передача, VIII).

- В зависимости от относительного вращения колес и расположения зубьев различают передачи с внешним и внутренним зацеплением. В первом случае (I—III) вращение колес происходит в противоположных направлениях, во втором (IV) — в одном направлении. Реечная передача ( IX) служит для преобразования вращательного движения в поступательное.

- По форме профиля различают зубья эвольвентные (I, II) и неэвольвентные, например цилиндрическая передача Новикова, зубья колес которой очерчены дугами окружности.

- В зависимости от расположения теоретической линии зуба различают колеса с прямыми зубьями (I), косыми (II), шевронными (III) и винтовыми (IV). В непрямозубых передачах возрастает плавность работы, уменьшается износ и шум. Благодаря этому непрямозубые передачи большей частью применяют в установках, требующих высоких окружных скоростей и передачи больших мощностей.

- По конструктивному оформлению различают закрытые передачи, размещенные в специальном непроницаемом корпусе и обеспеченные постоянной смазкой из масляной ванны, и открытые, работающие без смазки или периодически смазываемые консистентными смазками.

- По величине окружной скорости различают: тихоходные передачи (v равной до 3 м/с), среднескоростные (v равной от 3... 15 м/с) и быстроходные (v более 15 м/с).

Зубчатые передачи с зацеплением M.Л. Новикова

В этом зацепле­нии профиль зубьев выполняется не по эвольвенте, а по дуге окружности (Рис.3.) или по кривой, близкой к ней.

При зацеплении выпуклые зубья одного из колес контактируют с вогнуты­ми зубьями другого. Поэтому площадь соприкосновения одного зуба с другим в передаче Новикова значительно больше, чем в эвольвентных передачах. Касание сопряженных профилей теоретически происходит в точке, поэтому данный вид зацепления называют точечным.

П

Рис.3.

ри одинаковых с эвольвентным зацеплением параметрах точечная систе­ма зацепления с круговым профилем зуба обеспечивает увеличение контакт­ной прочности, что в свою очередь позволяет повысить нагрузочную способ­ность передачи в 2...3 раза по сравнению с эвольвентной. Взаимодействие зу­бьев в сравниваемых передачах также ййййййййййййййййййй различно: в эвольвентном зацеплении преобладает скольжение, а в зацеплении Новикова — качение. Это создает благоприятные условия для увеличения масляного слоя между зубьями, уменьшения потерь на трение и увеличения сопротивления заеданию.

К

Рис.3.

достоинствам зацепления Новикова относятся возможность применения его во всех видах зубчатых передач: с параллельными, пересекающи­мися и скрещивающимися осями колес, с внешним и внутренним зацеплением, постоянным и переменным передаточным отношением. Потери на трение в этой системе зацепления примерно в 2 раза меньше потерь в эвольвентном зацеплении, что увеличивает КПД передачи.

К основным недостаткам передач с зацеплением Новикова относятся: технологическая трудоемкость изготовления колес, ширина колес должна быть не менее 6 модулей и др. В настоящее время передачи с зацеплением Новикова находят применение в редукторах больших размеров.

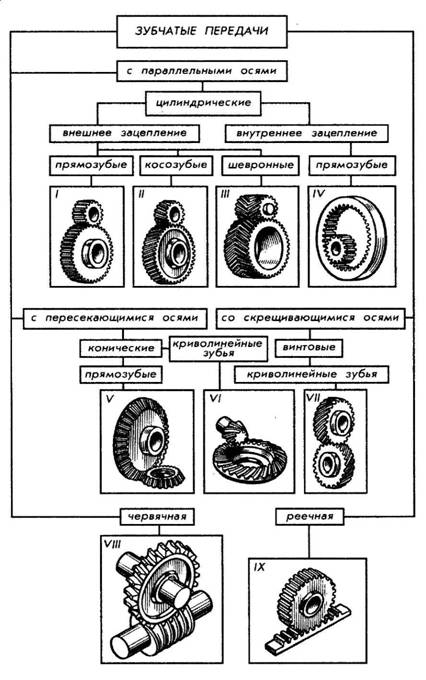
Рис.4. Типы зубчатых передач

Контроль зубчатых колес

Контроль элементов зуба и зацепления зубчатых колес производят согласно ГОСТ. Приборы контроля можно разделить на три группы: с записывающими устройствами (самописцами) для непрерывной записи погрешностей вдоль всего профиля зуба; для контроля нескольких параметров (эвольвенты, направления зуба, ошибки шага и радиального биения); с механическим приводом (измерение происходит автоматически, а установка и снятие измерительного зубчатого колеса — вручную).

Для контроля эвольвенты, направления зуба, ошибок шага и радиального биения зубчатого венца применяется универсальный прибор с записывающим устройством. На приборе измеряют прямозубые, косозубые, червячные и зубчатые колеса с внутренним зацеплением модулем до 12 мм и диаметром до 500 мм.

Для комплексной двухпрофильной проверки используют универсальные приборы с индикатором или записывающим устройством. Проверяют изменение измерительного межцентрового расстояния за один оборот колеса. Измеряемое и эталонное зубчатые колеса находятся в беззазорном зацеплении. Погрешности проверяемого колеса изменяют межцентровое расстояние этих колес, и при их взаимном вращении происходит перемещение плавающей каретки прибора. С кареткой связано перо устройства, записывающего колебания межцентрового расстояния. Устройство приводится во вращение от контролируемого колеса через ременную передачу и диски трения.

Для измерения уровня шума используют контрольно-обкатные станки, снабженные осциллографом, на экране которого регистрируются шумовые характеристики проверяемого зубчатого колеса. Величина допустимого уровня шума ограничена верхним и нижним пределами.

Окончательный контроль конических колес с винтовыми зубьями (например, ведомого колеса главной пары заднего моста) осуществляется на станках «Глиссон» в специальной кабине с эталонным ведущим колесом на шум, пятно контакта и боковой зазор.

Д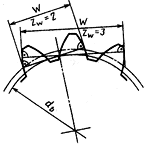 лина общей нормали зубчатого колеса (W) длина общей нормали. Расстояние между разноименными боковыми поверхностями зубьев цилиндрического зубчатого колеса по общей нормали к этим поверхностям.

Рис.5.Длина общей нормали.

Эвольвентное зацепление.

Пусть профиль зуба звена 1 очерчен по эвольвенте основной окружности с радиусом r_b1, а про­филь зуба звена 2 — по эвольвенте основной окружности с ради­усом r_b2. Поместим центры этих окружностей в центры вращения 0₂ и 0₁ и приведем эвольвенты в соприкасание в точке K Нормаль к эвольвенте Э₁ в точке К должна быть касательной к основной окружности звена 1, а нормаль к эвольвенте Э₂ — касательной к основной окружности звена 2. В точке касания нормаль должна быть общей к обоим профилям, и, следовательно, точка К лежит на общей касательной к основным окружностям. При вращении звеньев 1 и 2 точка касания эвольвент перемещается по отрезку АВ этой касательной, так как вне отрезка АВ эвольвенты не могут касаться, т. е. иметь общую нормаль. Например, для точки А' нор­маль к эвольвенте Э₁ направлена по линии n'n', а к эвольвенте Э₂ — по линии nn. Геометрическое место точек контакта сопря­женных профилей (в рассматриваемом примере — отрезок АВ) называется линией зацепления.

Точка пересечения общей нормали к эвольвентам с межосевой линией (Р — полюс зацепления) занимает неизменное положение, и, следовательно, согласно основной теореме зацепления переда­точное отношение u₂₁ имеет постоянную величину

u₂₁ = ±r_w1/ r_w2,

где r_w1 = l_01p и r_w2 =l_02p — радиусы начальных окружностей. Знак плюс относится к внутреннему зацеплению, а знак минус — к внешнему.

Угол между линией зацепления и прямой, перпендикулярной межосевой линии, называется углом зацепления и обозна­чается через а_w. Из треугольников 0₁АР и 0₂ВР следует

r_b1= r_w1cosa_w и r_b2= r_w2cosa_w

Следовательно, при эвольвентном зацеплении передаточное отно­шение может быть также выражено через отношение радиусов ос­новных окружностей:

u₂₁ = ±r_b1/ r_b2,

Из видно, что при эвольвентном зацеплении изменение межосевого расстояния не влияет на передаточное отношение вследствие неизменности радиусов основных окружностей. При изменении межосевого расстояния изменяются лишь радиусы на­чальных окружностей и угол зацепления.