
- •Задача о массе стержня II. Задача о пройденном пути III. Задача о площади криволинейной трапеции
- •2. G(X) монотонна и ограничена: .
- •1 3.4.2. Объём тела, получающегося при вращении кривой вокруг координатной оси. Если объём получается в результате вращения кривой , , вокруг оси , то, очевидно, , поэтому .
- •О пределение двойного интеграла для прямоугольника
- •Свойства двойного интеграла.
П![]() ервообра́зной [1] или примити́вной
функцией (иногда называют
также антипроизводной)
данной функции f называют
такую F, производная которой
(на всей области определения) равна f,
то есть F ′ = f. Вычисление
первообразной заключается в нахождении
неопределённого интеграла, а сам процесс
называется интегрированием.Так,
например, функция
ервообра́зной [1] или примити́вной
функцией (иногда называют
также антипроизводной)
данной функции f называют
такую F, производная которой
(на всей области определения) равна f,
то есть F ′ = f. Вычисление
первообразной заключается в нахождении
неопределённого интеграла, а сам процесс
называется интегрированием.Так,
например, функция ![]() является
первообразной
является
первообразной ![]() семейство первообразных
функции x2 можно обозначить как F(x)
= x3 / 3 + C, где C — любое
число. Графики таких
первообразных смещены вертикально
относительно друг друга, и их положение
зависит от значения C.Первообразные
важны тем, что позволяют вычислять интегралы.
Если F — первообразная нтегрируемой
функции f, то:Это соотношение
называется формулой
Ньютона — Лейбница.Благодаря этой
связи множество первообразных данной
функции f называют неопределённым
интегралом (общим интегралом)
семейство первообразных
функции x2 можно обозначить как F(x)
= x3 / 3 + C, где C — любое
число. Графики таких
первообразных смещены вертикально
относительно друг друга, и их положение
зависит от значения C.Первообразные
важны тем, что позволяют вычислять интегралы.
Если F — первообразная нтегрируемой
функции f, то:Это соотношение
называется формулой
Ньютона — Лейбница.Благодаря этой
связи множество первообразных данной
функции f называют неопределённым
интегралом (общим интегралом)
Теорема. Если F1 (x) и F2 (х)- две первообразные от функции f(x) на отрезке [a,b], то разность между ними равна постоянному числу.
Доказательство. В силу определения первообразной имеем F1 ′(х)= f(x), F2 ′(х)= f(x) (1)При любом значении х на отрезке [a,b].Обозначим F1 (х)- F2 (х) =φ(х) (2)
Тогда на основании равенств (1) будет F′1 (х)- F′2 (х)= f(x)- f(x)=0 или φ′(х)=[ F′1 (х)- F′2 (х)]′≡0 при любом значении х на отрезке [a,b]. Но из равенства φ′(х)=0 следует, что φ(х) есть постоянная. Действительно, применим теорему Лагранжа к функции φ(х), которая, очевидно, непрерывна и дифференцируема на отрезке [a,b]. Какова бы ни была точка х на отрезке [a,b], мы имеем в силу теоремы Лагранжа φ(х)- φ(а)= (х-а) φ′(z), где а < z < x.Так как φ′(z)=0, то φ(х)- φ(а)=0, или φ(х)= φ(а). (3)
Таким образом, функция φ(х) в любой точке х отрезка [a,b] сохраняет значение φ(а), а это значит, что функция φ(х) является постоянной на отрезке [a,b]. Обозначая постоянную φ(а) через С, из равенств (2) и (3) получаем F1 (х)- F2 (х) = С.
Из доказанной теоремы следует, что если для данной функции f(x) найдена какая- нибудь одна первообразная F(x), то любая другая первообразная для f(x) имеет вид F(x)+ С, где С = const/
Неопределённый
интегра́л для функции ![]() -
это совокупность всех первообразных данной
функции.
-
это совокупность всех первообразных данной
функции.
Св1. Постоянный
множитель можно вынести за знак
интеграла:![]()
Св2. Интеграл
алгебраической суммы равен алгебраической
сумме интегралов:![]() Первые
два свойства выражают линейность интеграла.
Первые
два свойства выражают линейность интеграла.
Св 4.3. Вид
интеграла не зависит от вида переменной
интегрирования:![]() (4.12)или,
что тоже самое,
(4.12)или,
что тоже самое,![]() (4.12')где
(4.12')где ![]() —
непрерывная вместе со своей производной
функция.
—
непрерывная вместе со своей производной
функция.
Св4. Имеет
место следующее равенство:![]() (4.42)
(4.42)
где u и v — две непрерывно дифференцируемые функции
Св 4.1. Постоянный
множитель можно вынести за знак
интеграла:
(4.4)Продифференцируем
левую и правую части равенства,
получим:![]() и
и ![]() (4.5)
(4.5)
В
левой части по формуле (2.8) получаем:![]() (4.6)в
правой части по правилам
дифференцирования получаем:
(4.6)в
правой части по правилам
дифференцирования получаем:![]() (4.7)
(4.7)
Воспользовавшись
снова (2.8) окончательно получаем:![]() (4.8Равенство
правой и левой частей доказывает
рассматриваемое свойство.
(4.8Равенство
правой и левой частей доказывает
рассматриваемое свойство.
Интегрирование
по частям. Пусть
![]() -
дифференцируемые функции, тогда
справедлива формула:
-
дифференцируемые функции, тогда
справедлива формула:
![]() ,
или короче:
,
или короче:
![]() .
Эта формула используется в тех случаях,
когда подынтегральное выражение
.
Эта формула используется в тех случаях,
когда подынтегральное выражение
![]() можно
так представить в виде
можно
так представить в виде
![]() ,
что интеграл
,
что интеграл
![]() вычисляется
проще исходного.
вычисляется
проще исходного.
Пример:
Вычислить
![]() .
.
Положим
![]() .
Тогда
.
Тогда
![]() .
В качестве
.
В качестве
![]() выберем
первообразную при
выберем
первообразную при
![]() .
Получим
.
Получим
![]() .
Снова
.
Снова
![]() .
Тогда
.
Тогда
![]() .
Окончательно получим:
.
Окончательно получим:
![]() .
Замечание
26.5: Иногда при вычислении интеграла
.
Замечание
26.5: Иногда при вычислении интеграла
![]() методом
интегрирования по частям получается
зависимость:
методом
интегрирования по частям получается
зависимость:
![]() .
Откуда можно получить выражение для
первообразной:
.
Откуда можно получить выражение для
первообразной:
![]() .
.
Задача о массе стержня II. Задача о пройденном пути III. Задача о площади криволинейной трапеции
Пусть на замкнутом промежутке [a, b] задана функция f(x). Проделаем следующие операции:
Раздробим [a, b] на части точками x0 = a < x1 < x2 < ... < xn-1 < xn = b, причем наибольшую из разностей xk+1 - xk обозначим через λ. 2) В каждом частичном промежутке [xk, xk+1] выберем по точке ξk и вычислим f(ξk). 3) Умножим f(ξk) на длину (xk+1 - xk) соответствующего промежутка [xk, xk+1].
Сложим
все найденные произведения. Сумму ![]()
![]()
![]() будем
называть интегральной суммой.5) Будем
изменять произведённое дробление [a, b]
так, чтобы величина λ стремилась
к нулю. Если при этом существует
конечный предел
будем
называть интегральной суммой.5) Будем
изменять произведённое дробление [a, b]
так, чтобы величина λ стремилась
к нулю. Если при этом существует
конечный предел ![]()
![]() (4)не зависящий от выбора точек ξk, то
этот предел называется определенным
интегралом от функции f(x) по
промежутку [a, b] и обозначается через
(4)не зависящий от выбора точек ξk, то
этот предел называется определенным
интегралом от функции f(x) по
промежутку [a, b] и обозначается через![]()
![]()
Т еорема
существования определённого интеграла. Если
функция f(x) непрерывна на
отрезке [a,b], то она интегрируема по
этому отрезку.
еорема
существования определённого интеграла. Если
функция f(x) непрерывна на
отрезке [a,b], то она интегрируема по
этому отрезку.
![]() Примем
это утверждение без доказательства,
поясним только его смысл. Интегрируемость
функции означает существование конечного
предела последовательности интегральных
сумм, т.е. такого числа
Примем
это утверждение без доказательства,
поясним только его смысл. Интегрируемость
функции означает существование конечного
предела последовательности интегральных
сумм, т.е. такого числа 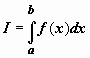 ,
что для любого
,
что для любого ![]() найдётся
такое число
найдётся
такое число ![]() ,
что как только разбиение отрезка
удовлетворяет неравенству
,
что как только разбиение отрезка
удовлетворяет неравенству ![]() ,
то, независимо от выбора точек
,
то, независимо от выбора точек ![]() выполняется
неравенство. Требование
непрерывности f(x) достаточно для
интегрируемости, но не является
необходимым. Интегрируемы функции,
имеющие конечное или даже счётное число
точек разрыва на [a,b] при условии
их ограниченности (т.е. все точки разрыва
должны быть точками разрыва первого
рода). Неограниченная функция не может
быть интегрируемой (идея доказательства
этого утверждения: если f(x) неограничена
на [a,b], то она неограничена на
каком-либо [xi-1 , xi], т.е. на этом
отрезке можно найти такую точку
,
что слагаемое
выполняется
неравенство. Требование
непрерывности f(x) достаточно для
интегрируемости, но не является
необходимым. Интегрируемы функции,
имеющие конечное или даже счётное число
точек разрыва на [a,b] при условии
их ограниченности (т.е. все точки разрыва
должны быть точками разрыва первого
рода). Неограниченная функция не может
быть интегрируемой (идея доказательства
этого утверждения: если f(x) неограничена
на [a,b], то она неограничена на
каком-либо [xi-1 , xi], т.е. на этом
отрезке можно найти такую точку
,
что слагаемое ![]() ,
а следовательно, и вся интегральная
сумма, будет больше любого наперед
заданного числа).
,
а следовательно, и вся интегральная
сумма, будет больше любого наперед
заданного числа).
. Геометрический смысл определённого интеграла. Как следует из пункта 11.1.1, если f(x) >0 на отрезке [a,b], то равен площади криволинейной трапеции ABCD, ограниченной снизу отрезком [a,b], слева и справа - прямыми x = a и x = b, сверху – функцией y = f(x).
5. Теоремы об оценке интеграла.
5.1.
Если на отрезке
![]() функция удовлетворяет неравенству
функция удовлетворяет неравенству
![]() ,
то
,
то
![]() .
.
Док-во.
Докажем левое неравенство (цифрами над
знаками импликации обозначены номера
применяемых ранее доказанных свойств):
![]() .
Аналогично доказывается и правое
неравенство.
.
Аналогично доказывается и правое
неравенство.
5.2.
Если функция
![]() интегрируема по отрезку
,
то
интегрируема по отрезку
,
то
![]() .
.
Док-во.
![]() .
.
8.
Теорема о среднем. Если
непрерывна на отрезке
,
то существует точка
![]() ,
такая что
,
такая что
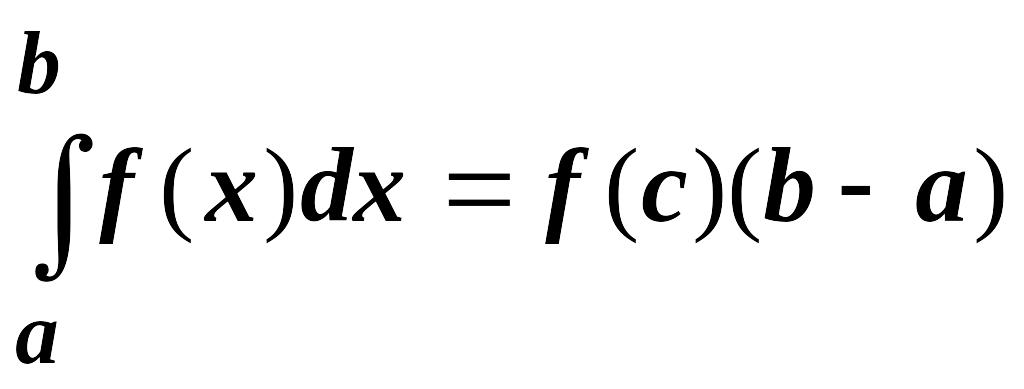 .
Док-во. Функция, непрерывная на отрезке,
принимает на этом отрезке своё наименьшее
.
Док-во. Функция, непрерывная на отрезке,
принимает на этом отрезке своё наименьшее
![]() и наибольшее
и наибольшее
![]() значения. Тогда
значения. Тогда
![]() .
Число
.
Число
![]() заключено между минимальным и максимальным
значениями функции на отрезке. Одно из
свойств функции, непрерывной на отрезке,
заключается в том, что эта функция
принимает любое значение, расположенное
между
и
.
Таким образом, существует точка
,
такая что
заключено между минимальным и максимальным
значениями функции на отрезке. Одно из
свойств функции, непрерывной на отрезке,
заключается в том, что эта функция
принимает любое значение, расположенное
между
и
.
Таким образом, существует точка
,
такая что
![]() .
.
Это
свойство имеет простую геометрическую
интерпретацию: если
![]() непрерывна на отрезке
,
то существует точка
такая, что площадь криволинейной трапеции
непрерывна на отрезке
,
то существует точка
такая, что площадь криволинейной трапеции
![]() равна площади прямоугольника с основанием
и высотой
равна площади прямоугольника с основанием
и высотой
![]() (на
рисунке выделен цветом).
(на
рисунке выделен цветом).
![]() Формула
Ньютона-Лейбница. Если
непрерывна на отрезке
,
и
Формула
Ньютона-Лейбница. Если
непрерывна на отрезке
,
и
![]() -
некоторая первообразная функции
,
то
-
некоторая первообразная функции
,
то
![]() . Док-во.
Мы установили, что функция
. Док-во.
Мы установили, что функция
![]() - первообразная непрерывной
.
Так как
- тоже первообразная, то
- первообразная непрерывной
.
Так как
- тоже первообразная, то
![]() .
Положим в этом равенстве
.
Положим в этом равенстве
![]() .
Так как
.
Так как
![]() ,
то
,
то
![]() .
В равенстве
.
В равенстве
![]() переобозначим переменные: для переменной
интегрирования
переобозначим переменные: для переменной
интегрирования
![]() вернёмся
к обозначению
вернёмся
к обозначению
![]() ,
верхний предел
обозначим
,
верхний предел
обозначим
![]() .
Окончательно,
.Разность
в правой части формулы Нь-Ле обозначается
специальным символом:
.
Окончательно,
.Разность
в правой части формулы Нь-Ле обозначается
специальным символом:
![]() (здесь
(здесь
![]() читается как "подстановка от
читается как "подстановка от
![]() до
"),
формулу Ньа-Лей обычно записывают так:
до
"),
формулу Ньа-Лей обычно записывают так:
![]() .
Пример применения формулы НЛей:
.
Пример применения формулы НЛей:
![]() .
.
Ф ормула
интегрирования по частям для определённого
интеграла. Если
ормула
интегрирования по частям для определённого
интеграла. Если
![]() - непрерывно дифференцируемые функции,
то
- непрерывно дифференцируемые функции,
то
![]() .
Док-во. Интегрируем равенство
.
Док-во. Интегрируем равенство
![]() в пределах от
до
:
в пределах от
до
:
![]() .
Функция в левом интеграле имеет
первообразную
.
Функция в левом интеграле имеет
первообразную
![]() ,
по формуле Ньютона-Лейбница
,
по формуле Ньютона-Лейбница
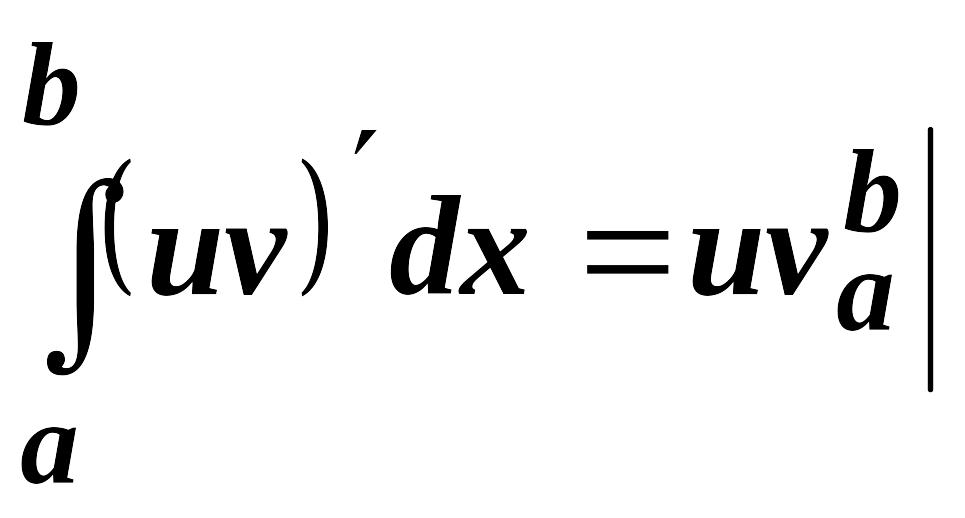 ,
следовательно,
,
следовательно,
![]() ,
откуда и следует доказываемое равенство.:
,
откуда и следует доказываемое равенство.:
![]() .
.
Замена
переменной в определённом интеграле.
Теорема. Пусть функция
![]() определена,
непрерывно дифференцируема и монотонна
на отрезке
определена,
непрерывно дифференцируема и монотонна
на отрезке
![]() ,
,![]() ,функция
непрерывна на отрезке
.
,функция
непрерывна на отрезке
.
Тогда
![]() .Док-во.
Пусть
- первообразная для функции
,
т.е.
.Док-во.
Пусть
- первообразная для функции
,
т.е.
![]() ,
тогда
,
тогда
![]() - первообразная для функции
- первообразная для функции
![]() .
.
![]() ,
что и требовалось доказать.
,
что и требовалось доказать.
При решении задач нельзя забывать о том, что при переходе к новой переменной надо обязательно вычислить новые пределы интеграла.
интегралы, для которых нарушаются эти требования (т.е. неограничена либо подынтегральная функция, либо область интегрирования, либо и то, и другое вместе) несобственными.
Определение
несобственного интеграла по бесконечному
промежутку. Пусть функция f(x) определена
на полуоси
![]() и интегрируема по любому отрезку [a,b],
принадлежащему этой полуоси. Предел
интеграла
и интегрируема по любому отрезку [a,b],
принадлежащему этой полуоси. Предел
интеграла
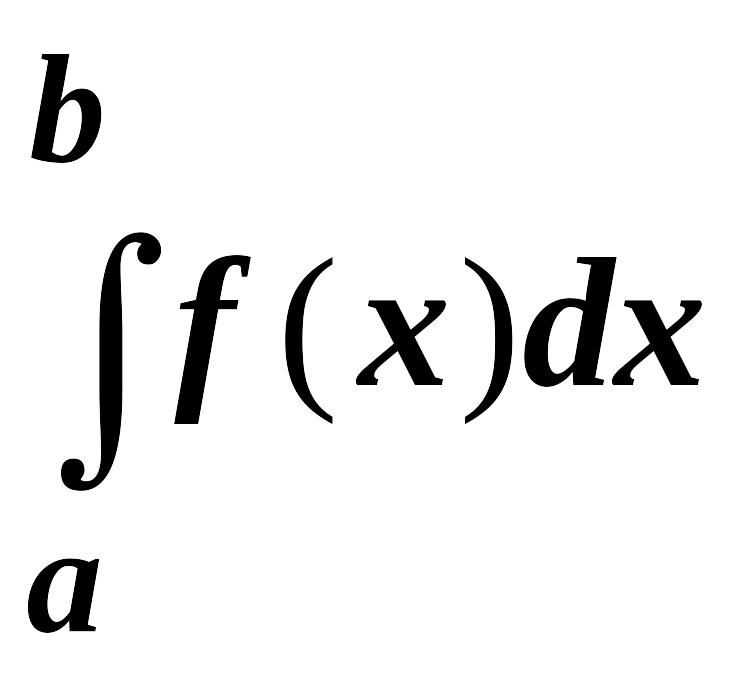 при
при
![]() называется несобственным интегралом
функции f(x) от a до
называется несобственным интегралом
функции f(x) от a до
![]() и обозначается
и обозначается
![]() .
.
Итак,
по определению,
![]() .
Если этот предел существует и конечен,
интеграл
называется сходящимся; если предел не
существует или бесконечен, интеграл
называется расходящимся.
.
Если этот предел существует и конечен,
интеграл
называется сходящимся; если предел не
существует или бесконечен, интеграл
называется расходящимся.
пр
сход Абеля: пусть функции f(x) и g(x)
определены в промежутке
![]() ,
причём 1. f(x) интегрируема в этом промежутке,
т.е. интеграл
,
причём 1. f(x) интегрируема в этом промежутке,
т.е. интеграл
![]() сходится (условно или абсолютно);
сходится (условно или абсолютно);
