34. Необходимый признак сходимости. Гармонический ряд.
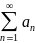(1)
Выполнение – не гарантирует сходимость ряда. Невыполнение – гарантирует расходимость.
Т1. Необх признак сходимости рядов.
Если ряд (1) сходится, то предел n-члена = 0.
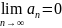
Док-во:
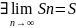
Sn-1=Sn-an
=>
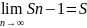
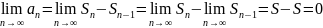
Т2. Достаточный признак сходимости
Если
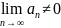=> (1) – расходится
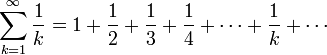гармонический
ряд, расходится
Докажем расходимость:
Доказательство расходимости можно построить, группируя слагаемые следующим образом:
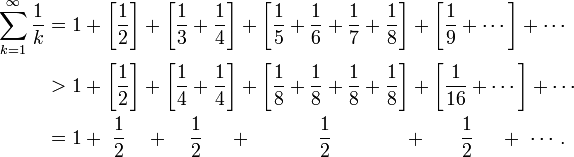
Последний ряд, очевидно, расходится.
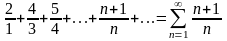
Для
этого ряда
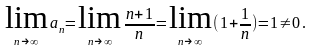
35. Признаки сравнения.
- знакоположит., если все an>0
(1)
и
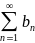(2) – эталонный, an,
bn
> 0, исследуем an
Т3. Непредельный признак сравнения.
1. если an < bn то при любых n (2) – cход => (1) сход
2. если an > bn то при любых n (2) – расх => (1) расх
замечание: в кач-ве ряда сравнения обычно выбирают:
а)
- обобщ. гармон. ряд (ряд Дерихле) – (сх
при a>1,
расх a≤1)
б)
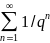(сх при |q|<1,
расх |q|≥1)
Т4. Предельный признак сравнения.
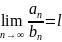
а) 0≤l≤∞ (2) – сх => (1) – сх.
б) ∞≥l≥∞ (2) – расх => (1) – расх
в) 0<l<∞ (2 и 1) – сх или расх одновременно – применять другие признаки
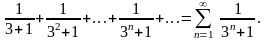
Члены ряда положительны и меньше соответствующих членов сходящегося ряда геометрической прогрессии
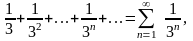т.
к.
,
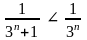n=1,2,…
Следовательно, по признаку сравнения исходный ряд также сходится.
36. Признак Даламбера.
Пусть члены положительного ряда (1.1) таковы, что существует предел
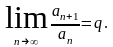
Тогда: 1) при q < 1 ряд (1.1) сходится;
2) при q > 1 ряд (1.1) расходится;
3) при q = 1 о сходимости ряда (1.1) ничего сказать нельзя, необходимы дополнительные исследования.
док-во:
При
выбираем
так, чтобы
.
Пусть
выбрано так, чтобы при
, т.е.
и
,
.
По предыдущей теореме ряд сходится.
Если же
,
то выберем
так, что
.
Тогда при
и ряд расходится.
37. Радикальный и интегральный признак Коши.
Радикальный: Пусть члены положительного ряда (1.1) таковы, что существует предел
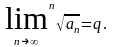
Тогда: 1) при q < 1 ряд (1.1) сходится;
2) при q > 1 ряд (1.1) расходится;
3) при q = 1 о сходимости ряда (1.1) ничего сказать нельзя, необходимы дополнительные исследования.
Д-во: в точности повторяет док-во признака даламбера.
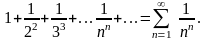
Применим предельный признак Коши:
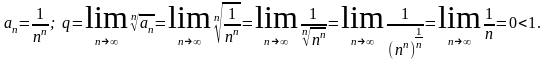
Следовательно, исходный ряд сходится.
Интегральный:
Пусть
функция f(x)
непрерывная неотрицательная невозрастающая
функция на промежутке
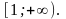
Тогда
ряд
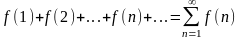и несобственный интеграл
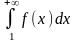сходятся или расходятся одновременно.
|
|
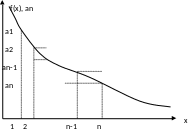
Доказательство.
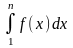- это площадь под графиком функции
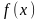при
.
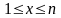Так
как
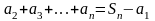(сумма площадей прямоугольников)
ограничивает площадь под графиком
функции снизу, а
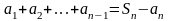ограничивает ее сверху, то
.
.
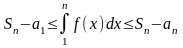Достаточность.
Если
интеграл сходится, то
,
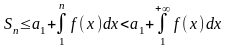поэтому последовательность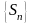
ограничена сверху. Так как эта
последовательность не убывает, то по
теореме Вейерштрасса
.
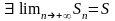Поэтому ряд
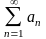сходится.
Необходимость.
Если ряд
сходится,
то
,
а по необходимому признаку сходимости
ряда
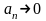при
.
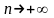Поэтому последовательность
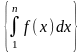(неубывающая,
так как
)
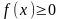ограничена сверху. Следовательно, по
теореме Вейерштрасса
,
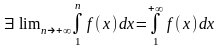т.е. несобственный интеграл сходится.
Если ряд расходится, то и интеграл расходится и наоборот. Это легко доказывается от противного.
Применим интегральный признак Коши.
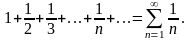
В
нашем случае функция
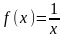удовлетворяет условию теоремы. Исследуем
на сходимость несобственный интеграл
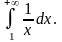
Имеем
.
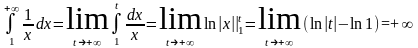Несобственный интеграл расходится, следовательно, исходный гармонический ряд расходится также.