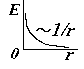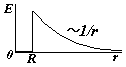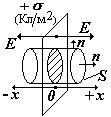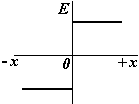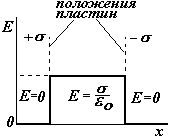Тема 2. Вопрос 2.
Теорема Гаусса.
|
при дискретном распределении зарядов |
Теорема Гаусса: «Поток вектора напряженности через любую замкнутую поверхность равен алгебраической сумме зарядов, охватываемых этой поверхностью, деленной на о» (о – электрическая постоянная)
|
|
при непрерывном распределении зарядов |
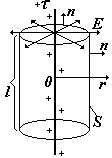
2)Тонкая длинная нить, заряженная с линейной плотностью заряда (Кл/м)
В этом случае «гауссова» поверхность – соосный с нитью цилиндр длиной l.
Сначала найдем поток, потом воспользуемся теоремой Гаусса.
|
Разобьем поверхность цилиндра на боковую и две торцевых. Для боковой cos = 1, для торцевых cos = 0. |
|
|
по теореме Гаусса; охватываемый заряд – это отрезок нити длиной l. Приравнивая и сокращая, получим E(r). |
|
|
||
|
Тема 2. Вопрос 3.
Теорема Гаусса.
|
при дискретном распределении зарядов |
Теорема Гаусса: «Поток вектора напряженности через любую замкнутую поверхность равен алгебраической сумме зарядов, охватываемых этой поверхностью, деленной на о» (о – электрическая постоянная)
|
|
при непрерывном распределении зарядов |
3) Тонкостенный длинный цилиндр, заряженный:
с линейной плотностью заряда или
с поверхностной плотностью заряда .
Этот пример аналогичен предыдущему. Выбираем гауссову поверхность в виде соосного цилиндра, разбиваем поверхность на боковую и две торциальные. В первом случае при заданной линейной плотности получим такую же формулу, как идля длинной нити. Во втором случае охватываемый заряд равен (2Rl) и формула для E несколько иная, хотя зависимость от r – та же.
|
|
|
Тема 2. Вопрос 4.
Теорема Гаусса.
|
при дискретном распределении зарядов |
Теорема Гаусса: «Поток вектора напряженности через любую замкнутую поверхность равен алгебраической сумме зарядов, охватываемых этой поверхностью, деленной на о» (о – электрическая постоянная)
|
|
при непрерывном распределении зарядов |
4) Плоскость, бесконечно протяженная, заряженная с поверхностной плотностью заряда .
Выберем гауссову поверхность S в виде цилиндра, перпендикулярного заряженной плоскости. Высота цилиндра (2х/2). Разобьем поверхность на боковую и две торцевых.
|
поток через Sбок = 0, т.к. En, = 90о и cos = 0 |
|
|
|
Sзаштрих – площадка с зарядом, охватываемым цилиндром |
||
|
|||
|
S заштрих = S торц, т.к. образующие цилиндра перпендикулярны заряженной плоскости. Поле протяженной плоскости – однородное и не зависит от расстояния |
||
5) Две плоскости, параллельные, разноименно заряженные (плоский конденсатор). В этом случае напряженность поля можно найти по принципу суперпозиции, зная напряженность поля одной плоскости:
|
|
|
|
||
Поле плоского конденсатора можно считать однородным с достаточной степенью точности, если расстояние между пластинами значительно больше размеров пластин. |
||
