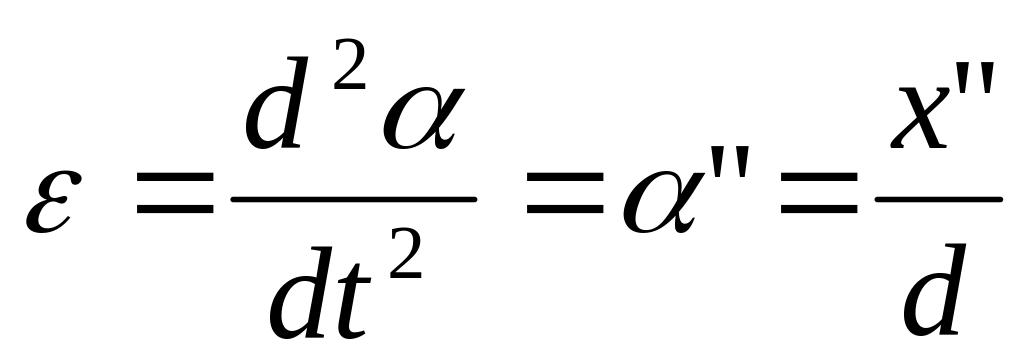- •Тема 1. Вопрос 1.
- •Тема 1. Вопрос 2.
- •Тема 1. Вопрос 3.
- •Тема 1. Вопрос 4.
- •Тема 1. Вопрос 5.
- •Тема 1. Вопрос 6.
- •Тема 2. Вопрос 1.
- •Тема 2. Вопрос 2.
- •Тема 2. Вопрос 3.
- •Тема 2. Вопрос 4.
- •Тема 3. Вопрос 1.
- •1) Точечный заряд.
- •Тема 3. Вопрос 2.
- •Тема 3. Вопрос 3.
- •Тема 3. Вопрос 4.
- •Тема 4. Вопрос 1.
- •Тема 4. Вопрос 2.
- •Тема 4. Вопрос 3.
- •Тема 5. Вопрос 1.
- •Тема 5. Вопрос 2.
- •Тема 5. Вопрос 3.
- •Тема 5. Вопрос 4.
- •Тема 5. Вопрос 5.
- •Тема 6. Вопрос 1.
- •Тема 6. Вопрос 2.
- •Тема 6. Вопрос 3.
- •Тема 6. Вопрос 4.
- •Тема 6. Вопрос 5.
- •Часть 1.
- •Тема 6. Вопрос 5.
- •Часть 2.
- •Тема 7. Вопрос 1.
- •2) Система n точечных дискретных зарядов.
- •Тема 7. Вопрос 2.
- •3) Заряженный проводник.
- •4) Заряженный конденсатор.
- •Тема 7. Вопрос 3.
- •Тема 8. Вопрос 1.
- •Тема 8. Часть 1. Вопрос 1.
- •Тема 8. Часть 2. Вопрос 1.
- •Тема 8. Вопрос 3.
- •Часть 1.
- •Тема 8. Вопрос 3.
- •Часть 2.
- •Тема 8. Вопрос 4.
- •Тема 8. Вопрос 5.
- •Тема 9. Вопрос 1.
- •Часть 1.
- •Тема 9. Вопрос 1.
- •Часть 2.
- •Тема 9. Вопрос 2.
- •Тема 9. Вопрос 3.
- •Тема 9. Вопрос 4.
- •1)Магнитное поле прямого проводника конечной длины.
- •2)Магнитное поле прямого бесконечно длинного проводника.
- •Тема 9. Вопрос 5.
- •3)Магнитное поле на оси кругового тока.
- •4) Магнитное поле в центре кругового тока
- •Тема 9. Вопрос 6.
- •1) Прямой бесконечный проводник с током.
- •Тема 9. Вопрос 7.
- •2) Индукция магнитного поля внутри длинного соленоида.
- •Тема 9. Вопрос 8.
- •Тема 10. Вопрос 1.
- •Тема 10. Вопрос 2.
- •Тема 10. Вопрос 3.
- •Тема 10. Вопрос 4.
- •1) Однородное поле.
- •2) Неоднородное поле.
- •Тема 10. Вопрос 5.
- •Тема 11. Вопрос 1.
- •Тема 11. Вопрос 2.
- •Тема 11. Вопрос 3.
- •Тема 11. Вопрос 4.
- •Тема 12. Вопрос 1.
- •Тема 13. Вопрос 1.
- •Тема 13. Вопрос 2.
- •Тема 13. Вопрос 3.
- •Тема 13. Вопрос 4.
- •Тема 14. Вопрос 1.
- •Тема 14. Вопрос 2.
- •Тема 14. Вопрос 3.
- •Тема 15. Вопрос 1.
- •Тема 15. Вопрос 2.
- •Тема 15. Вопрос 3.
- •Тема 15. Вопрос 4.
- •Тема 15. Вопрос 5.
- •Тема 15. Вопрос 6.
- •Тема 16. Вопрос 1.
- •Часть 1.
- •Тема 16. Вопрос 1.
- •Часть 2.
- •Тема 16. Вопрос 2.
- •Тема 17. Вопрос 1.
- •Тема 17. Вопрос 2.
- •Тема 18. Вопрос 1.
- •Тема 18. Вопрос 2.
- •Тема 18. Вопрос 3.
Тема 15. Вопрос 3.
Математический
маятник.
Это тело, подвешенное на легкой нити,
размерами которого можно пренебречь
по сравнению с длиной нити. Запишем II
закон Ньютона в проекции на касательное
к траектории (окружности) направление:
ma,=
- mg
sin(a),
![]() -
тангенциальное
ускорение. Это уравнение является
уравнением колебаний, но не гармонических
и имеет более сложно решение, чем
.
Мы рассмотрим только случай малых углов
α.
При малых углах sin(a)
≡ a
≡ x/l,где
l-длина
нити.
-
тангенциальное
ускорение. Это уравнение является
уравнением колебаний, но не гармонических
и имеет более сложно решение, чем
.
Мы рассмотрим только случай малых углов
α.
При малых углах sin(a)
≡ a
≡ x/l,где
l-длина
нити.
|
II закон Ньютона; сравнивая c , найдем циклическую частоту и период колебаний.
|
|
В данном случае возвращающая сила - это составляющая силы тяжести, т.е. сила гравитационной природы, а т.к. при малых углах она пропорциональна смещению, ее можно назвать квазиупругой. |
||
Тема 15. Вопрос 4.
Физический маятник. Это любое твердое тело, способное совершать колебания относительно неподвижной точки, не совпадающей с его центром тяжести. Если маятник отклонить от положения равновесия, то возникнет возвращающий момент, создаваемый составляющей силы тяжести mg∙sin(α)и равный mg∙sin(a)∙d, где d- плечо силы (см. рис.). Данное тело может совершать только вращательное движение, поэтому II закон Ньютона будет иметь вид: Iε = -mgd; где I - момент инерции тела, а ε - угловое ускорение. Это уравнение колебаний, но не гармонических. Однако при малых углах оно приобретает вид , т.е. дифференциального уравнении гармонических колебаний. При малых углах sin(a) ≡ a ≡ x/d
d - расстояние от точка подвеса до центра тяжести.
угловое ускорение |
II закон Ньютона |
|
круговая частота и период колебаний физического маятника |
|
|
уравнение гармонических колебаний |
|
||
|
приведенная
длина физического маятника.
Если взять нить длиной
|
|||
Тема 15. Вопрос 5.
смещение точки от положения равновесия
скорость, колеблющейся точки и ее амплитуда (максимальное значение)
ускорение колеблющейся точки и его амплитуда (максимальное значение)