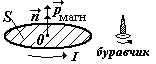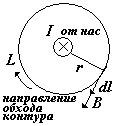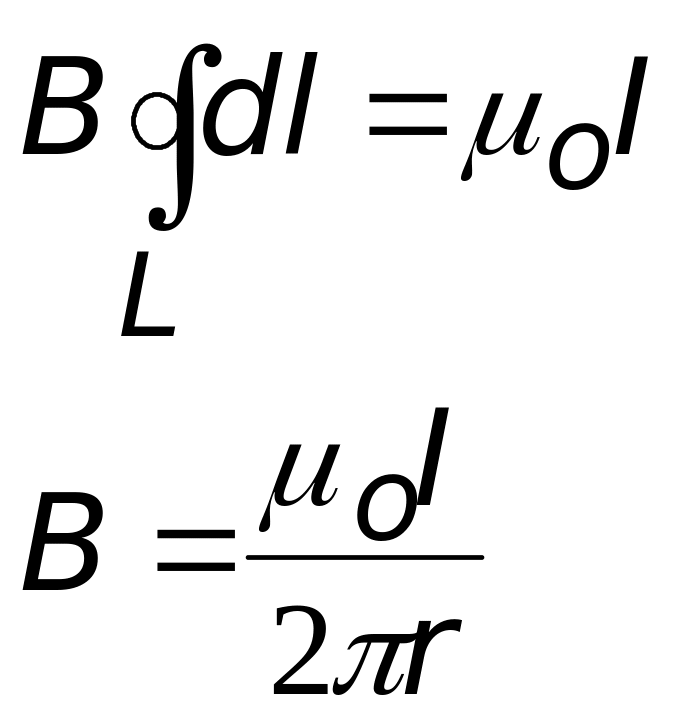- •Тема 1. Вопрос 1.
- •Тема 1. Вопрос 2.
- •Тема 1. Вопрос 3.
- •Тема 1. Вопрос 4.
- •Тема 1. Вопрос 5.
- •Тема 1. Вопрос 6.
- •Тема 2. Вопрос 1.
- •Тема 2. Вопрос 2.
- •Тема 2. Вопрос 3.
- •Тема 2. Вопрос 4.
- •Тема 3. Вопрос 1.
- •1) Точечный заряд.
- •Тема 3. Вопрос 2.
- •Тема 3. Вопрос 3.
- •Тема 3. Вопрос 4.
- •Тема 4. Вопрос 1.
- •Тема 4. Вопрос 2.
- •Тема 4. Вопрос 3.
- •Тема 5. Вопрос 1.
- •Тема 5. Вопрос 2.
- •Тема 5. Вопрос 3.
- •Тема 5. Вопрос 4.
- •Тема 5. Вопрос 5.
- •Тема 6. Вопрос 1.
- •Тема 6. Вопрос 2.
- •Тема 6. Вопрос 3.
- •Тема 6. Вопрос 4.
- •Тема 6. Вопрос 5.
- •Часть 1.
- •Тема 6. Вопрос 5.
- •Часть 2.
- •Тема 7. Вопрос 1.
- •2) Система n точечных дискретных зарядов.
- •Тема 7. Вопрос 2.
- •3) Заряженный проводник.
- •4) Заряженный конденсатор.
- •Тема 7. Вопрос 3.
- •Тема 8. Вопрос 1.
- •Тема 8. Часть 1. Вопрос 1.
- •Тема 8. Часть 2. Вопрос 1.
- •Тема 8. Вопрос 3.
- •Часть 1.
- •Тема 8. Вопрос 3.
- •Часть 2.
- •Тема 8. Вопрос 4.
- •Тема 8. Вопрос 5.
- •Тема 9. Вопрос 1.
- •Часть 1.
- •Тема 9. Вопрос 1.
- •Часть 2.
- •Тема 9. Вопрос 2.
- •Тема 9. Вопрос 3.
- •Тема 9. Вопрос 4.
- •1)Магнитное поле прямого проводника конечной длины.
- •2)Магнитное поле прямого бесконечно длинного проводника.
- •Тема 9. Вопрос 5.
- •3)Магнитное поле на оси кругового тока.
- •4) Магнитное поле в центре кругового тока
- •Тема 9. Вопрос 6.
- •1) Прямой бесконечный проводник с током.
- •Тема 9. Вопрос 7.
- •2) Индукция магнитного поля внутри длинного соленоида.
- •Тема 9. Вопрос 8.
- •Тема 10. Вопрос 1.
- •Тема 10. Вопрос 2.
- •Тема 10. Вопрос 3.
- •Тема 10. Вопрос 4.
- •1) Однородное поле.
- •2) Неоднородное поле.
- •Тема 10. Вопрос 5.
- •Тема 11. Вопрос 1.
- •Тема 11. Вопрос 2.
- •Тема 11. Вопрос 3.
- •Тема 11. Вопрос 4.
- •Тема 12. Вопрос 1.
- •Тема 13. Вопрос 1.
- •Тема 13. Вопрос 2.
- •Тема 13. Вопрос 3.
- •Тема 13. Вопрос 4.
- •Тема 14. Вопрос 1.
- •Тема 14. Вопрос 2.
- •Тема 14. Вопрос 3.
- •Тема 15. Вопрос 1.
- •Тема 15. Вопрос 2.
- •Тема 15. Вопрос 3.
- •Тема 15. Вопрос 4.
- •Тема 15. Вопрос 5.
- •Тема 15. Вопрос 6.
- •Тема 16. Вопрос 1.
- •Часть 1.
- •Тема 16. Вопрос 1.
- •Часть 2.
- •Тема 16. Вопрос 2.
- •Тема 17. Вопрос 1.
- •Тема 17. Вопрос 2.
- •Тема 18. Вопрос 1.
- •Тема 18. Вопрос 2.
- •Тема 18. Вопрос 3.
4) Магнитное поле в центре кругового тока
Это частный случай предыдущего примера, когда х = 0
|
Магнитная индукция в центре кругового тока |
|
Магнитный момент контура с током.
Контур с током (виток с током) при изучении магнитных свойств вещества имеет такое же значение, как диполь при изучении электрических свойств вещества. Рассматривая поведение витка с током во внешнем магнитном поле, можно качественно объяснить намагниченность различных веществ. Контур с током характеризуют векторной величиной рмагн магнитным моментом.
|
магнитный момент контура с током I - сила тока в контуре, S – площадь, охватываемая контуром, n- нормаль к площади контура |
|
Тема 9. Вопрос 6.
Теорема о циркуляции вектора магнитной индукции.
|
Теорема о циркуляции вектора магнитной индукции: «Циркуляция вектора индукции магнитного поля по любому замкнутому контуру L равна алгебраической сумме токов, охватываемых этим контуром, умноженной на o». |
|
Выражение () применяется в случаях дискретного распределения проводников с токами, т.е. когда имеются отдельные проводники с токами и требуется найти индукцию В поля вне проводников. Выражение () используется в случаях, когда требуется найти индукцию В магнитного поля внутри проводника с током, т.е. при непрерывном распределении тока по проводнику.
1) Прямой бесконечный проводник с током.
При использовании теоремы о циркуляции, нужно выбрать такую замкнутую кривую (контур L), в каждой точке которой индукция В была бы одинаковой по величине. Тогда В можно будет вынести из-под интеграла. В случае прямого тока линии индукции – концентрические окружности, и выбрав одну из линий индукции в качестве контура L, получим Вl = Вcos = B(cos = 1) (см.рис.). Запишем
|
теорема о циркуляции вектора магнитной индукции |
|
|
вынесем В= const, интеграл даст 2 r; т.о. найдем индукцию магнитного поля длинного прямого тока более простым способом, чем по закону БСЛ |
Тема 9. Вопрос 7.
Теорема о циркуляции вектора магнитной индукции.
() |
Теорема о циркуляции вектора магнитной индукции: «Циркуляция вектора индукции магнитного поля по любому замкнутому контуру L равна алгебраической сумме токов, охватываемых этим контуром, умноженной на o». |
() |
Выражение () применяется в случаях дискретного распределения проводников с токами, т.е. когда имеются отдельные проводники с токами и требуется найти индукцию В поля вне проводников. Выражение () используется в случаях, когда требуется найти индукцию В магнитного поля внутри проводника с током, т.е. при непрерывном распределении тока по проводнику.